免费服务器搭建网站详细教程智能小程序开发平台
1、intellij idea安装R包ggplot2问题
在我上次解决图形显示问题后,发现安装ggplot2包时出现了问题,这在之前高版本中并没有出现问题,
install.packages('ggplot2')ERROR: lazy loading failed for package 'lifecycle'
* removing 'C:/Users/VICTUS/Documents/R/win-library/4.0/lifecycle'
Warning in install.packages("ggplot2") :installation of package ‘lifecycle’ had non-zero exit status
ERROR: dependency 'lifecycle' is not available for package 'gtable'
* removing 'C:/Users/VICTUS/Documents/R/win-library/4.0/gtable'
Warning in install.packages("ggplot2") :installation of package ‘gtable’ had non-zero exit status
ERROR: dependencies 'gtable', 'lifecycle' are not available for package 'ggplot2'
* removing 'C:/Users/VICTUS/Documents/R/win-library/4.0/ggplot2'
Warning in install.packages("ggplot2") :installation of package ‘ggplot2’ had non-zero exit statusThe downloaded source packages are in‘C:\Users\VICTUS\AppData\Local\Temp\Rtmp6Hd81s\downloaded_packages’但是在高版本r语言中并没有出现此问题,为此:
为了使intellij idea显示图片,降级r语言,但是安装r包时候出现问题;
为了安装包不出问题,升级r语言版本,可是图像显示又出现了问题。
在查找了大量资料后发现这是两者接入的bug问题,官方仍在修复,所以为了舒适使用R语言编写代码,使用RStudio是不错的选择。
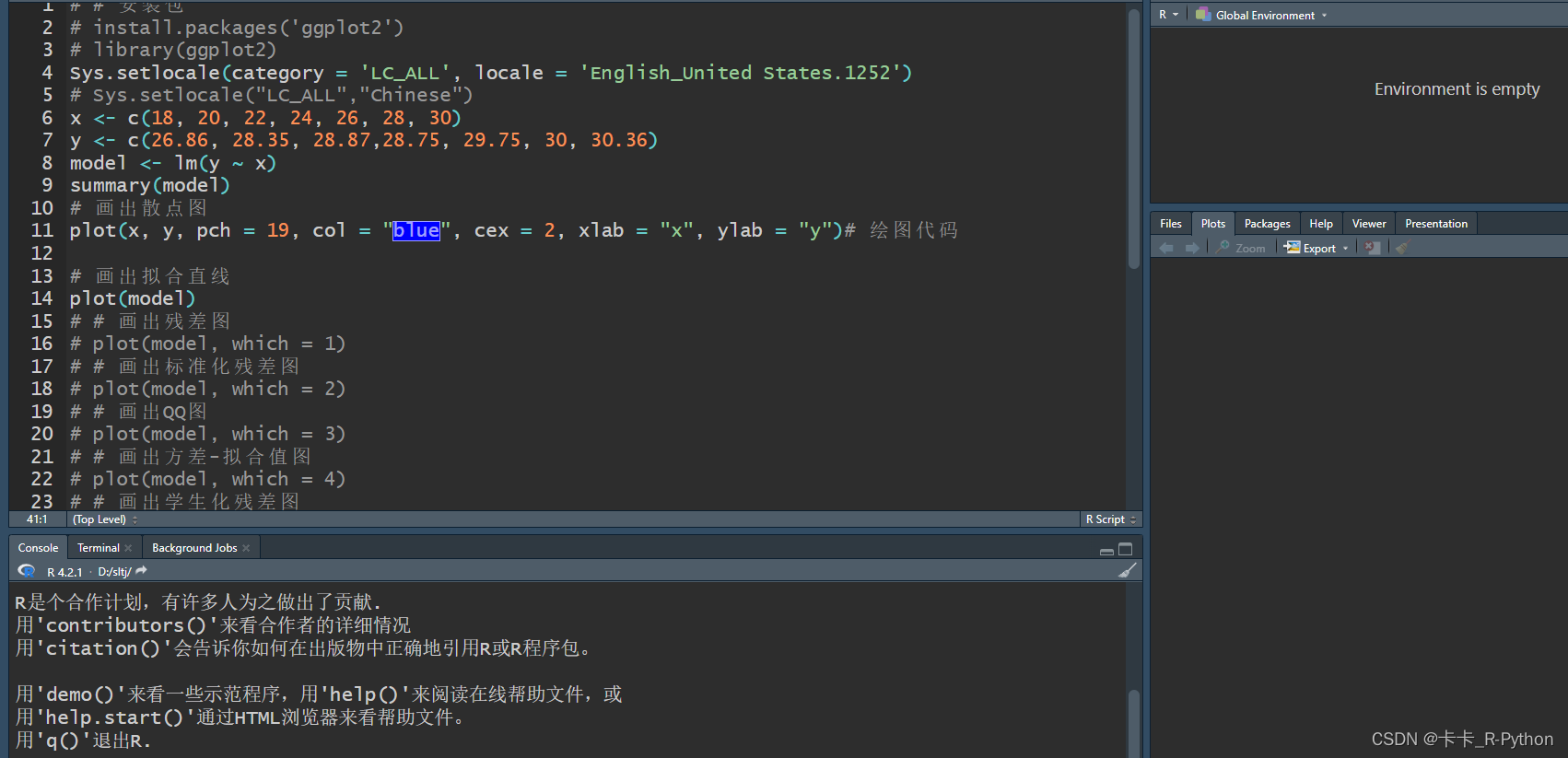
2、在RStudio中运行正常显示
在RStudio中打开文件,运行,发现一切正常。
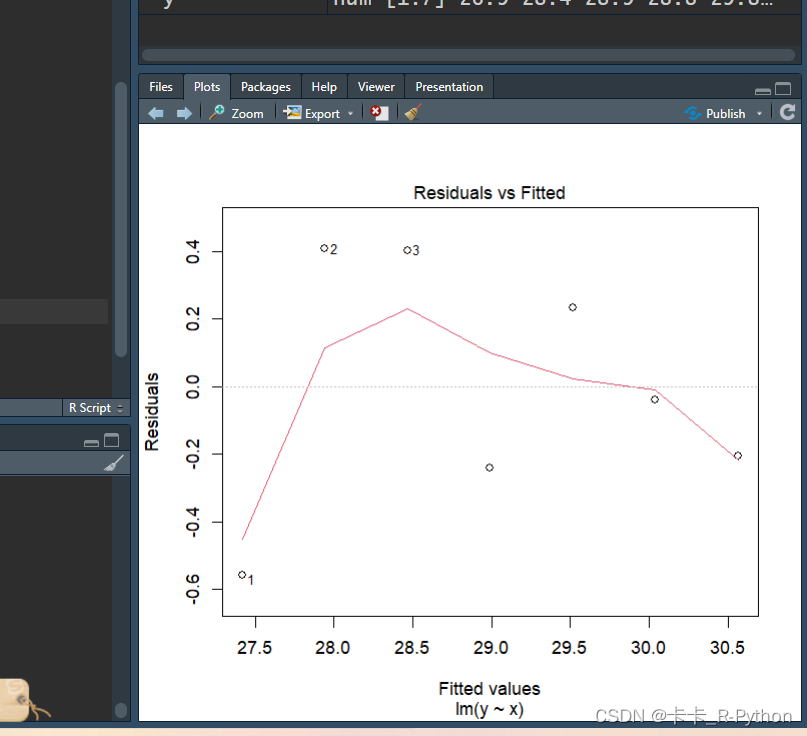
结果可以准确输出。
安装r包:
install.packages("pak")
可见r包也是正常安装。
所以,为了更好的r语言体验,使用RStudio进行编写可以很好的避免上述问题。
