做数学ppt工具的网站wordpress输入密码访问
说明:这是一个机器学习实战项目(附带数据+代码+文档),如需数据+代码+文档可以直接到文章最后关注获取。


1.项目背景
在当今的大数据时代,面对海量且维度极高的数据集,如何高效地进行特征选择成为了提升机器学习模型性能的关键挑战之一。传统BP神经网络虽然在处理非线性分类问题上展现出强大能力,但其对初始权重敏感、易陷入局部最优解等缺点限制了其应用效果。为解决这些问题,本项目引入HPSO_TVAC(混合粒子群优化算法结合时变加速度系数),通过其强大的全局搜索能力来优化BP神经网络的输入特征选择过程。这种组合不仅有助于克服BP神经网络固有的局限性,还能显著提高分类精度和模型泛化能力。基于Python平台实现这一方法研究,旨在探索一种更有效的特征选择策略,为复杂数据环境下的模式识别与智能决策提供新的解决方案,具有重要的理论意义和广泛的应用前景。
本项目通过基于HPSO_TVAC与BP神经网络分类模型的特征选择方法研究(Python实现)。
2.数据获取
本次建模数据来源于网络(本项目撰写人整理而成),数据项统计如下:
| 编号 | 变量名称 | 描述 |
| 1 | x1 | |
| 2 | x2 | |
| 3 | x3 | |
| 4 | x4 | |
| 5 | x5 | |
| 6 | x6 | |
| 7 | x7 | |
| 8 | x8 | |
| 9 | x9 | |
| 10 | x10 | |
| 11 | x11 | |
| 12 | x12 | |
| 13 | x13 | |
| 14 | x14 | |
| 15 | x15 | |
| 16 | x16 | |
| 17 | x17 | |
| 18 | x18 | |
| 19 | x19 | |
| 20 | x20 | |
| 21 | x21 | |
| 22 | x22 | |
| 23 | x23 | |
| 24 | x24 | |
| 25 | x25 | |
| 26 | x26 | |
| 27 | x27 | |
| 28 | x28 | |
| 29 | x29 | |
| 30 | x30 | |
| 31 | y | 因变量 |
数据详情如下(部分展示):

3.数据预处理
3.1 用Pandas工具查看数据
使用Pandas工具的head()方法查看前五行数据:

关键代码:

3.2数据缺失查看
使用Pandas工具的info()方法查看数据信息:


从上图可以看到,总共有31个变量,数据中无缺失值,共2000条数据。
关键代码:

3.3数据描述性统计
通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

关键代码如下:

4.探索性数据分析
4.1 y变量柱状图
用Matplotlib工具的plot()方法绘制柱状图:

4.2 y=1样本x1变量分布直方图
用Matplotlib工具的hist()方法绘制直方图:

4.3 相关性分析

部分数据变量的相关性分析:从上图中可以看到,数值越大相关性越强,正值是正相关、负值是负相关。
5.特征工程
5.1 建立特征数据和标签数据
关键代码如下:

5.2 数据集拆分
通过train_test_split()方法按照80%训练集、20%验证集进行划分,关键代码如下:

6.构建特征选择模型
主要通过基于HPSO_TVAC与BP神经网络分类模型的特征选择方法研究(Python实现)。
6.1 寻找最优特征
最优特征值:

6.2 最优特征构建模型
这里通过最优特征构建分类模型。
| 模型名称 | 模型参数 |
| BP神经网络分类模型 | units=32 |
| optimizer =opt = tf.keras.optimizers.Adam(learning_rate=0.01) | |
| epochs=50 |
6.3 模型摘要信息

6.4 模型训练集测试集准确率和损失曲线图
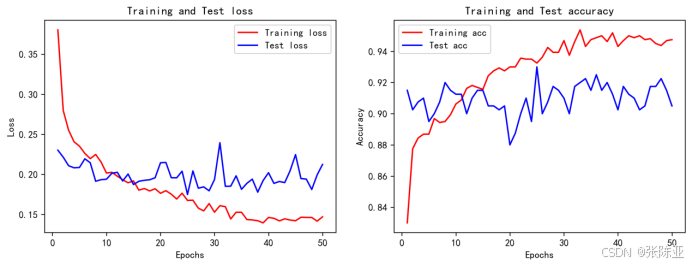
7.模型评估
7.1评估指标及结果
评估指标主要包括准确率、查准率、查全率、F1分值等等。
| 模型名称 | 指标名称 | 指标值 |
| 测试集 | ||
| BP神经网络分类模型 | 准确率 | 0.9050 |
| 查准率 | 0.8732 | |
| 查全率 | 0.9372 | |
| F1分值 | 0.904 | |
从上表可以看出,F1分值为0.904,说明模型效果良好。
关键代码如下:

7.2 分类报告

从上图可以看出,分类为0的F1分值为0.91;分类为1的F1分值为0.90。
7.3 混淆矩阵

从上图可以看出,实际为0预测不为0的 有26个样本,实际为1预测不为1的 有12个样本,模型效果良好。
8.结论与展望
综上所述,本文采用了通过基于HPSO_TVAC与BP神经网络分类模型的特征选择方法研究(Python实现),最终证明了我们提出的模型效果良好。此模型可用于日常产品的建模工作。
