网站开发的毕业设计论文框架浙江城乡住房建设厅网站
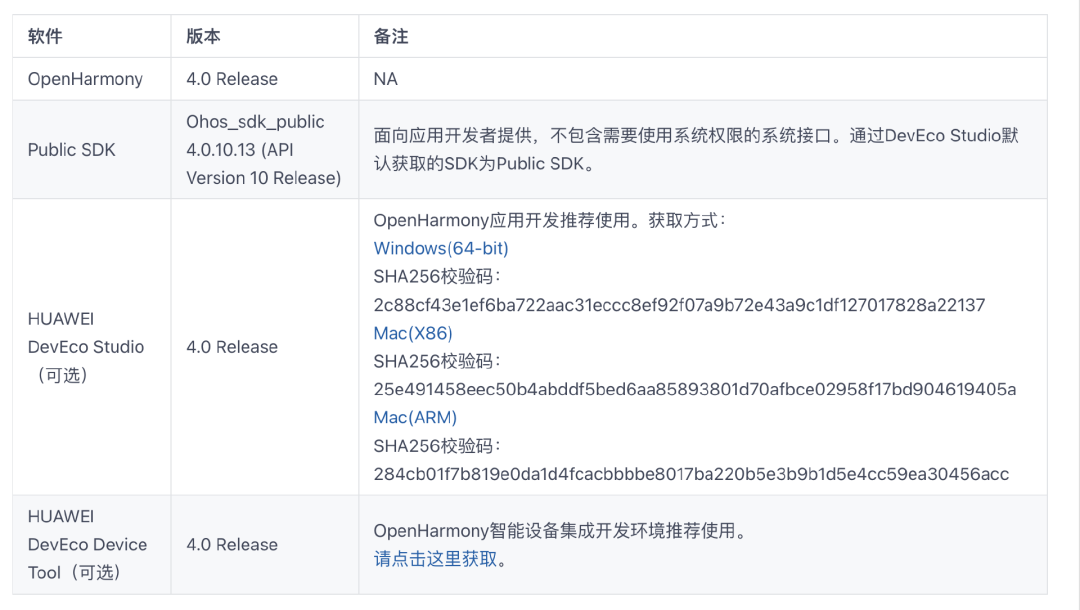
OpenHarmony的应用开发工具HUAWEI DevEco Studio现在随着OpenHarmony版本发布而发布,只能在版本发布说明中下载,例如最新版本的OpenHarmony 4.0 Release。对应的需要下载DevEco Studio 4.0 Release,如下图。
图片
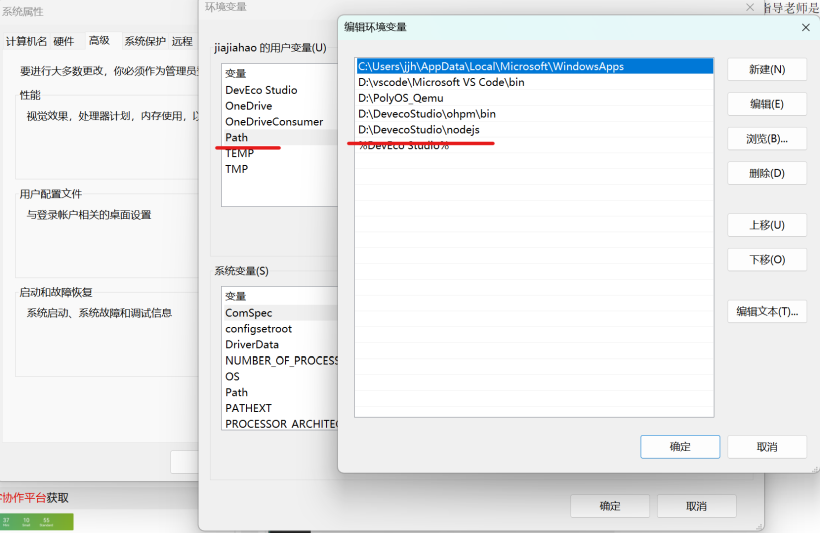
下载Full SDK主要有两种方式,一种是通过DevEco Studio下载好nodejs,配置npm为全局变量;另一种是OpenHarmony数字协作平台获取。对于第一种不过多说明:
图片
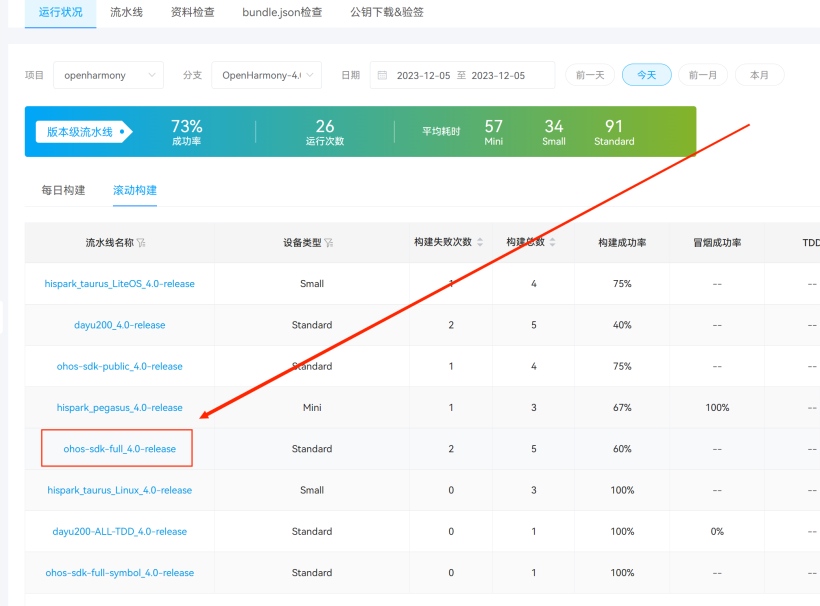
第二种是使用OpenHarmony数字协作平台获取。首先,需要到OpenHarmony数字协作平台 下载Full SDK,如下图。
图片
下载好后,分别解压出ets js native previewer toolchains,把它们一起放在DevEco Studio中设置的sdk目录下&#
