广州市公司网站建设公司怎么查看网站是否做静态化处理
电子钟的制作
一、课程设计目的
综合组合逻辑电路和时序逻辑电路知识,设计一个电子钟,电路功能要求如下:
(1)二十四/十二制小时、分、秒计时。采用七段数码管显示,由七段字形译码器驱动;
(2)小时、分钟可以校正(顺时针校正);
(3)使用小时及分钟完成定时闹钟功能,到达指定时间几时几分后,led灯闪烁1分。
(4)时分秒显示、小时制式选择、校正按钮、闹铃设置及led灯要设计在主电路图中。
二、课程设计环境
Logisim V2.7.1
三、课程设计步骤
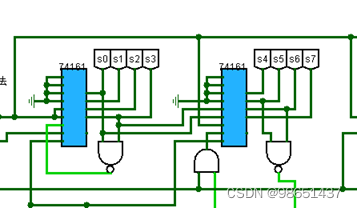
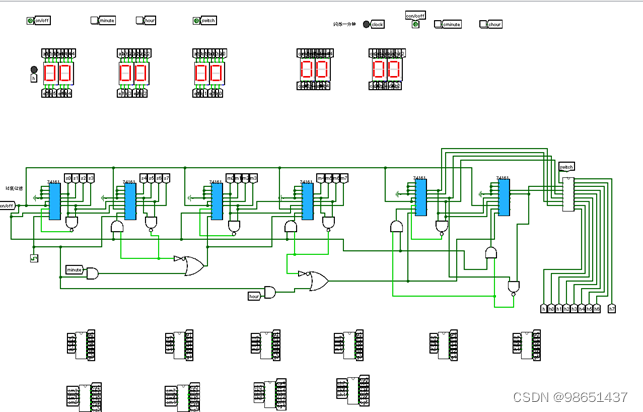
1.74161的实现
74HC161有清零,预置数,计数和保持功能

74161功能表
- 清零。Cr端为清零端。Cr=0,各触发器均被清零,计数器输出Q3Q2Q1Q0=0000。不清零时应使Cr=1。
- 预置数。Ld为预置数端。在Ld=0的前提下,加入CP脉冲上升沿,计数器将被预置数,即计数器输出Q3Q2Q1Q0等于D3D2D1D0输入的二进制数。这就可以使 计数器从预置数开始进行加法计数。不预置数时应使Ld=1。
- 计数。P=T=1(Cr=1,Ld=1)时,计数器处于工作状态。当计数器到Q3Q2Q1Q0=1111时,进位输出Qcc=1。再输入一个计数脉冲,计数器输出从1111返回到0000状态,Qcc由1变0,作为仅为输出信号。
- 保持。P=0,T=1(Cr=1,Ld=1)时,计数器处于保持状态。不仅计数器输出状态不变,而且进位输出状态不变。P=1,T=0(Cr=1,Ld=1)时,计数器输出状态保持不变,进位输出Qcc=0。

注:这玩意直接照搬课本上的,因为我自己不会设计74161.课本是数字逻辑与数字系统第6版,李景宏等著,电子工业出版社出版,(至少济大用这个)。
2.七段字形译码器的实现
有四个输入端A3A2A1A0,代表74161的四个输出。
其中0000到1001分别显示为0-9十个数字。a,b,c,d,e,f,g分别控制七个数字段。而多出的1010-1111部分全部输出0代表该数不存在。

7段字形译码器真值表
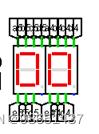
示例图

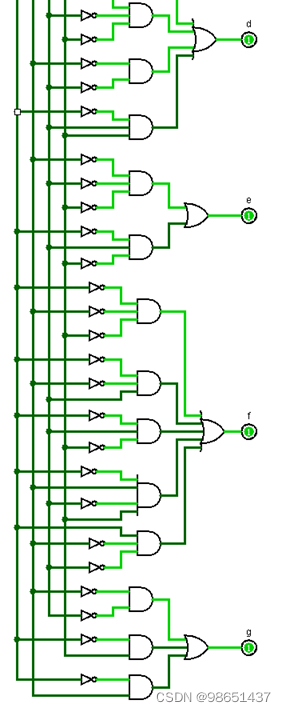
3.数值比较器的实现

数值比较器逻辑图

真值表
一位数值比较器,有三种情况:A>B,A=B,A<B。
其中输出A=B的逻辑结果,然后时钟的时间和闹钟的时间进行比较即可。
注:其实比较数值用与非门就行,为什么要搞这个,因为避免和同学雷同……
4.24进制的实现
采用Ld=0复位法。计数器为Q3Q2Q1Q0=1001时,个位到达9进位,给出与非的结果使Ld=0,送出0000预置数使个位为0,同时十位T,P信号为1,脉冲上升沿进位信号,十位进1.当个位为3,十位为2,即Q3Q2Q1Q0=0100时,与非门输出0给Ld复位。

24进制实现
5.60进制的实现
采用Ld=0复位法。计数器为Q3Q2Q1Q0=1001时,个位到达9进位,给出与非的结果使Ld=0,
送出0000预置数使个位为0,同时十位T,P信号为1,脉冲上升沿进位信号,十位进1.当个位为9,十位为5,即Q3Q2Q1Q0=0110时,与非门输出0给Ld复位,同时往时或分进位。
60进制实现
6.12/24小时进制切换的实现
Switch用来判断24,12的切换,默认0为24进制,1为12进制
a5,a4控制十位,a3a2a1a0控制个位。
当switch为0时,正常输出BCD8421码
当switch为1时,前12位正常输出,后面13-23转换为1-11输出。


24转12逻辑图



真值表
注:这玩意后面的超出范围可以不要,节省运行空间,老师是这么说的,但是我太懒了,没有去掉。
7.时、分、秒计时的实现
点击按钮打开时钟,秒钟开始运行,当秒钟到60时进行进位,然后分钟进位1.当分钟到60时进位,然后时钟进1.当时钟到24时进位清零,根据小时制切换。
与门用来清零。

时钟的设计
8.闹钟的实现
闹钟的时用24进制,分用60进制,然后时钟与闹钟每一位进行对比,如果全部符合则输出1,此时LED灯闪烁一分钟(只比较时和分),其中进制转换也要比较。

闹钟部分设计

闹钟提示设计
9.时间校正的实现
点击按钮与脉冲信号同样时,进行或运算,如果正常工作进位输出1,完成加一。代表这顺时
针校正。
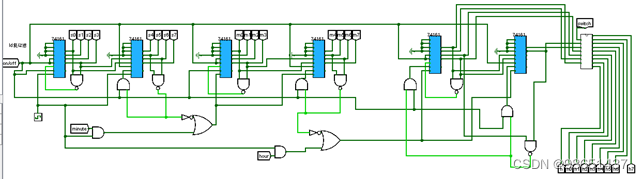
四、课程设计结果
电路总图

电路仿真结果图-时钟进位

进位前

进位后
电路仿真结果图-小时制切换
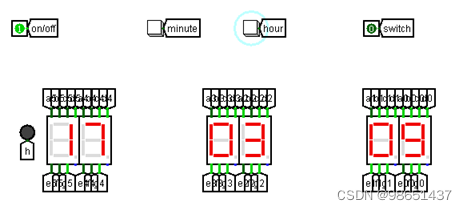
24小时制

12小时制(h代表切换提示)
电路仿真结果图-闹钟结果演示

闹钟前
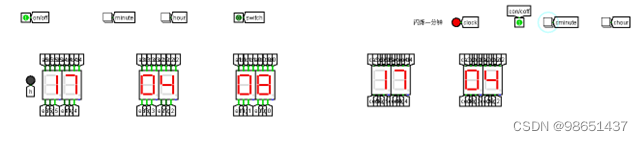
闹钟时

闹钟后
五、课程设计总结
1.部分借鉴了同学的思路,让我明白必要的合作是很有用的。
2.结合课本才能做出正确的电路设计。
3.这个是比较简单的电路设计了,但还是花了很长时间。
4.以后做这种设计一定要列出一个提纲。
5.适合济南大学的大一学生完成课程设计用,大概。
