网站seo的优化怎么做长沙网站建设专家
CentOS上安装Nginx:
1. 打开终端:使用SSH或者直接在服务器上打开终端。
2. 更新系统:运行以下命令以确保您的系统软件包列表是最新的:
sudo yum update
3. 安装Nginx:运行以下命令以安装Nginx:
sudo yum install nginx
4. 启动Nginx:安装完成后,运行以下命令以启动Nginx服务:
sudo systemctl start nginx
5. 设置Nginx开机启动:如果您希望Nginx在系统启动时自动启动,运行以下命令:
sudo systemctl enable nginx
6. 如果你是阿里云的服务器,你还需要去安全组里添加80端口访问的权限
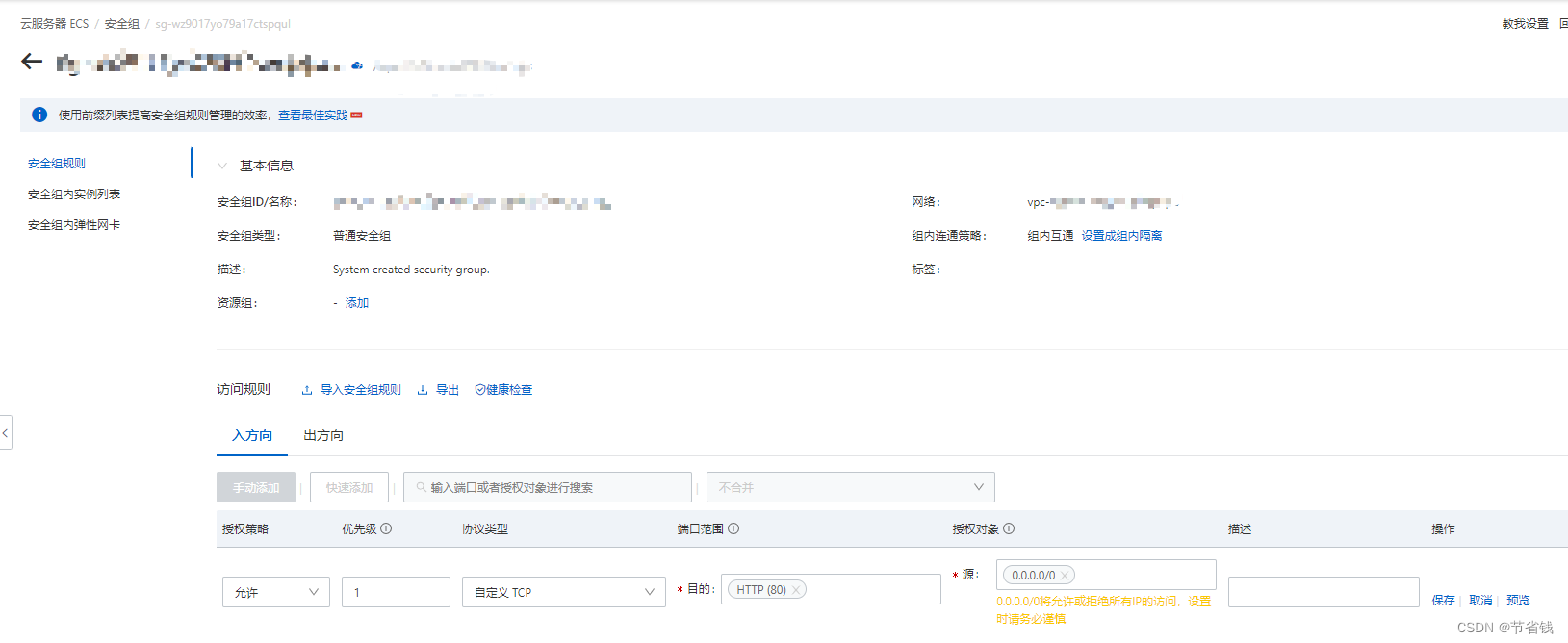
7. 验证Nginx安装:在浏览器中输入服务器的IP地址或域名,您应该能够看到Nginx的欢迎页面。
默认情况下,Nginx的配置文件位于/etc/nginx/nginx.conf。
这就是在CentOS上安装Nginx的基本步骤。安装完成后,您可以根据需要对Nginx的配置文件进行自定义,以满足您的特定需求。如果您想更详细地配置Nginx,可以编辑/etc/nginx/nginx.conf文件或在/etc/nginx/conf.d/目录中创建自定义配置文件。
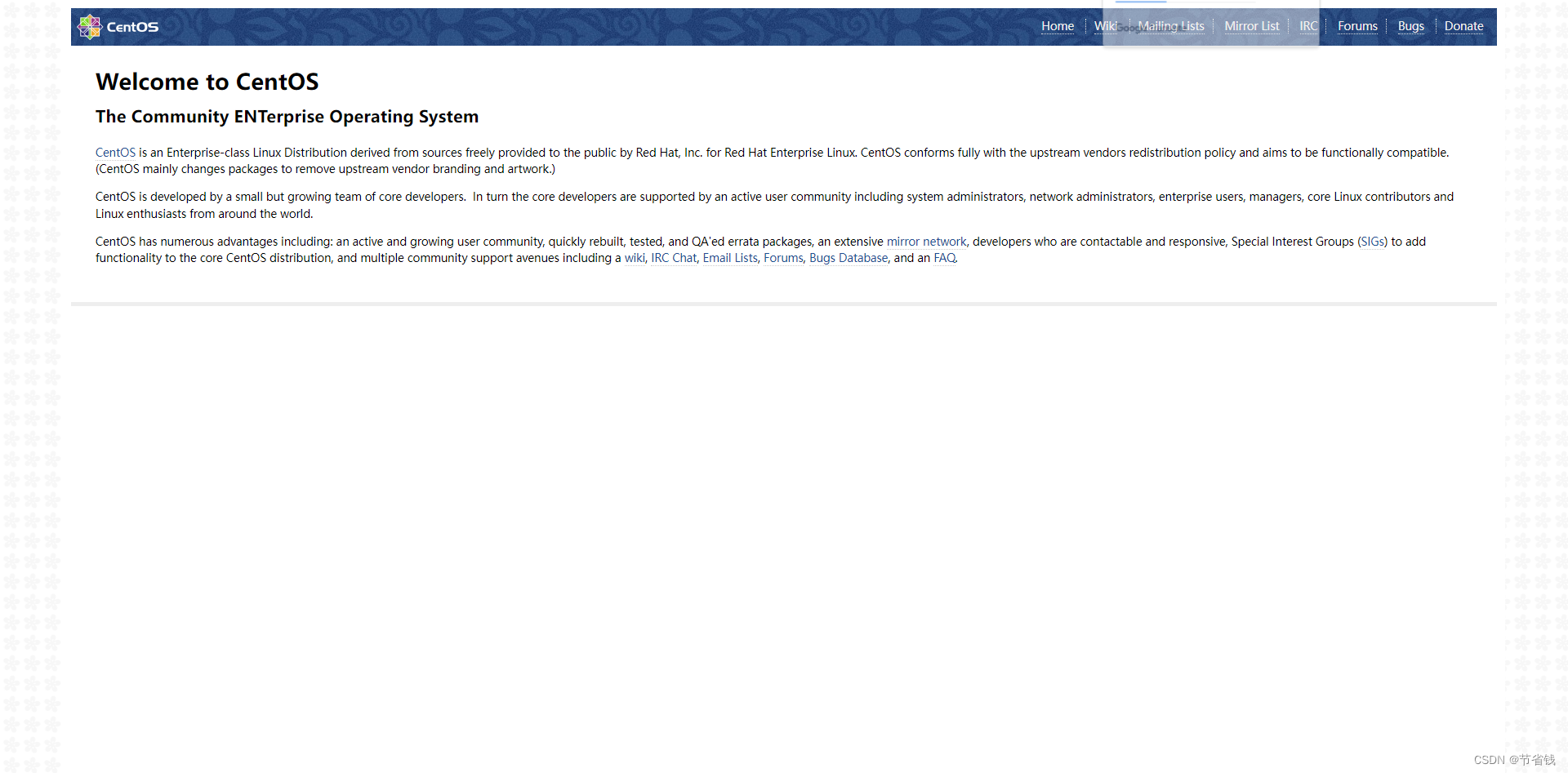
8.如果您使用防火墙(firewall),还需要确保允许HTTP流量通过。您可以使用以下命令来打开HTTP端口(80):
sudo firewall-cmd --permanent --add-service=http
sudo firewall-cmd --reload
这将允许HTTP流量通过防火墙。如果您需要启用HTTPS,您还需要打开HTTPS端口(443):
sudo firewall-cmd --permanent --add-service=https
sudo firewall-cmd --reload
如果报错 FirewallD is not running,请启动FirewallD
sudo systemctl start firewalld启用FirewallD以确保它在系统启动时自动启动:
sudo systemctl enable firewalld请确保在启动FirewallD之后再尝试运行sudo firewall-cmd命令以添加服务。如果FirewallD已启用并运行,但仍然遇到问题,可能需要查看FirewallD的日志以获取更多详细信息。您可以使用以下命令来查看FirewallD的日志:
sudo journalctl -u firewalld
这将显示FirewallD的日志,您可以检查是否有任何错误或警告消息。如果问题仍然存在,日志文件中的信息可能有助于进一步诊断问题。
