dede发布网站课程建设网站设计源码
爱剪辑
有开屏广告,一共3个界面:首页、剪同款、我的。
剪辑、配乐、字幕、滤镜、加速、贴纸、配音等主流功能都有。
特色功能有剪裁视频、倒放视频、视频旋转、视频转换GIF、转场、提取音频、画中画等。
还可以拼接视频,不过不支持FLV等小众文件格式。另外虽然支持多种比例拼接,但唯独缺少了按原始比例拼接。
遗憾的是,以上几乎所有功能都需要VIP才能导出,不然寸步难行。
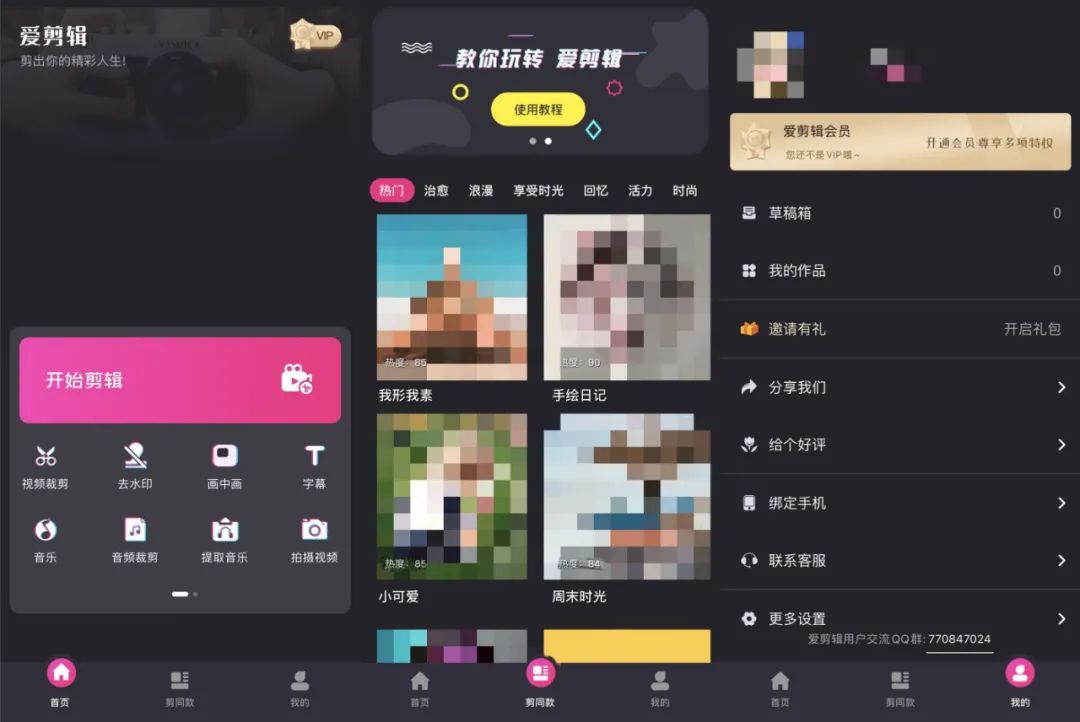
滤镜、贴纸、转场需要用到VIP的居多,导出无水印,但是超清导出也需要VIP,唯一的优点是导出视频无水印。
如果只需要随便把视频加工一下,不在乎精细剪辑,不希望有水印,可以用这款APP。
VN

模板很少,是一款偏向于自己有能力制作的APP,曲线变速、特效、变焦、滤镜、画中画、字幕、多段编辑、关键帧动画、定帧多种多样的编辑功能,更偏向专业的编辑。
优点:无水印导出,不小心删除的项目还可以在3天内在回收站中找回。缺点:模板少,不适合新手制作。
万兴喵影
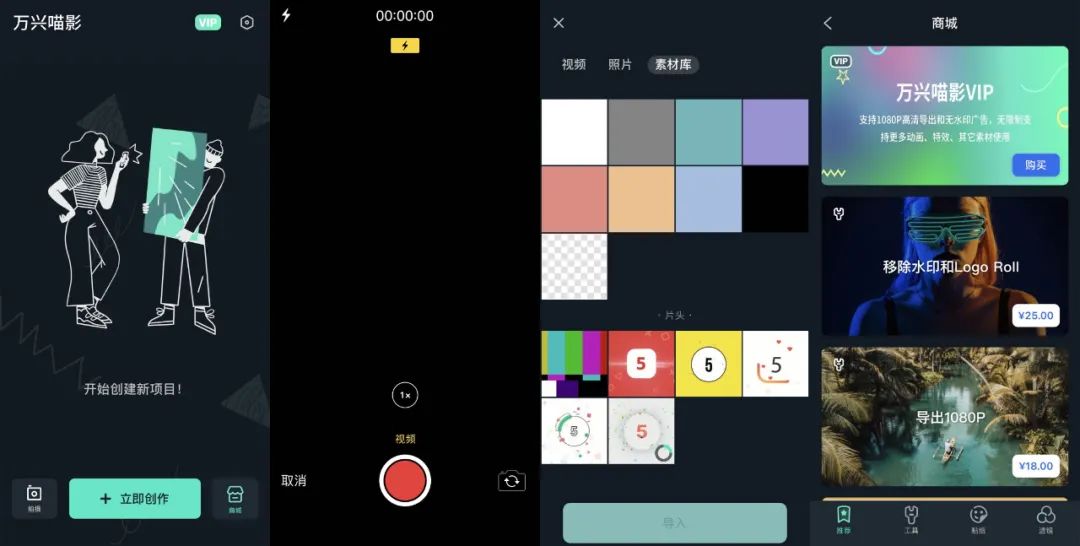
虽然有内置拍摄,但是不能拍照,只能录像。
“立即创作”中素材库少的可怜,一共就只有9张图片和6个片头。信息量最多的是商城,“推荐”“工具”“贴纸”“滤镜”分门别类,收费多少都标注的清清楚楚。
没有模板,不开VIP会有水印和片尾。有基础剪辑、片段编辑、视频变速、画中画、视频字幕、贴纸、音频、转场、滤镜、可调节参数。
该有的都有,但是素材太少,比如音乐只有24首,滤镜只有15个,特效只有12个。有个特色功能:提取音频,可以提取手机视频的音频到编辑中。
剪影
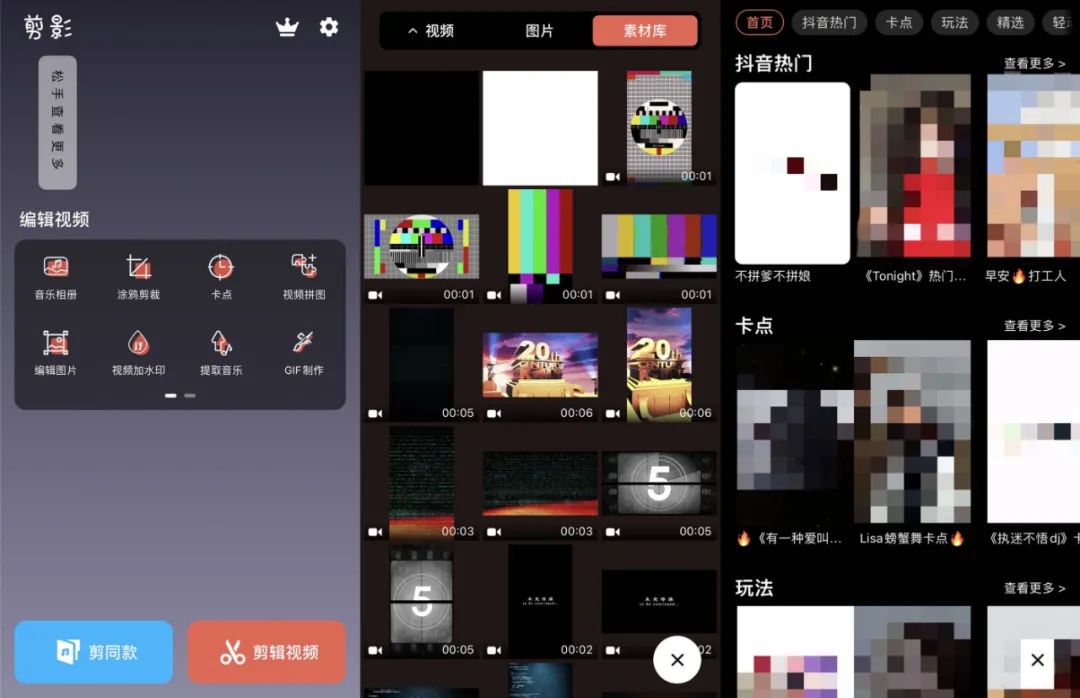
可以剪辑15分钟或更长时间的视频,基础剪辑、片段剪辑、提取音频、滤镜(支持美颜)、字幕、贴纸、特效、变速、可调节参数,需要的基础剪辑功能都有。
最大的优点是:自己剪辑出的视频导出无水印,提取音频可单独创作,提取出的音频可储存到文件或分享到其他APP。
最大的缺点是:剪同款导出时,不购买VIP就无法导出。
InShot
可以选择新建:“视频”“图片”“拼图”或看素材。总结:虽然没有开屏广告,但是有内置广告在剪辑页面的上方。
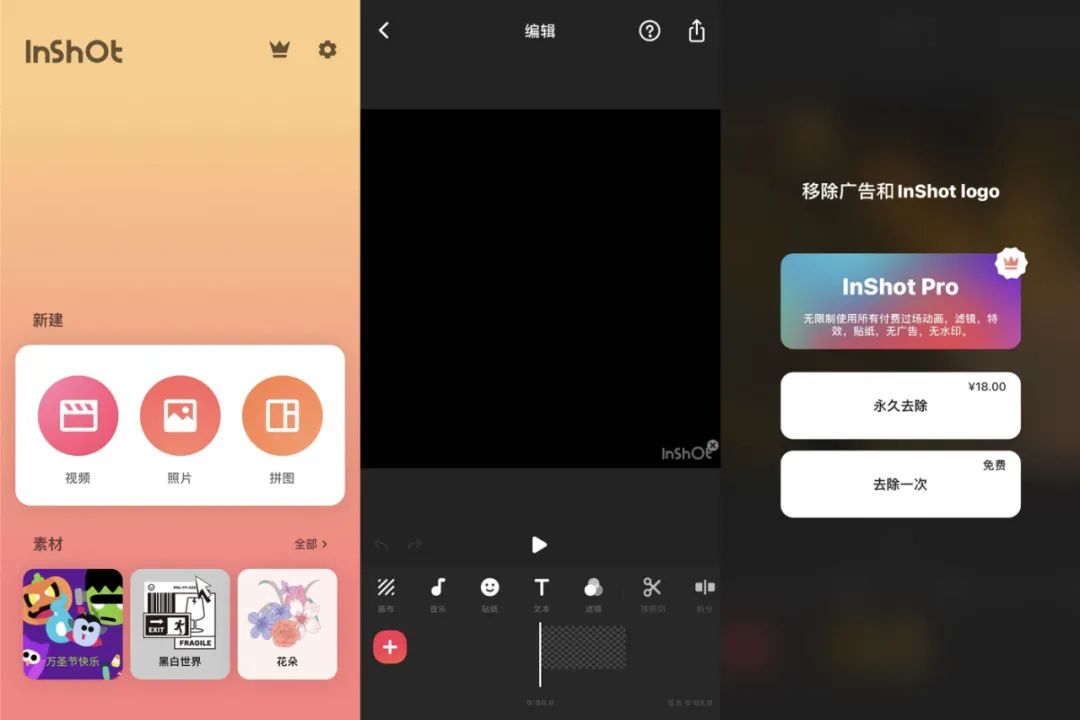
基础的编辑功能都有,比如视频剪辑、调速、转场、背景音、字幕、贴纸、滤镜、特效等等。
不过没有模板,所以更适合自己慢慢加特效或各种转场得出自己想要的结果。
购买VIP才能关掉水印,和无限制使用所有付费素材。
配音小程序:喵盐配音
喵盐配音应该是大家公认的好用的配音软件,它使用方便,无需进行下载安装,小程序搜索打开即可,不占用内存,随用随开,并且手机端与电脑端都可操作,灵活便捷,凤凰配音自带几百个配音员,包括我们日常经常听到的电影解说、广告宣传、配音旁白、可爱童声、特色方言、多国外语等等,完全可以满足用户对于声音的不同需求。
同时,它的配音技术也非常过硬,合成的声音无限接近真人发声,根本听不出是AI配音,完美做到了以假乱真,用过这款软件的小伙伴都对这一点赞不绝口,合成的语音文件可根据自身需求选择不同格式,如wav、mp3等等,可直接使用,无需进行二次转换,提高了创作效率。
