个人服务器 网站建设男女做受视频网站

由于风电、新能源汽车、机器人、工业自动化和无线充电等下游应用领域的快速发展,磁性材料行业近年来产值不断扩大,全球磁性材料市场规模在2022年突破了350亿美元,中国市场规模达800亿元人民币。特别是电子行业,无线充电技术、电感、变压器、微型电机、滤波器、扼流圈,传感器等,磁芯的应用无处不在。
一、磁芯的形状
你以为的磁芯形状是这样的:

实际上大多数是这样的:

二、变压器磁芯
以目前新能源汽车上的变压器磁芯举例:
高频变压器是变换交流电压、电流和阻抗的器件,由磁芯和线圈组成。

磁芯的形状、影响变压器的散热性、屏蔽性、造价和线圈卷绕难易度。

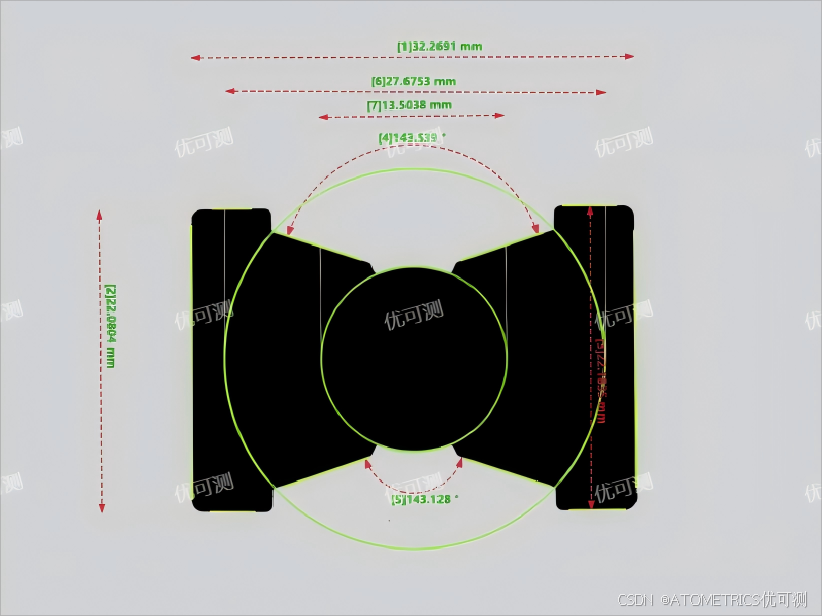
三、磁芯的几何尺寸测量解决方案
此外,磁芯的几何尺寸决定了变压器的电流大小和工作效率:
- 磁芯尺寸越大,电流越大;
- 磁芯尺寸越小,工作频率越高。
各生产厂家为确保生产的变压器符合各类电性能设计,需要对磁芯进行大量尺寸检测。
一键尺寸测量仪FM9000系列:瞬间即可完成磁芯几何尺寸测量,进行OK/NG判定,提高产品良率。
底光编程效果

表面光编程效果

2000万像素+缝隙环形光 高清晰效果
即使是多个磁芯同时测量,也可瞬间完成检测,自动判断OK/NG。
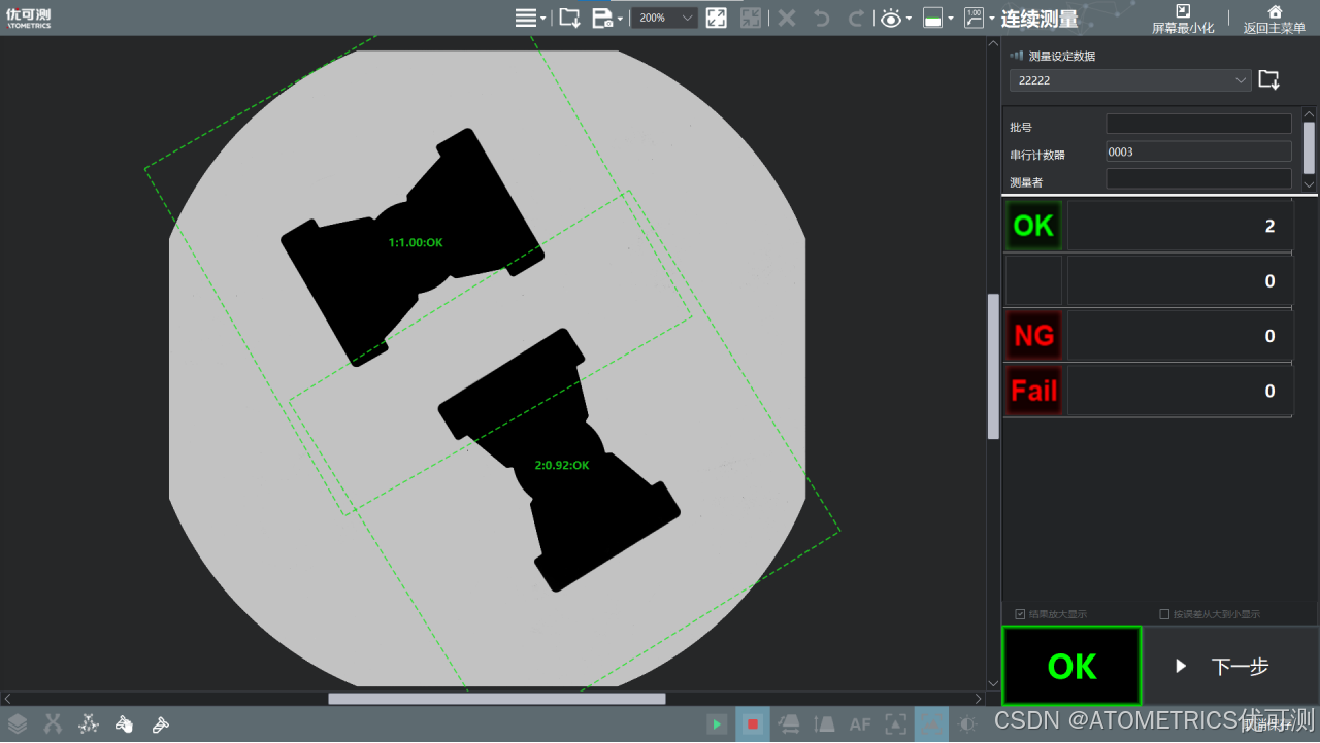
正因磁芯尺寸对产品品质影响之大,质检环节必不可少。
许多厂家面临着质检人员招工难、不同人员测量结果差异较大、测量工时漫长等问题。
一键尺寸测量仪FM-9000系列:随意放置即可瞬间精确、快速、批量测量,是解决磁芯几何尺寸测量困扰的优选方案,帮助您提升产品良率与产量!
