网站页面好了怎么做后端网站开发先前台和后台
一、AOP介绍和应用场景
Spring 中文文档 (springdoc.cn)
Spring | Home 官网
1、AOP介绍(为什么会出现AOP ?)
Java是一个面向对象(OOP)的语言,但它有一些弊端。虽然使用OOP可以通过组合或继承的方式来实现代码的重用。但当我们需要为多个不具有继承关系的对象(一般指的是两个不同的类,它们之间没有继承自同一个父类或接口。它们无法通过继承来共享属性和方法。)引入一个公共行为,例如日志、权限验证、事务等功能时,同样的代码仍然会分散到各个方法中。如果想关闭某个功能或是对其进行修改,就必须修改所有的相关方法,这样做不便于维护,而且有大量重复代码。于是AOP的出现弥补了OOP的这点不足。
AOP 是 Spring 框架提供的一个重要特性,与OOP(面向对象编程)不同的是,AOP主张将程序中相同的业务逻辑进行横向的隔离,将重复的业务逻辑抽取到一个独立的模块中,通过在运行时动态地将代码逻辑织入到目标对象的方法中,实现与业务逻辑解耦和重复代码的消除,提高了代码的可维护性和可扩展性。
2、AOP应用场景
这是官方文档中对应用场景进行的描述:

Authentication 权限 ;Caching 缓存 ; Context passing 内容传递;
Error handling 错误处理;Lazy loading 懒加载;Debugging 调试;
Logging 日志 ,tracing,profiling and monitoring 记录跟踪 优化 校准;
Performance optimization 性能优化 ;Persistence 持久化 ; Resource pooling 资源池
Synchronization 同步 ;Transactions 事务
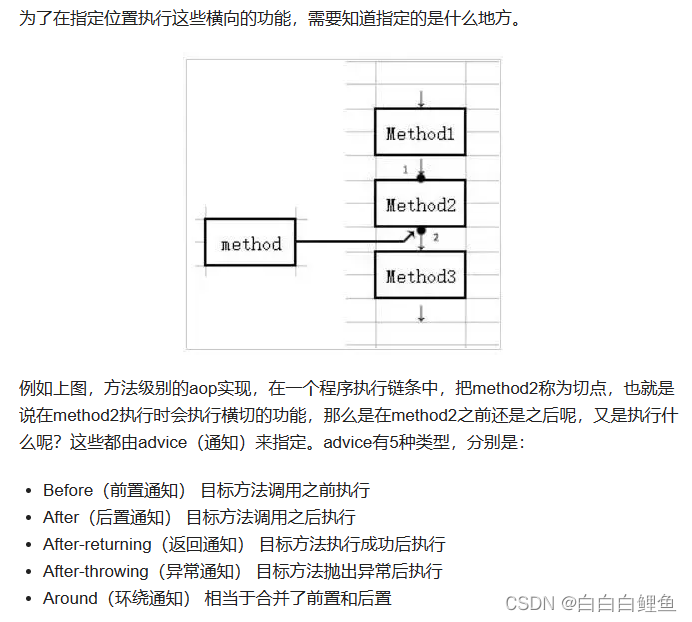
二、AOP原理
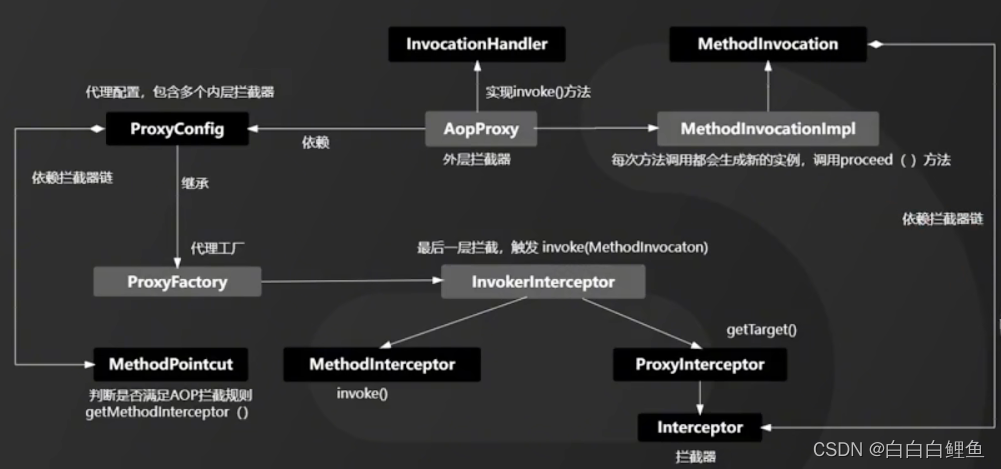
执行过程依次是

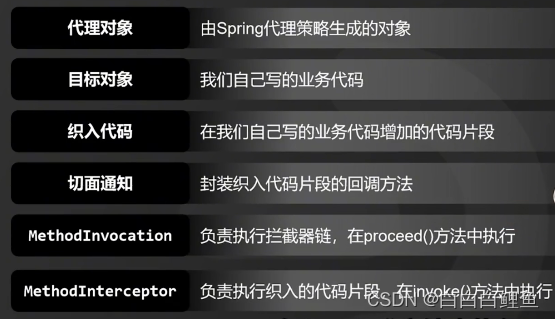

1、 在 Spring 中,创建 Bean 实例都是从 getBean()方法开始的, 在实例创建之后,Spring 容器将根据 AOP 的配置去匹配目标类的类名,看目标类的类名是否满足切面规则。如果满足满足切面规则,就会调用 ProxyFactory 创建代理 Bean 并缓存到 IoC 容器中。根据目标对象的自动选择不同的代理策略。如果目标类实现了接口,Spring 会默认选择 JDK Proxy,如果目标类没有实现接口,Spring 会默认选择 Cglib Proxy, 当然,我们也可以通过配置强制使用 Cglib Proxy
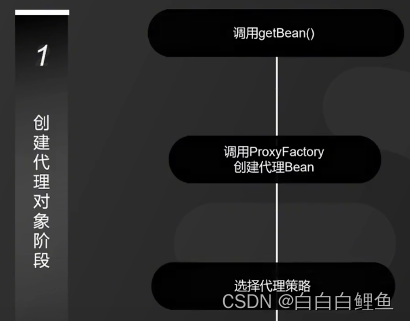
2、当用户调用目标对象的某个方法时,将会被一个叫做AopProxy 的对象拦截,Spring 将所有的调用策略封装到了这个对象中,它默认实现了 InvocationHandler 接口,也就是调用代理对象的外层拦截器。在这个接口的 invoke()方法中,会触发 MethodInvocation 的 proceed()方法。在这个方法中会按顺序执行符合所有 AOP 拦截规则的拦截器链。
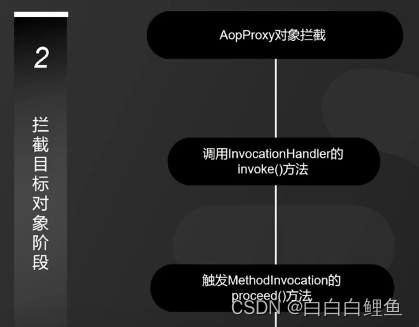
3、Spring AOP 拦截器链中的每个元素被命名为 MethodInterceptor,其实就是切面配置中的 Advice 通知。这个回调通知可以简单地理解为是新生成的代理 Bean 中的方法。也就是我们常说的被织入的代码片段,这些被织入的代码片段会在这个阶段执行。

4、MethodInterceptor 接口也有一个 invoke()方法,在 MethodInterceptor 的 invoke()方法中会触发对目标对象方法的调用,也就是反射调用目标对象的方法。

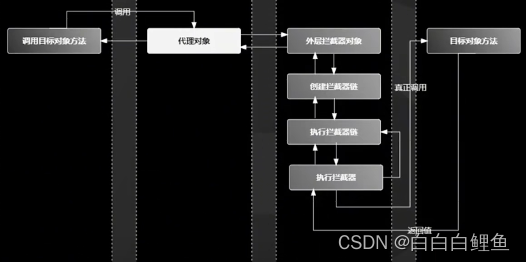
三、什么是代理模式
当谈论代理模式时,可以通过两种常见例子进行解释:买火车票和Windows里的快捷方式。
-
买火车票:假设你需要买一张火车票,但你不想亲自去火车站排队购票。那么你可以找一个代理人,让他帮你完成购票的过程。代理人负责排队、选座位、支付等操作,并最终将车票交给你。在这个例子中,代理人扮演着你与火车站之间的中介角色,你通过代理人完成了购票过程,同时也避免了亲自去火车站排队的麻烦。
-
Windows里的快捷方式:在Windows系统中,你可以使用桌面上的快捷方式来访问某个程序或文件。快捷方式实际上是一个代理,它引用了目标程序或文件的位置信息,并提供了一个方便的入口,使得你可以通过点击快捷方式来快速访问目标内容。快捷方式隐藏了底层的具体实现细节,简化了用户的操作过程。
下面是买火车票的示例代码:
// 创建一个抽象主题接口
interface Ticket {void purchase();
}// 创建真实主题类,即需要购买火车票的对象
class TrainTicket implements Ticket {public void purchase() {System.out.println("购买火车票");}
}// 创建代理类,即代理对象
class TicketProxy implements Ticket {private TrainTicket ticket;public void purchase() {if (ticket == null) {ticket = new TrainTicket();}// 通过代理对象调用真实对象的方法prePurchase();ticket.purchase();postPurchase();}private void prePurchase() {System.out.println("代理人处理排队、选座位等操作");}private void postPurchase() {System.out.println("代理人将车票交给顾客");}
}// 客户端代码
public class ProxyPatternExample {public static void main(String[] args) {// 创建代理对象,并通过它来购买火车票Ticket ticketProxy = new TicketProxy();ticketProxy.purchase();}
} 在上述示例中,Ticket是一个抽象主题接口定义了购票的方法。TrainTicket是真实主题类,代表了真正需要购票的对象。TicketProxy是代理类,实现了Ticket接口,它维护了一个对TrainTicket对象的引用,并在调用purchase方法前后进行了一些额外的操作,如排队和交票。通过创建代理对象并调用其purchase方法,我们可以间接地让代理对象完成购票过程,并在其中添加一些特定功能,而无需直接访问真实主题对象。
而代理模式又分为两种,动态代理和静态代理。它们都是面向对象中的代理模式,作用都是为了在客户端与目标对象之间起到一个中介作用,拦截对目标对象的访问,以达到增强目标对象的功能或控制其访问权限的目的。
两者的区别如下:
静态代理是在编译时期就已经确定的代理关系,代理类和目标类都是在编译时期就已经存在的。在静态代理中,需要手动创建代理类,代理类和目标类之间的关系是固定的。每当需要代理一个新的接口或者类时,都需要手动编写一个新的代理类。
而动态代理是在运行时动态生成的代理类。通过 Java 提供的 java.lang.reflect.Proxy 类和 java.lang.reflect.InvocationHandler 接口,可以在运行时动态生成代理对象。动态代理不需要手动编写代理类,它在运行时根据接口信息动态地生成代理对象。使用动态代理时,代理类和目标类之间的关系是灵活的。只需要定义一个普通的接口,通过 InvocationHandler 来处理方法调用,可以代理多个不同的接口或类。
动态代理的优点在于可以减少代码量,避免了编写大量重复的代理类。同时,它还可以实现更灵活的代理逻辑,可以在运行时动态地修改代理行为。
总的来说,动态代理和静态代理都是代理模式的实现方式,静态代理通过手动编写代理类实现,而动态代理则通过反射机制在运行时动态生成代理类。
四、Spring AOP 的代理机制
Spring 在运行期会为目标对象生成一个动态代理对象,并在代理对象中实现对目标对象的增强。Spring AOP 的底层是通过以下 2 种动态代理机制,为目标对象(Target Bean)执行横向织入的。

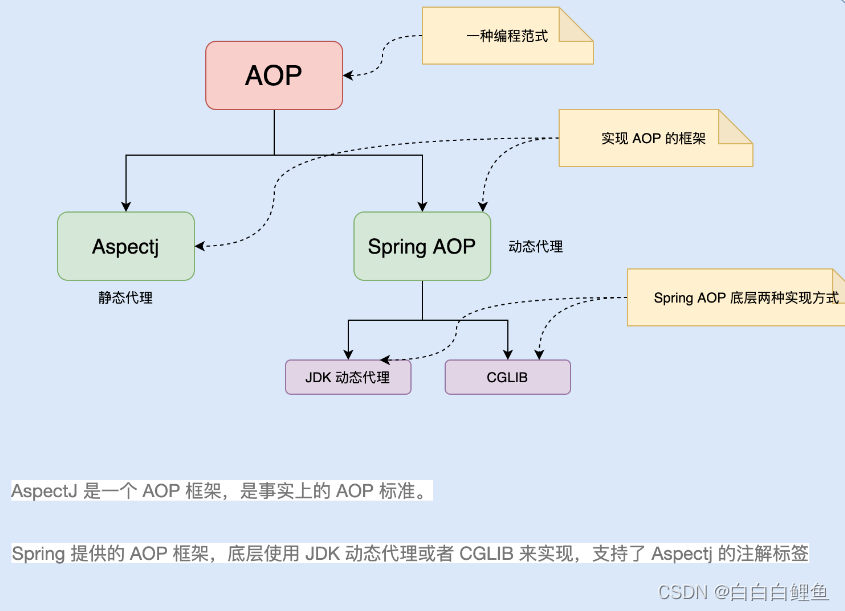
在 Spring AOP 的配置中,可以通过 XML 或注解的方式声明切入点和切面。XML 方式需要配置切入点表达式、通知类型(如前置通知、后置通知等)和切面类的引用;注解方式则通过在切面类上添加注解来指定切入点和通知类型。
Spring默认使用JDK动态代理,在需要代理类而不是代理接口的时候,Spring会自动切换为使用CGLIB代理,不过现在的项目都是面向接口编程,所以JDK动态代理相对来说用的还是多一些。
JDK代理和CGLIB代理有什么区别?
都不需要创建代理类,JDK 在运行时为我们动态的来创建,JDK代理是接口 。若目标类不存在接口,则使用Cglib生成代理,不管是JDK代理还是Cglib代理本质上都是对字节码进行操作。
| 代理技术 | 描述 |
|---|---|
| JDK 动态代理 | Spring AOP 默认的动态代理方式,若目标对象实现了若干接口,Spring 使用 JDK 的 java.lang.reflect.Proxy 类进行代理。 |
| CGLIB 动态代理 | 若目标对象没有实现任何接口,Spring 则使用 CGLIB 库生成目标对象的子类,以实现对目标对象的代理。 |
注意:由于被标记为 final 的方法是无法进行覆盖的,因此这类方法不管是通过 JDK 动态代理机制还是 CGLIB 动态代理机制都是无法完成代理的。
面试:让你实现一个JDK实现动态代理?你的思路是什么?

import java.lang.reflect.InvocationHandler;
import java.lang.reflect.Method;
import java.lang.reflect.Proxy;// 定义接口
interface Hello {void sayHello();
}// 实现 InvocationHandler 接口
class MyInvocationHandler implements InvocationHandler {private Object target;public MyInvocationHandler(Object target) {this.target = target;}@Overridepublic Object invoke(Object proxy, Method method, Object[] args) throws Throwable {// 在方法调用前后添加自定义逻辑System.out.println("Before method invocation");Object result = method.invoke(target, args);System.out.println("After method invocation");return result;}
}public class DynamicProxyExample {public static void main(String[] args) {// 创建被代理对象Hello hello = new HelloImpl();// 创建 InvocationHandler 实例MyInvocationHandler handler = new MyInvocationHandler(hello);// 创建代理对象Hello proxyHello = (Hello) Proxy.newProxyInstance(hello.getClass().getClassLoader(),hello.getClass().getInterfaces(),handler);// 调用代理对象的方法proxyHello.sayHello();}
}// 实现接口
class HelloImpl implements Hello {@Overridepublic void sayHello() {System.out.println("Hello World!");}
}如果使用CGLIB来实现动态代理要怎么实现呢 ?
引入 CGLIB 的依赖。在 Maven 项目中,可以添加以下依赖项到 pom.xml 文件中:
<dependency><groupId>cglib</groupId><artifactId>cglib</artifactId><version>3.3.0</version>
</dependency>
创建一个普通的类作为目标类,该类不需要实现任何接口。例如:
public class TargetClass {public void doSomething() {System.out.println("Doing something...");}
}
创建一个实现了 MethodInterceptor 接口的类,该类负责处理方法的调用。在 intercept 方法中,可以编写逻辑来处理代理对象的操作。例如:
import net.sf.cglib.proxy.MethodInterceptor;
import net.sf.cglib.proxy.MethodProxy;import java.lang.reflect.Method;public class MyMethodInterceptor implements MethodInterceptor {@Overridepublic Object intercept(Object obj, Method method, Object[] args, MethodProxy proxy) throws Throwable {System.out.println("Before method invocation");Object result = proxy.invokeSuper(obj, args);System.out.println("After method invocation");return result;}
}
使用 CGLIB 创建代理对象。通过调用 Enhancer.create 方法,传入目标类的 Class 对象和 MethodInterceptor 对象,创建代理对象。例如:
import net.sf.cglib.proxy.Enhancer;public class CglibDynamicProxyExample {public static void main(String[] args) {// 创建目标类的实例TargetClass target = new TargetClass();// 创建 MethodInterceptor 实例MyMethodInterceptor interceptor = new MyMethodInterceptor();// 使用 Enhancer 创建代理对象TargetClass proxy = (TargetClass) Enhancer.create(target.getClass(),interceptor);// 调用代理对象的方法proxy.doSomething();}
}
运行上述代码,会输出以下结果:
Before method invocation
Doing something...
After method invocationCGLIB 可以在运行时生成目标类的子类,并通过拦截器拦截目标方法的调用。这样可以实现对目标方法的增强或拦截操作
五、实例—实现AOP对日志的记录
步骤:
先要引入aop依赖
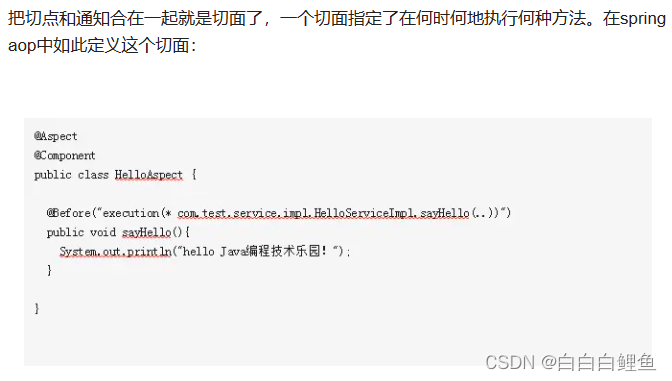
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId></dependency>然以根据以下三个步骤




import com.fasterxml.jackson.databind.ObjectMapper;
import org.apache.commons.lang3.builder.ToStringBuilder;
import org.aspectj.lang.JoinPoint;
import org.aspectj.lang.ProceedingJoinPoint;
import org.aspectj.lang.annotation.*;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
import org.springframework.stereotype.Component;
import org.springframework.web.context.request.RequestContextHolder;
import org.springframework.web.context.request.ServletRequestAttributes;import javax.servlet.http.HttpServletRequest;
import java.util.Arrays;/*** 使用@Before在切入点开始处切入内容* 使用@After在切入点结尾处切入内容* 使用@AfterReturning在切入点return内容之后切入内容(可以用来对处理返回值做一些加工处理)* 使用@Around在切入点前后切入内容,并自己控制何时执行切入点自身的内容* 使用@AfterThrowing用来处理当切入内容部分抛出异常之后的处理逻辑*/@Aspect /**Description: 使之成为切面类*/
@Component /**Description: 把切面类加入到IOC容器中*/
public class AopLog {private Logger logger = LoggerFactory.getLogger(this.getClass());//线程局部的变量,解决多线程中相同变量的访问冲突问题。ThreadLocal<Long> startTime = new ThreadLocal<>();//定义切点 1@Pointcut("execution(public * com.example..*.*(..))")public void aopWebLog() {}//定义切点 2@Pointcut("execution(public * com.example..*.*(..))")public void myPointcut() {}@Before("aopWebLog()")public void doBefore(JoinPoint joinPoint) throws Throwable {startTime.set(System.currentTimeMillis());// 接收到请求,记录请求内容ServletRequestAttributes attributes = (ServletRequestAttributes) RequestContextHolder.getRequestAttributes();HttpServletRequest request = attributes.getRequest();// 记录下请求内容logger.info("URL : " + request.getRequestURL().toString());logger.info("HTTP方法 : " + request.getMethod());logger.info("IP地址 : " + request.getRemoteAddr());logger.info("类的方法 : " + joinPoint.getSignature().getDeclaringTypeName() + "." + joinPoint.getSignature().getName());//logger.info("参数 : " + Arrays.toString(joinPoint.getArgs()));logger.info("参数 : " + request.getQueryString());}@AfterReturning(pointcut = "aopWebLog()",returning = "retObject")public void doAfterReturning(Object retObject) throws Throwable {// 处理完请求,返回内容logger.info("应答值 : " + retObject);logger.info("费时: " + (System.currentTimeMillis() - startTime.get()));}//抛出异常后通知(After throwing advice) : 在方法抛出异常退出时执行的通知。@AfterThrowing(pointcut = "aopWebLog()", throwing = "ex")public void addAfterThrowingLogger(JoinPoint joinPoint, Exception ex) {logger.error("执行 " + " 异常", ex);}@Around("myPointcut()")public Object mylogger (ProceedingJoinPoint pjp) throws Throwable {String className = pjp.getTarget().getClass().toString();String methodName = pjp.getSignature().getName();Object[] arry = pjp.getArgs();ObjectMapper mapper = new ObjectMapper();logger.info("调用前:"+className+":"+methodName+"传递的参数为:"+mapper.writeValueAsString(arry));Object obj = pjp.proceed();logger.info("调用后"+className+":"+methodName+"返回值为:"+mapper.writeValueAsString(obj));return obj;}}@RestController
public class AopLogController {
// @GetMapping("/aoptest")
// public String aVoid(){
// return "hello aop test";
// }@GetMapping("/hello")public String hello (@RequestParam("name")String name,@RequestParam("age")String age){return "hello"+name+"age"+age;}
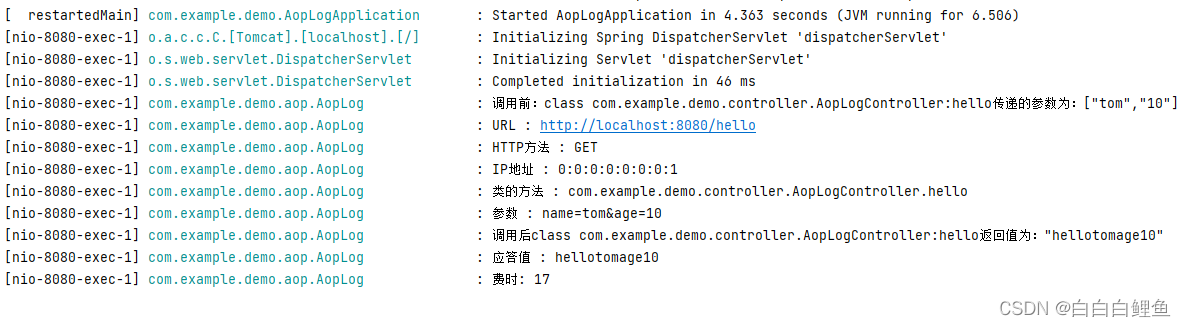
}运行:
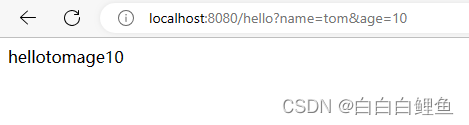
可以看到日志已经打印出来了。