建设网站注意青岛工程建设监理公司网站
现在很多的宣传片会通过扫码的方式来展示,通过将视频生成二维码之后,其他人就可以扫码来查看视频内容,从而简化获取视频的过程,提升视频传播的效率及用户查看视频的便捷性。目前,日常生活和工作中就有视频二维码的应用,用这种方式来分享视频,那么视频二维码制作的步骤是什么样的呢?
想要将视频转二维码图片,那么比较简单的一种方法可以通过在线的二维码生成器工具来制作,只需要通过几步简单的操作,就可以将多种格式的视频生成二维码,下面分享一下具体的制作方法。
在网上找到机智熊二维码生成器工具后选择【音视频】功能,点击页面上传按钮添加本地的视频文件。

视频上传后程序自动做转码处理,成功上传后可以添加视频封面、设置默认全屏、允许下载、竖屏播放等功能。
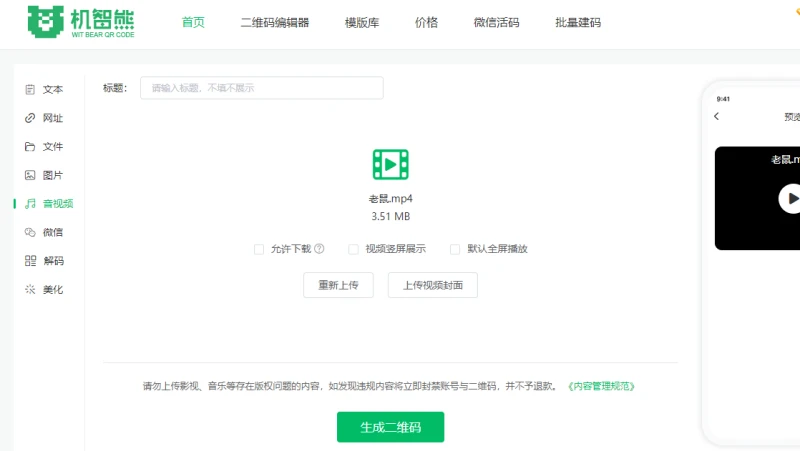
点击生成二维码按钮,自动将视频转换成二维码图片,扫码即可播放视频。
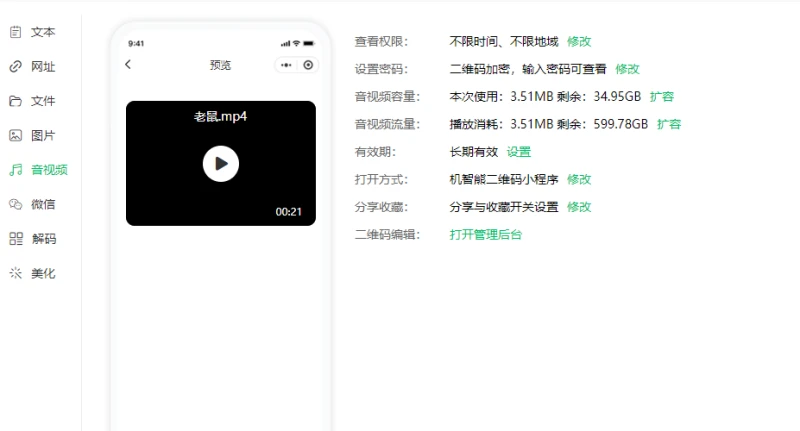
以上方法可以轻松将视频做成二维码,只需简单几步操作就能够实现视频播放二维码的展示效果,有需要的小伙伴可以将自己的视频按步骤来生成二维码,希望以上内容对大家有所帮助。
