德国网站的后缀名美食网站设计的代码
【Vue中给输入框加入js验证_blur失去焦点进行校验】
通俗一点就是给输入框加个光标离开当前文本输入框时,然后对当前文本框内容进行校验判断
具体如下:
1.先给文本框加属性 @blur=“validatePhoneNumber”
<el-input v-model=“entity.telephone” @blur=“validatePhoneNumber” :disabled=“disabled”>
{{ errorText }}
2.在data中对需要值进行默认赋值,或者称之为自定义
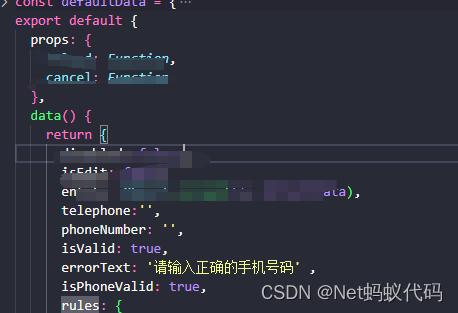
telephone:‘’,
phoneNumber: ‘’,
isValid: true,
errorText: ‘请输入正确的手机号码’ ,
isPhoneValid: true,
3.在method中自定义校验的方法
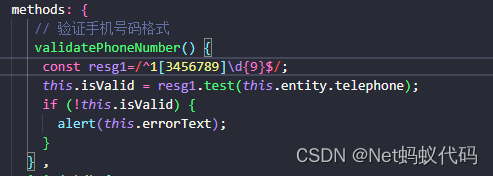
validatePhoneNumber() { const resg1=/^1[3456789]\d{9}$/;this.isValid = resg1.test(this.entity.telephone); if (!this.isValid) { alert(this.errorText); }
}
