我网站正在建设中做网站是不是太麻烦了
开始使用富文本组件editor时,不知如何调用相关API设置富文本内容和获取内容,本文将举例详解
目录
一.了解editor组件的常用属性及相关API
1.属性常用说明
2.富文本相关API说明
1)editorContext
2) editorContext.setContents(OBJECT)
3)editorContext.getContents(OBJECT)
二. 使用@ready属性,设置富文本初始内容为后端接口内容
1.onLoad获取后端接口数据
注意:这里设置了一个标示isDataLoaded(默认为false) ,用来确保先获得后端的数据
2.@ready="onEditorReady",编写onEditorReady方法,富文本初始加载数据
3.@input="onEditorInput",编写onEditorInput方法,富文本内容改变时触发
一.了解editor组件的常用属性及相关API
<editorid="editor"placeholder="开始输入..."showImgSizeshowImgToolbarshowImgResize@ready="onEditorReady"@input="onEditorInput"
></editor>1.属性常用说明
| 属性 | 类型 | 默认值 | 必填 | 说明 |
|---|---|---|---|---|
| placeholder | string | 否 | 提示信息 | |
| show-img-size | boolean | false | 否 | 点击图片时显示图片大小控件 |
| show-img-toolbar | boolean | false | 否 | 点击图片时显示工具栏控件 |
| show-img-resize | boolean | false | 否 | 点击图片时显示修改尺寸控件 |
| @ready | eventhandle | 否 | 编辑器初始化完成时触发 | |
| @input | eventhandle | 否 | 编辑器内容改变时触发,detail = {html, text, delta} |
2.富文本相关API说明
1)editorContext
editor 组件对应的 editorContext 实例,可通过 uni.createSelectorQuery 获取。
onEditorReady() {uni.createSelectorQuery().select('#editor').context((res) => {this.editorCtx = res.context}).exec()}
2) editorContext.setContents(OBJECT)
初始化编辑器内容,html和delta同时存在时仅delta生效
OBJECT 参数说明
| 属性 | 类型 | 默认值 | 必填 | 说明 |
|---|---|---|---|---|
| html | String | 否 | 带标签的HTML内容 | |
| delta | Object | 否 | 表示内容的delta对象 | |
| success | Function | 否 | 接口调用成功的回调函数 | |
| fail | Function | 否 | 接口调用失败的回调函数 | |
| complete | Function | 否 | 接口调用结束的回调函数(调用成功、失败都会执行) |
3)editorContext.getContents(OBJECT)
获取编辑器内容
OBJECT 参数说明
| 属性 | 类型 | 默认值 | 必填 | 说明 |
|---|---|---|---|---|
| success | Function | 否 | 接口调用成功的回调函数 | |
| fail | Function | 否 | 接口调用失败的回调函数 | |
| complete | Function | 否 | 接口调用结束的回调函数(调用成功、失败都会执行) |
object.success 回调函数
| 属性 | 类型 | 说明 |
|---|---|---|
| html | string | 带标签的 HTML 内容 |
| text | string | 纯文本内容 |
| delta | Object | 表示内容的 delta 对象 |
二. 使用@ready属性,设置富文本初始内容为后端接口内容
1.onLoad获取后端接口数据


注意:这里设置了一个标示isDataLoaded(默认为false) ,用来确保先获得后端的数据
2.@ready="onEditorReady",编写onEditorReady方法,富文本初始加载数据

说明:①调用初始化方法,目的是创建editor组件对应的 editorContext (实例上下文)
②调用设置富文本内容的方法
③若获取了后端的数据,调用setContents设置富文本内容
④若没有获取到,则使用定时器,0.001s后重试
测试:启动后端和前端,前端运行界面如下---->

3.@input="onEditorInput",编写onEditorInput方法,富文本内容改变时触发
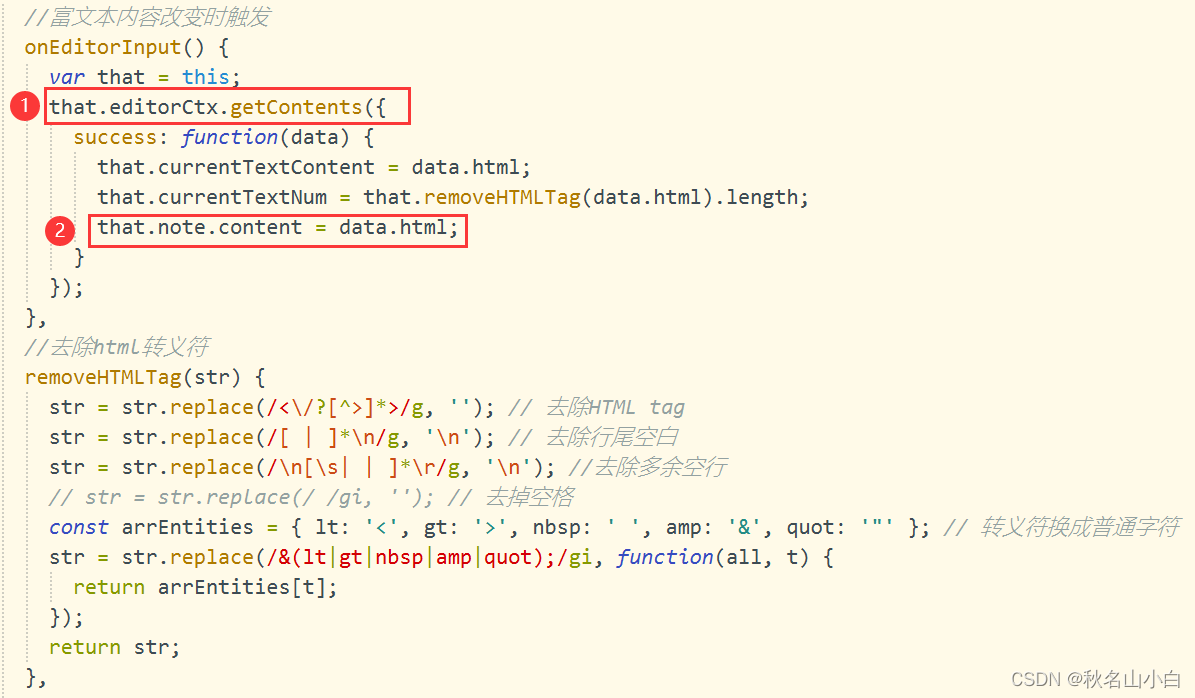
说明:① 调用获取富文本内容方法getContents
②在回调函数中,设置后端内容=富文本的内容