百度上面做企业网站怎么做广州新闻头条最新消息
简介
为了验证用户登录情况以及减轻服务器的压力,减少频繁的查询数据库,使服务器更加健壮。有些登录不是用 cookie 来验证的,是用 token 参数来判断是否登录。token 传参有两种一种是放在请求头里,本质上是跟 cookie 是一样的,只
是换个单词而已;另外一种是在 url 请求参数里,这种更直观。
b站最牛Jmeter接口测试和Jmeter接口自动化测试全集![]() https://www.bilibili.com/video/BV1hq4y1K75i/?spm_id_from=333.999.0.0
https://www.bilibili.com/video/BV1hq4y1K75i/?spm_id_from=333.999.0.0
登录返回token
1、如下图的这个登录接口,就是没有 cookies的登录接口。
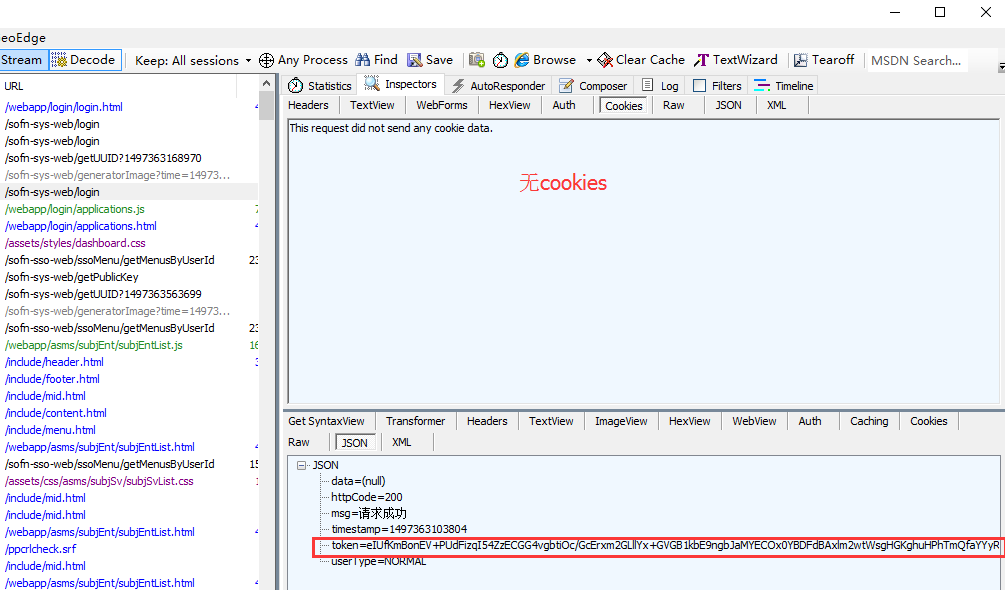
2、但是这个登录接口,登录成功后有返回token,如下图
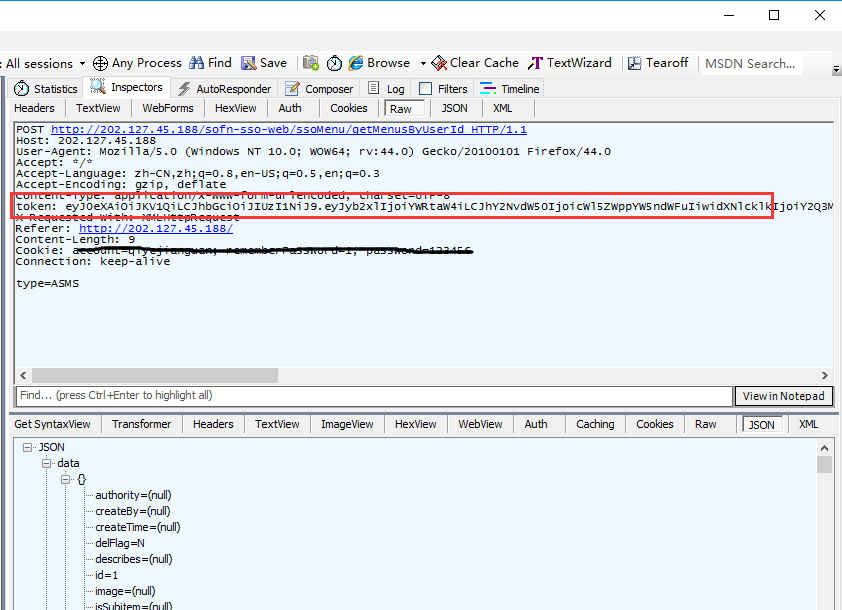
请求头带token
1、登录成功后继续操作其它页面,发现post请求的请求头,都会带有token参数
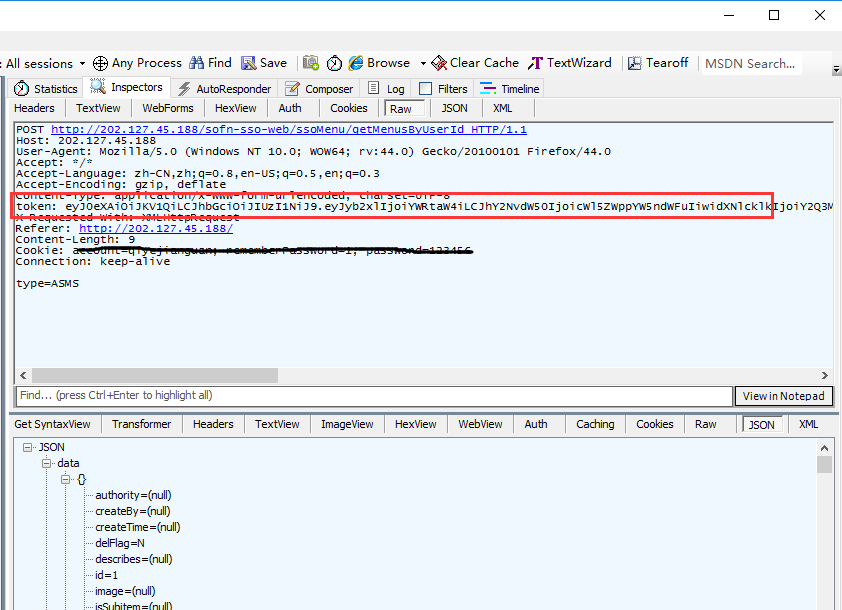
2、这种请求其实比cookie更简单,直接把登录后的token放到头部即可
token关联
1、用脚本实现登录,获取token参数,获取后传参到请求头就可以了
2、如果登录有验证码,前面的脚本登录步骤就省略了,自己手动登录后获取token
参考代码
1 # coding:utf-82 import requests3 header = { # 登录抓包获取的头部4 "User-Agent": "Mozilla/5.0 (Windows NT 10.0; WOW64; rv:44.0) Gecko/20100101 Firefox/44.0",5 "Accept": "*/*",6 "Accept-Language": "zh-CN,zh;q=0.8,en-US;q=0.5,en;q=0.3",7 "Accept-Encoding": "gzip, deflate",8 "Content-Type": "application/x-www-form-urlencoded; charset=UTF-8",9 "X-Requested-With": "XMLHttpRequest",
10 "Content-Length": "423",
11 "Connection": "keep-alive"
12 }
13 body = {"key1": "value1",
14 "key2": "value2"} # 这里账号密码就是抓包的数据
15 s = requests.session()
16 login_url = "http://xxx.login" # 自己找带token网址
17 login_ret = s.post(login_url, headers=header, data=body)
18 # 这里token在返回的json里,可以直接提取
19 token = login_ret.json()["token"]
20 # 这是登录后发的一个post请求
21 post_url = "http://xxx"
22 # 添加token到请求头
23 header["token"] = token
24 # 如果这个post请求的头部其它参数变了,也可以直接更新
25 header["Content-Length"]="9"
26 body1 = {
27 "key": "value"
28 }
29 post_ret = s.post(post_url, headers=header, data=body1)
30 print post_ret.content
小结
Token的意义及用法
一.Token的来源:
当客户端多次向服务端请求数据时,服务端就需要多次从数据库中查询用户名和密码并进行对比,判断用户名和密码是否正确,并作出相应提示。但这样无疑会增加服务器端的运行压力,是否可以有一种方式只需要验证用户就是之前的用
户而不需要每次在客户端请求数据时都需要查询数据库判断用户名和密码是否正确。在这种请求下,引入了token来解决服务器端多次访问数据库问题。
1、什么是Token:
Token是服务端端生成的一串字符串,作为客户端进行请求时辨别客户身份的的一个令牌。当用户第一次登录后,服务器生成一个Token便将此Token返回给客户端,以后客户端只需带上这个Token前来请求数据即可,无需再次带上用户名和密码。
2、使用Token的目的:
Token的目的是为了验证用户登录情况以及减轻服务器的压力,减少频繁的查询数据库,使服务器更加健壮。
二. Token的运用流程:
1、当用户首次登录成功之后, 服务器端就会生成一个 token 值,这个值,会在服务器保存token值(保存在数据库中),再将这个token值返回给客户端;
2、客户端拿到 token 值之后,进行保存 (保存位置由服务器端设置);
3、以后客户端再次发送网络请求(一般不是登录请求)的时候,就会将这个 token 值附带到参数中发送给服务器.;
4、服务器接收到客户端的请求之后,会取出token值与保存在本地(数据库)中的token值进行比较;
5、如果两个 token 值相同, 说明用户登录成功过!当前用户处于登录状态;
6、如果没有这个 token 值, 没有登录成功;
7、如果 token 值不同: 说明原来的登录信息已经失效,让用户重新登录;
8、Django Rest framework中JWT的使用稍有差异,这里不做详细说明。
总结:现阶段如何突出重围呢?唯有不断的学习,下面是软件测试到测试开发全职业生涯全套学习资料
【需要的可以点击下方官方推广小卡片扫码备注000免费领取】

