长城集团建设有限公司网站成都公司网页制作电话
第一章:继承的概念及定义
1.1继承的概念
继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类,称派生类。继承呈现了面向对象程序设计的层次结构,体现了由简单到复杂的认知过程。以前我们接触的复用都是函数复用,继承是类设计层次的复用。
#include <iostream>
using namespace std;class Person {
public:void Print() {cout << "name:" << _name << endl;cout << "age:" << _age << endl;}
protected:string _name = "peter";//姓名int _age = 18;//年龄
};//继承后父类的Person的成员(成员函数+成员变量)都会变成子类的一部分。
//这里体现出了Student和Teacher复用了Person的成员。
class Student : public Person {
protected:int _stuid;//学号
};class Teacher : public Person {
protected:int _jobid;//工号
};int main() {Student s;Teacher t;//使用监视窗口查看Student和Teacher对象,可以看到变量的复用。s.Print();t.Print();//调用Print可以看到成员函数的复用。return 0;
}1.2 继承定义
1.2.1定义格式

1.2.2继承关系和访问限定符

1.2.3继承基类成员访问方式的变化
| 类成员/继承方式 | public继承 | protected继承 | private继承 |
| 基类的public成员 | 派生类的public成员 | 派生类的protected成员 | 派生类的private成员 |
| 基类的protected成员 | 派生类的protected成员 | 派生类的protected成员 | 派生类的private成员 |
| 基类的private成员 | 在派生类中不可见 | 在派生类中不可见 | 在派生类中不可见 |
总结:
- 基类private成员在派生类中无论以什么方式继承都是不可见的。这里的不可见是指基类的私有成员还是被继承到了派生类对象中,但是语法上限制派生类对象不管在类里面还是类外面都不能去访问它。
- 基类private成员在派生类中是不能被访问,如果基类成员不想在类外直接被访问,但需要在派生类中能访问,就定义为protected。可以看出保护成员限定符是因继承才出现的。
- 实际上面的表格我们进行一下总结会发现,基类的私有成员在子类都是不可见。基类的其他成员在子类的访问方式 == Min(成员在基类的访问限定符,继承方式),public > protected > private。
- 使用关键字class时默认的继承方式是private,使用struct时默认的继承方式是public,不过最好显示的写出继承方式。
- 在实际运用中一般使用都是public继承,几乎很少使用protetced/private继承,也不提倡使用protetced/private继承,因为protetced/private继承下来的成员都只能在派生类的类里面使用,实际中扩展维护性不强。
第二章:基类和派生类对象赋值转换
- 派生类对象可以赋值给基类的对象 / 基类的指针 / 基类的引用。这里有个形象的说法叫切片或者切割。寓意把派生类中父类那部分切来赋值过去。
- 基类对象不能赋值给派生类对象。
- 基类的指针或者引用可以通过强制类型转换赋值给派生类的指针或者引用。但是必须是基类的指针是指向派生类对象时才是安全的。这里基类如果是多态类型,可以使用RTTI(Run-Time Type Information)的dynamic_cast 来进行识别后进行安全转换。(ps:这个我们后面再讲解,这里先了解一下)
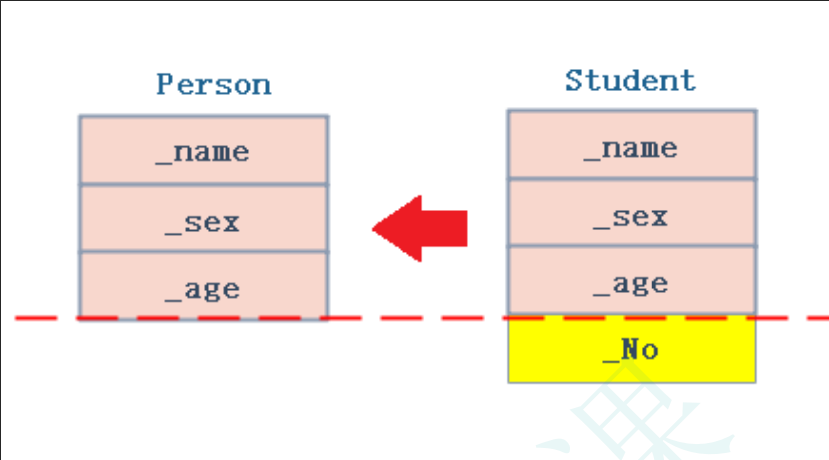
//1.子类对象可以赋值给父类对象/指针/引用
//2.基类对象不能赋值给派生类对象
class Person {
protected:string _name;string _sex;int _age;
};class Student : public Person {
public:int _No;
};int main() {double d = 2.2;//int& i = d;//编译报错const int& i = d;string str = "xxxx";//string& rstr = "xxxx";//编译报错const string& rstr = "xxxx";//隐式类型转换会生成临时对象,临时对象具有常性,所以引用加constStudent s;Person p = s;//公有继承情况下,子类(派生类)可以赋值给父类(基类)Person& rp = s;//public继承,子类对父类是is-a的关系。//子类对象赋值给父类对象/父类指针/父类的引用可以认为是天然的,中间不产生临时对象,这个叫父子类赋值兼容规则(切割/切片)。//子类对象赋值给父类对象:把子类中 父类也有的成员 赋值给父类//父类引用子类:仅引用子类中 父类也有的成员return 0;
}第三章:继承中的作用域
- 在继承体系中基类和派生类都有独立的作用域。
- 子类和父类中有同名成员,子类成员将屏蔽父类对同名成员的直接访问,这种情况叫隐藏,也叫重定义。(在子类成员函数中,可以使用 基类::基类成员 显示访问)
- 需要注意的是如果是成员函数的隐藏,只需要函数名相同就构成隐藏。
- 注意在实际中在继承体系里面最好不要定义同名的成员。
class Person {
protected:string _name = "小李子";int _num = 111;//身份证号
};class Student : public Person {
public:void Print() {cout << "姓名:" << _name << endl;cout << "身份证号:" << Person::_num << endl;cout << "学号:" << _num << endl;//这里访问的是子类Student的_num}
protected:int _num = 999;//学号//父类中有_num,子类中也能有_num。他们是两个独立的作用域//Student的_num和Person的_num构成隐藏关系,可以看出这样代码虽然能跑,但是非常容易混淆
};
//1.在继承体系中基类和派生类都有独立的作用域。
//2.子类和父类中有同名成员,子类成员将屏蔽父类对同名成员的直接访问,这种情况叫隐藏,
// 也叫重定义。(在子类成员函数中,可以使用 基类::基类成员 显示访问)
void Test1() {Student s1;s1.Print();
};//B中的fun和A中的fun不是构成重载,因为不是在同一作用域
//B中的fun和A中的fun构成隐藏,成员函数满足函数名相同就构成隐藏。
class A {
public:void fun() {cout << "func()" << endl;}
};class B : public A {
public:void fun(int i) {A::fun();cout << "func(int i)->" << i << endl;}
};void Test2() {B b;b.fun(10);//b.fun();//不能调用父类,因为被子类隐藏了b.A::fun();//指定父类作用域才能调用
};
//3.需要注意的是如果是成员函数的隐藏,只需要函数名相同就构成隐藏。
//4.注意在实际中在继承体系里面最好不要定义同名的成员。第四章:派生类的默认成员函数
6个默认成员函数,“默认”的意思就是指我们不写,编译器会变我们自动生成一个,那么在派生类中,这几个成员函数是如何生成的呢?
- 派生类的构造函数必须调用基类的构造函数初始化基类的那一部分成员。如果基类没有默认的构造函数,则必须在派生类构造函数的初始化列表阶段显示调用。
- 派生类的拷贝构造函数必须调用基类的拷贝构造完成基类的拷贝初始化。
- 派生类的operator=必须要调用基类的operator=完成基类的复制。
- 派生类的析构函数会在被调用完成后自动调用基类的析构函数清理基类成员。因为这样才能保证派生类对象先清理派生类成员再清理基类成员的顺序。
- 派生类对象初始化先调用基类构造再调派生类构造。
- 派生类对象析构清理先调用派生类析构再调基类的析构。
- 因为后续一些场景析构函数需要构成重写,重写的条件之一是函数名相同(这个我们后面会讲解)。那么编译器会对析构函数名进行特殊处理,处理成destrutor(),所以父类析构函数不加virtual的情况下,子类析构函数和父类析构函数构成隐藏关系。
#include <iostream>
using namespace std;class Person {
public:Person(const char* name = "peter"): _name(name) {cout << "Person()" << endl;}Person(const Person& p): _name(p._name) {cout << "Person(const Person& p)" << endl;}Person& operator=(const Person& p) {cout << "Person operator=(const Person& p)" << endl;if (this != &p)_name = p._name;return *this;}~Person() { cout << "~Person()" << endl; }
protected:string _name;//姓名
};class Student : public Person {
public://构造函数//如果子类[没有]显式定义构造函数,会自动调用父类的默认构造函数//如果子类显示定义构造函数,要把父类当成一个完整对象去初始化Student(const char* name, int num)//:_name(name) 该方式错误: Person(name) //用一个像匿名对象的方式调用父类构造函数, _num(num) {cout << "Student()" << endl;}//1.父类[没有]默认构造函数 → 必须显式调用父类的某个构造函数。//2.父类有默认构造函数 → 可以不显式调用(编译器自动调用),但如果你想用特定值初始化父类成员,仍然需要显式调用。//3.调用方式:在子类构造函数的初始化列表中,像“匿名对象”一样调用父类构造函数//拷贝构造//如果子类[没有]显式定义拷贝构造函数,会自动调用父类的拷贝构造函数Student(const Student& s): Person(s)//子类赋值给父类的引用,触发切片。只赋值了子类中父类有的那部分, _num(s._num) {cout << "Student(const Student& s)" << endl;}//1.如果父类有默认拷贝构造函数(即没有显式定义,且所有成员都可拷贝),//子类可以不显式调用父类拷贝构造,编译器会自动调用父类的默认拷贝构造。//2.如果父类没有默认拷贝构造函数(例如,父类显式定义了拷贝构造但未提供默认版本,或者某些成员不可拷贝),//子类必须在初始化列表中显式调用父类的拷贝构造函数,否则编译错误//赋值重载//如果子类[没有]显式定义赋值重载,会自动调用父类的赋值重载Student& operator=(const Student& s) {cout << "Student& operator= (const Student& s)" << endl;if (this != &s) {//operator=(s);//错误,栈溢出。父类和子类的赋值构成隐藏,这种方式是调用子类的赋值重载Person::operator=(s);_num = s._num;}return *this;}//由于多态的原因,析构函数会被统一处理成destructor//子类和父类的析构构成隐藏~Student() {//~Person();//错误,构成隐藏,所以这种方式是访问子类的析构//Person::~Person();//显示调用的方式。而main函数中只有3个对象,但每个对象Person的析构都调用了2次//子类中父类是先声明的,所以先构造父类。而析构反过来要先析构子类。//但自己不一定能保证这个析构顺序,所以不能显示调用父类析构函数。//子类析构函数结束时会自动调用父类析构函数//ChatGPT//C++ 规定,析构函数的调用顺序与构造顺序相反://1.先执行子类的析构函数体(~Derived() 的代码)。//2.再自动调用父类的析构函数(~Base())。//3.最后析构成员变量(按声明逆序析构)。//这种顺序是 编译器强制保证 的,无需程序员干预。析构必须保证逆向安全销毁//析构顺序必须严格反向(先子类后父类),如果允许手动调用父类析构://可能导致 重复析构(如果编译器之后又自动调用一次)。//破坏对象析构的安全性(如父类资源被子类依赖时提前释放)。cout << "~Student()" << endl;}
protected:int _num;//学号
};int main() {Student s1("jack", 18);Student s2(s1);Student s3("rose", 17);s1 = s3;return 0;
}第五章:继承与友元
友元关系不能继承,也就是说基类友元不能访问子类私有和保护成员
class Student;
class Person {
public:friend void Display(const Person& p, const Student& s);
protected:string _name;
};class Student : public Person {
protected:int _stuNum;
};//该函数不能访问Student的成员
void Display(const Person& p, const Student& s) {cout << p._name << endl;cout << s._stuNum << endl;
}
补充:如何实现一个不能被继承的类
//C++98 私有化父类的构造函数
class A {
public:
private:A() {}//父类私有化构造函数,子类无法创建对象//因为继承以后不可见(子类的里面外面都不能访问)
protected:int _a;int _b;
};class B : public A {
};//C++11新增final修饰父类,直接不能被继承
class A final {
public:A() {}
private:int _a;int _b;
};class B : public A {
};
第六章:继承与静态成员
基类定义了static静态成员,则整个继承体系里面只有一个这样的成员。无论派生出多少个子类,都只有一个static成员实例 。
class Person {
public:Person() { ++_count; }
protected:string _name;
public:static int _count;//统计人的个数。
};
int Person::_count = 0;
//静态成员为所有类对象所共享,不属于某个具体的对象,存放在静态区
//静态成员也是类的成员,受public、protected、private 访问限定符的限制class Student : public Person {
protected:int _stuNum;
};第七章:复杂的菱形继承及菱形虚拟继承

多继承:一个子类有两个或以上直接父类时称这个继承关系为多继承

菱形继承:菱形继承是多继承的一种特殊情况。

菱形继承的问题:从下面的对象成员模型构造,可以看出菱形继承有数据冗余和二义性的问题。在Assistant的对象中Person成员会有两份。

class Person {
public:string _name;//姓名int _age;
};class Student : public Person {
protected:int _num;//学号
};class Teacher : public Person {
protected:int _id;//职工编号
};class Assistant : public Student, public Teacher {
protected:string _majorCourse;//主修课程
};void Test() {//菱形继承的问题:菱形继承有数据冗余和二义性的问题。在Assistant的对象中Person成员会有两份。 Assistant a; //a._name = "peter";//这样会有二义性无法明确知道访问的是哪一个// 需要显示指定访问哪个父类的成员可以解决二义性问题,但是数据冗余问题无法解决a.Student::_name = "xxx";a.Teacher::_name = "yyy";
}虚拟继承可以解决菱形继承的二义性和数据冗余的问题。如上面的继承关系,在Student和Teacher的继承Person时使用虚拟继承,即可解决问题。需要注意的是,虚拟继承不要在其他地方去使用。
class Person {
public:string _name;
};class Student : virtual public Person {
protected:int _num;
};class Teacher : virtual public Person {
protected:int _id;
};class Assistant : public Student, public Teacher {
protected:string _majorCourse;
};void Test() {Assistant a;//即可指定访问,也能不指定访问a.Student::_name = "xxx";a.Teacher::_name = "yyy";a._name = "peter";
}虚拟继承解决数据冗余和二义性的原理
为了研究虚拟继承原理,我们给出了一个简化的菱形继承继承体系,再借助内存窗口观察对象成员的模型。
非虚拟继承时D的情况演示
//非虚拟继承时D的情况演示
class A {
public:int _a;
};class B : public A {
public:int _b;
};class C : public A {
public:int _c;
};class D : public B, public C {
public:int _d;
};int main() {//A:_a//B:_a, _b//C:_a, _c//D:B::_a, _b, C::_a, _c, _dD d;d.B::_a = 1;d.C::_a = 2;d._b = 3;d._c = 4;d._d = 5;return 0;
}
虚拟继承时,D的情况演示
class A {
public:int _a;
};class B : virtual public A {
public:int _b;
};class C : virtual public A {
public:int _c;
};class D : public B, public C {
public:int _d;
};int main() {D d;d._a = 1;d._b = 2;B b = d;b._a = 1;b._b = 2;return 0;
}下图是菱形虚拟继承的内存对象成员模型:这里可以分析出D对象中将A放到的了对象组成的最下面,这个A同时属于B和C,那么B和C如何去找到公共的A呢?这里是通过了B和C的两个指针,指向的一张表。这两个指针叫虚基表指针,这两个表叫虚基表。虚基表中存的偏移量。通过偏移量可以找到下面的A。

虚继承后B对象的成员内存分布

第八章:继承的总结和反思
- 很多人说C++语法复杂,其实多继承就是一个体现。有了多继承,就存在菱形继承,有了菱形继承就有菱形虚拟继承,底层实现就很复杂。所以一般不建议设计出多继承,一定不要设计出菱形继承。否则在复杂度及性能上都有问题。
- 多继承可以认为是C++的缺陷之一,很多后来的OO语言都没有多继承,如Java。
- 继承和组合
- public继承是一种is-a的关系。也就是说每个派生类对象都是一个基类对象。
- 组合是一种has-a的关系。假设B组合了A,每个B对象中都有一个A对象。
- 优先使用对象组合,而不是类继承 。
- 继承允许你根据基类的实现来定义派生类的实现。这种通过生成派生类的复用通常被称为白箱复用(white-box reuse)。术语“白箱”是相对可视性而言:在继承方式中,基类的内部细节对子类可见 。继承一定程度破坏了基类的封装,基类的改变,对派生类有很大的影响。派生类和基类间的依赖关系很强,耦合度高。
- 对象组合是类继承之外的另一种复用选择。新的更复杂的功能可以通过组装或组合对象来获得。对象组合要求被组合的对象具有良好定义的接口。这种复用风格被称为黑箱复用(black-box reuse),因为对象的内部细节是不可见的。对象只以“黑箱”的形式出现。组合类之间没有很强的依赖关系,耦合度低。优先使用对象组合有助于你保持每个类被封装。
- 实际尽量多去用组合。组合的耦合度低,代码维护性好。不过继承也有用武之地的,有些关系就适合继承那就用继承,另外要实现多态,也必须要继承。类之间的关系可以用继承,可以用组合,就用组合。
//继承
class A {
public:void func() {}
protected:int _a;
};class B : public A {
public:void f() {func();//父类的公有可以使用_a++;//父类的保护也可以使用}
protected:int _b;
};//组合
class C {
public:void func() {}
protected:int _c;
};class D {
public:void f() {cc.func();//组合类的公有可以使用//cc._c++;//组合类的保护不可以使用}
protected:C cc;int _d;
};int main() {cout << sizeof(B) << endl;//8cout << sizeof(D) << endl;//8D dd;//dd.func();//组合:dd对象不能直接调用funcB bb;bb.func();//继承:bb对象可以直接调用return 0;
}面试问题
1.多继承中指针偏移问题?下面说法正确的是()
A:p1 == p2 == p3
B:p1 < p2 < p3
C:p1 == p3 != p2
D:p1 != p2 != p3
class Base1 { public: int _b1; };
class Base2 { public: int _b2; };
class Derive : public Base1, public Base2 { public: int _d; };
int main() {Derive d;Base1* p1 = &d;Base2* p2 = &d;Derive* p3 = &d;return 0;
}
//答案:C
//先继承Base1,所以在前面。后继承Base2,最后是_d。
//Base1是Derive的第一个基类,所以Base1的子对象位于Derive对象的起始位置。
//Base2是Derive的第二个基类,它的子对象位于Base1子对象之后。
//p3直接指向Derive对象的起始地址,所以p3的值与p1相同。2. 以下程序输出结果是什么()
A:class A class B class C class D B:class D class B class C class A
C:class D class C class B class A D:class A class C class B class D
class A {
public:A(const char* s) { cout << s << endl; }~A() {}
};class B :virtual public A {
public:B(const char* s1, const char* s2) :A(s1) { cout << s2 << endl; }
};class C :virtual public A {
public:C(const char* s1, const char* s2) :A(s1) { cout << s2 << endl; }
};class D :public B, public C {
public:D(const char* s1, const char* s2, const char* s3, const char* s4) :B(s1, s2), C(s1, s3), A(s1) {cout << s4 << endl;}
};
int main() {D* p = new D("class A", "class B", "class C", "class D");delete p;return 0;
}//答案:A
//在 C++ 中,构造顺序遵循:
//虚基类(按声明顺序,深度优先)。
//直接基类(按声明顺序)。
//成员对象(按声明顺序)。
//派生类自身的构造函数。//虚基类的构造由最派生类(D)直接初始化,忽略中间类(B 和 C)对虚基类的初始化。
//由于 A 是虚基类,B 和 C 对 A 的初始化会被忽略,A 由 D 直接初始化。
//因此,构造函数的调用顺序和输出为:
//1.A("class A") → class A。
//2.B("class A", "class B") → class B(忽略 A 的初始化)。
//3.C("class A", "class C") → class C(忽略 A 的初始化)。
//4.D 的构造函数体 → class D。//虚基类 A 的构造优先于所有非虚基类(B 和 C)。
//非虚基类的顺序由 D 的继承声明顺序决定(B → C)。
//因此构造顺序是 A → B → C → D,对应选项 A。作业
1.关于继承说法正确的是( )
A.所有的类都可以被继承
B.Car(汽车)类和Tire(轮胎)类可以使用继承方式体现
C.继承是实现代码复用的唯一手段
D.狗是一种动物,可以体现出继承的思想
答案:D
A.final说明的类不能被继承
B.应该使用组合,因为Tire类跟Car类属于Has-a的关系
C.模板也是代码复用的重要手段
D.狗是动物的一种,属于is-a关系,是继承的体现
2.下面关于继承说法不正确的是( )
A.继承可以使用现有类的所有功能,并在无需重新编写原来类的情况下对这些功能进行扩展
B.继承体系中子类必须要体现出与基类的不同
C.子类对象一定比基类对象大
D.继承呈现了面相对象程序设计的层次结构,体现了有简单到复杂的认知过程
答案:C
A.这是继承的功能,也是代码复用的体现
B.继承除了吸收基类成员之外,一般还需要扩充自己的数据成员,跟基类有所不一样
C.不一定,有可能子类只是改写父类的方法而已,并没有增加其自身的数据成员,则大小一样,故错误
D.继承体现了一定的层次结构和认知过程
3.下面关于访问权限与继承权限说法不正确的是( )
A.访问权限和继承权限是不同的概念
B.访问权限和继承权限关键字上是一样的,但是出现位置不一样
C.如果是protected继承方式,基类public的成员变量能通过基类对象在类外直接访问
D.基类私有的成员变量在子类中都不能直接访问,因为没有被子类继承了
答案:D
A.两个权限控制的东西不一样
B.访问权限在类内部,继承权限在类外
C.只要是public成员对象都可以直接访问
D.基类私有成员不能直接访问不是没有被继承,而是权限问题
4.下面关于继承权限说法正确的是( )
A.派生类在继承基类时,必须明确指定继承方式
B.Class定义的类,默认的访问权限是protected
C.struct定义的类,默认访问权限是public
D.子类没有继承基类私有的成员
答案:C
A.可以不指定,默认为private
B.Class定义的类,默认的访问权限是private
C.正确,在C++中,这是struct跟class唯一的区别
D. 私有的成员继承下来了,但是在子类中不可见
5.下面代码输出结果:()
class A {
public:void f() { cout << "A::f()" << endl; }int a;
};class B : public A {
public:void f(int a) { cout << "B::f()" << endl; }int a;
};int main() {B b;b.f();return 0;
}A.打印A::f()
B.打印B::f()
C.不能通过编译,因为基类和派生类中a的类型以及名称完全相同
D.以上说法都不对
答案:D
A.错误
B.错误
C.不能通过编译是正确的,不过原因不是因为成员变量a的问题,而是子类同名隐藏了父类方法的原因
D.很显然以上说法都不对
6.关于同名隐藏的说法正确的是( )
A.同一个类中,不能存在相同名称的成员函数
B.在基类和子类中,可以存在相同名称但参数列表不同的函数,他们形成重载
C.在基类和子类中,不能存在函数原型完全相同的函数,因为编译时会报错
D.成员函数可以同名,只要参数类型不同即可,成员变量不能同名,即使类型不同
答案:D
A.可以存在,如函数重载
B.基类与子类函数名字相同,参数不同,形成的是隐藏
C.可以共存
D.成员函数在同一个类里面同名,此时构成了重载,但变量一定不能同名,故正确
7.关于派生类构造函数与析构函数说法正确的是( )
A.在派生类对象构造时,先调用基类构造函数,后调用子类构造函数
B.在派生构造函数初始化列表的位置必须显式调用基类构造函数
C.在派生类对象销毁时,先调用基类析构函数,后调用子类析构函数
D.派生类的析构函数只需析构派生类的资源即可
答案:A
A.先构造父类,在构造子类 故正确
B.不一定,如果父类有默认构造函数就不需要
C.刚好相反,先调用子类,在调用父类
D.派生类的析构函数往往还需要连同父类析构函数一起调用,同时清除父类的资源
8.下列代码中f函数执行结束后输出( )
class A {
public:A() { cout << "A::A()" << endl; }~A() { cout << "A::~A()" << endl; }int a;
};class B : public A {
public:B() { cout << "B::B()" << endl; }~B() { cout << "B::~B()" << endl; }int b;
};void f() {B b;
}A.B::B() B::~B()
B.B::B() A::A() A::~A() B::B()
C.A::A() B::B() B::~B() A::~A()
D.以上都不对
答案:C
分析: 子类实例化对象,由于继承的有父类。所以会先构造父类,然后在构造子类,析构顺序完全按照构造的相反顺序进行析构,故答案为 C
9.下面说法正确的是( )
A.派生类构造函数初始化列表的位置必须显式调用基类的构造函数,已完成基类部分成员的初始化
B.派生类构造函数先初始化子类成员,再初始化基类成员
C.派生类析构函数不会自动析构基类部分成员
D.子类构造函数的定义有时需要参考基类构造函数
答案:D
A.如果父类有默认构造函数,此时就不需要
B.顺序相反,先初始化父类,再是子类
C.会调用,并且按照构造的相反顺序进行调用
D.是的,需要看父类构造函数是否需要参数子类的,从而你决定子类构造函数的定义
10.关于基类哪些成员被子类继承说法不正确的是( )
A.静态成员函数
B.所有成员变量
C.基类的友元函数
D.静态成员变量在整个继承体系中只有一份
答案:C
A.静态成员函数也可以被继承
B.成员变量所有的都会被继承,无论公有私有
C.友元函数不能被继承,相当于你爹的朋友不一定是你的朋友
D.静态成员属于整个类,不属于任何对象,所以在整体体系中只有一份
11.关于以下菱形继承说法不正确的是( )
class B { public: int b; };
class C1 : public B { public: int c1; };
class C2 : public B { public: int c2; };
class D : public C1, public C2 { public: int d; };A.D总共占了20个字节
B.B中的内容总共在D对象中存储了两份
C.D对象可以直接访问从基类继承的b成员
D.菱形继承存在二义性问题,尽量避免设计菱形继承
答案:C
A.C1中b和c1共8个字节,C2中c2和b共8个字节,D自身成员d 4个字节,一共20字节
B.由于菱形继承,最终的父类B在D中有两份
C.子类对象不能直接访问最顶层基类B中继承下来的b成员,因为在D对象中,b有两份,一份是从C1中继承的,一份是从C2中继承的,直接通过D的对象访问b会存在二义性问题,在访问时候,可以加类名::b,来告诉编译器想要访问C1还是C2中继承下来的b。
D.菱形继承存在二义性问题,尽量避免设计菱形继承,如果真有需要,一般采用虚拟继承减少数据冗余
12. 下面哪项结果是正确的( )
class Base1 { public: int _b1; };
class Base2 { public: int _b2; };class Derive : public Base1, public Base2 {
public: int _d;
};int main() {Derive d;Base1* p1 = &d;Base2* p2 = &d;Derive* p3 = &d;return 0;
}A.p1 == p2 == p3
B.p1 < p2 < p3
C.p1 == p3 != p2
D.p1 != p2 != p3
答案:C
分析:p1和p2虽然都是其父类,但在子类内存模型中,其位置不同,所以p1和p2所指子类的位置也不相同,因此p1!=p2,
由于p1对象是第一个被继承的父类类型,所有其地址与子类对象的地址p3所指位置都为子类对象的起始位置,因此p1==p3,所以C正确
13.关于基类与子类对象之间赋值说法不正确的是( )
A.基类指针可以直接指向子类对象
B.基类对象可以直接赋值给子类对象
C.子类对象的引用不能引用基类的对象
D.子类对象可以直接赋值给基类对象
答案:B
A.这是赋值兼容规则的其中一条,正确
B.基类不能给子类对象直接赋值,因为父类类型对于子类类型来说类型不完全,故错误
C.不能用父类初始化子类引用
D.这也是赋值兼容规则的其中一条
14.关于基类与派生类对象模型说法正确的是()
A.基类对象中包含了所有基类的成员变量
B.子类对象中不仅包含了所有基类成员变量,也包含了所有子类成员变量
C.子类对象中没有包含基类的私有成员
D.基类的静态成员可以不包含在子类对象中
E.以上说法都不对
答案:E
A.静态变量就不被包含
B.同理,静态变量就不被包含
C.父类所有成员都要被继承,因此包含了
D.静态成员一定是不被包含在对象中的
E.很显然,以上说法都不正确
