手表网站背景猎头网站 做猎头的流程
ATAC-seq在植物研究领域的应用我们已经介绍2期了,本期我们聚焦ATAC-seq技术在果实发育方向的应用案例。
· 植物ATAC-seq文献集锦(一)——基因组篇
· 植物ATAC-seq文献集锦(二)——生长发育篇
文献一:Identification and functional characterization of conserved cis-regulatory elements responsible for early fruit development in cucurbit crops

-
中文标题:瓜类作物果实早期发育保守顺式调控元件的鉴定与功能表征
-
发表时间:2024.02
-
发表期刊:plant cell(IF:11.6)
-
研究物种:6种葫芦科作物(黄瓜、西瓜、甜瓜、南瓜、丝瓜和葫芦)
-
研究技术:比较基因组学、ATAC-seq、RNA-seq、CRISPR/Cas9基因编辑
-
主要内容:
本研究通过比较基因组学、ATAC-seq技术、RNA-seq分析和CRISPR/Cas9基因编辑技术,深入探究了6种葫芦科作物(黄瓜、西瓜、甜瓜、南瓜、丝瓜和葫芦)早期果实发育中的保守顺式调控元件(CREs)。研究团队鉴定了大量保守非编码序列(CNSs),包括特定于葫芦科的CNSs,并分析了这些序列与染色质可及性的关系。通过整合CNSs和ACRs(可访问染色质区域)的数据,研究人员揭示了一系列可能调控关键基因表达的CNSs,并实验验证了这些CNSs在调控果实发育中的作用。这些发现不仅为理解葫芦科作物果实发育的分子机制提供了新的视角,而且为未来的作物改良提供了潜在的基因编辑靶点。
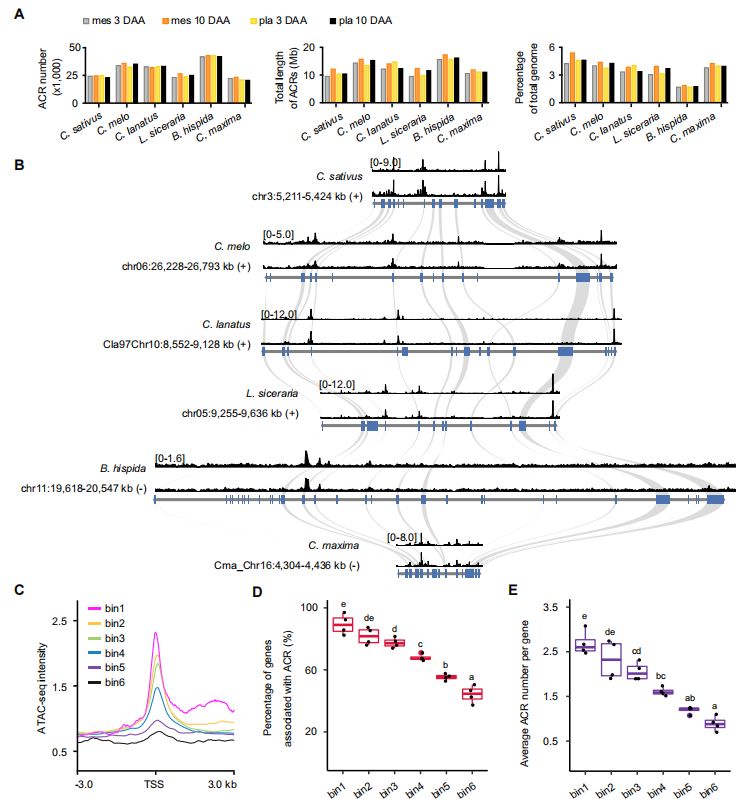
Fig1. 6种瓜类作物两个关键时期两个组织中ACRs的鉴定与特性分析
文献二:Multiomics analyses of the effects of LED white light on the ripening of apricot fruits

-
中文标题:LED白光对杏果实成熟影响的多组学分析
-
发表时间:2024.01
-
发表期刊:Journal of Advanced Research(IF:10.7)
-
研究物种:杏
-
研究技术:ATAC-seq、RNA-seq、代谢组
-
主要内容:
本研究利用多组学分析方法,包括代谢组学、转录组学和ATAC-Seq,探究了LED白光处理对杏果实成熟过程中生理和营养品质的影响,以及对果实转录调控和代谢物变化的作用。研究发现,LED白光处理能够激活与抗坏血酸和糖醛酸代谢、黄酮类生物合成相关的代谢途径,并影响与植物激素信号传导、果实质地和颜色转变以及植物抗氧化活性相关的基因表达。通过综合分析差异基因、代谢物和开放染色质区域,研究构建了一个网络模型,阐释了LED影响杏果实成熟后成熟和衰老的潜在调控机制。研究结果为理解LED光照对果实成熟过程中品质变化的调控机制提供了新见解,并为延长其他水果和蔬菜的货架寿命提供了一种有前景的方法。

Fig2.杏果实成熟的ATAC-seq数据概述
文献三:Transcriptional Landscape and Dynamics Involved in Sugar and Acid Accumulation during Apple Fruit Development

-
中文标题:苹果果实发育过程中糖和酸积累的转录景观和动态
-
发表时间:2024.05
-
发表期刊:Plant Physiology(IF:7.4)
-
研究物种:苹果
-
研究技术:生理指标检测、ATAC-seq、RNA-seq
-
主要内容:
本文通过结合ATAC-seq和RNA-seq技术,深入研究了苹果果实发育过程中糖分和酸度积累的转录调控机制。研究团队对苹果“Changfu 2”品种的8个发育阶段进行了生理指标测量,并通过转录组测序分析了与糖分和有机酸代谢相关的基因表达。利用 WGCNA分析揭示了与糖分积累相关的基因模块,并通过ATAC-seq技术探究了染色质可及性的动态变化。此外,研究还预测并验证了多个可能调控糖分和酸度积累的关键转录因子,构建了一个转录调控网络,为识别控制这些品质特性的候选基因提供了平台。这些发现不仅增进了我们对苹果果实发育过程中调控机制的理解,而且为苹果品质改良提供了科学依据。
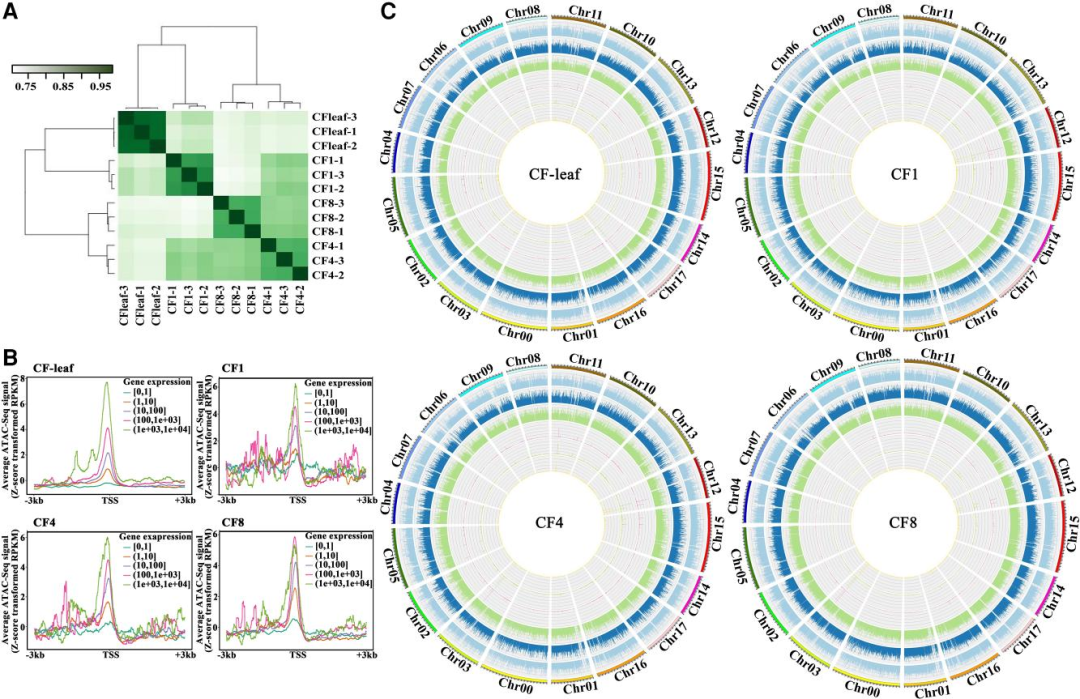
Fig3.苹果叶片和果实发育3个阶段的12个文库的ATAC-seq分析
文献四:The regulatory mechanisms of delayed senescence of nitric oxide treatment of hyacinth beans

-
中文标题:一氧化氮处理延缓扁豆衰老的转录组学、代谢组学和染色质可及性研究
-
发表时间:2023.01
-
发表期刊:Postharvest Biology and Technology(IF:7.0)
-
研究物种:扁豆
-
研究技术:ATAC-seq、RNA-seq、代谢组
-
主要内容:
本研究通过外源一氧化氮(NO)处理扁豆,利用代谢组学、转录组学和ATAC-seq分析技术,探究了NO对扁豆衰老的影响。研究发现,NO处理能够显著影响扁豆中的代谢物积累,特别是黄酮类化合物和酚酸类化合物,同时抑制了与细胞壁降解、木质素合成、植物-病原体互作以及乙烯信号转导相关的基因表达。ATAC-seq分析揭示了14个富集的转录因子,这些转录因子可能在调控豆类衰老中发挥作用。综合来看,NO通过调节黄酮类代谢、细胞壁降解、木质素合成、植物激素、黄酮类生物合成、植物-病原体互作基因以及ERF/DREB转录因子家族,从而延缓了扁豆的衰老过程。研究结果为理解NO在调控豆类衰老过程中的作用机制提供了新的见解,并为延长豆类的采后保鲜期提供了理论基础。

Fig4.ATAC-seq分析
文献五:ATAC-seq and RNA-seq reveal the role of AGL18 in regulating fruit ripeningvia ethylene-auxin crosstalk in papaya

-
中文标题:ATAC-seq和RNA-seq联合揭示了AGL18在乙烯-生长素调节果实成熟中的作用
-
发表时间:2022.05
-
发表期刊:Postharvest Biology and Technology(IF:6.751)
-
研究物种:番木瓜
-
研究技术:ATAC-seq、RNA-seq、亚细胞定位、Y1H、双荧光素酶报告基因实验、ChIP-qPCR、EMSA
-
主要内容:
本文通过ATAC-seq和RNA-seq技术手段,研究了木瓜成熟过程中染色质可及性和基因表达的变化,特别关注了乙烯和生长素信号途径之间的相互作用。研究揭示了转录因子CpAGL18在木瓜成熟过程中的关键作用,该因子通过整合乙烯和生长素信号来调控果实软化和成熟。通过1-MCP处理,研究者观察到CpAGL18的表达在自然成熟条件下显著增加,但在长期1-MCP处理下受到强烈抑制。此外,通过EMSA、Y1H和ChIP-qPCR等实验技术,验证了CpAGL18在体内外与CpACS1和CpSAUR32启动子的结合,并激活了这些启动子。这些发现为理解木瓜成熟调控机制提供了新的见解,并为改善果实品质和延长采后货架寿命提供了潜在的分子靶点。
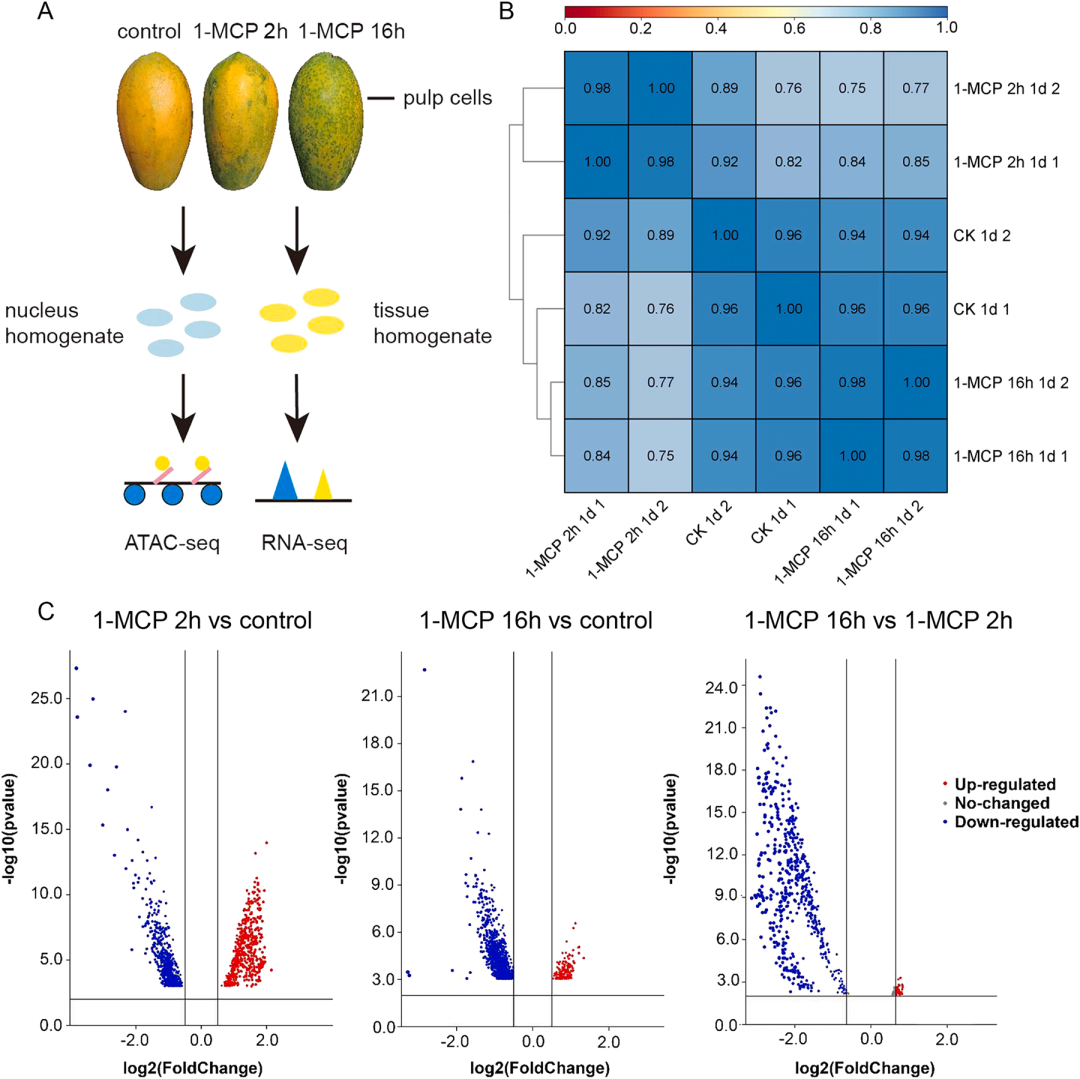
Fig5.1-MCP诱导的染色质可及性改变
文献六:Integrated metabolic, transcriptomic and chromatin accessibility analyses provide novel insights into the competition for anthocyanins and flavonols biosynthesis during fruit ripening in red apple.

-
中文标题:综合代谢、转录组学和染色质可及性分析为红苹果果实成熟过程中花青素和黄酮醇生物合成的竞争提供了新的见解
-
发表时间:2022.09
-
发表期刊:Front Plant Science(IF:5.6)
-
研究物种:苹果
-
研究技术:代谢组、RNA-Seq、ATAC-Seq、qRT-PCR
-
主要内容:
本研究通过综合分析红苹果‘Hongmantang’品种在三个成熟阶段(PS1、PS5和PS9)的代谢组、转录组和染色质可及性,探究了苹果果实成熟过程中花青素和黄酮醇生物合成的竞争机制。研究发现,在成熟过程中,某些代谢物如氨基酸衍生物、有机酸、核苷酸及其衍生物和单宁主要在PS1阶段积累并在随后的成熟阶段减少,而糖类和醇类、维生素和二苯乙烯类代谢物则随成熟过程增加。特别地,花青素和黄酮醇的生物合成显示出动态竞争关系。结构基因如FLSs和DFRs的差异表达在两种黄酮类化合物的积累中起了主要作用。MYB和bZIP基因的染色质可及性和表达变化预测了它们在调节花青素和黄酮醇生物合成中发挥主导作用。研究结果为理解红苹果果实成熟过程中代谢物变化的分子机制提供了新的见解。
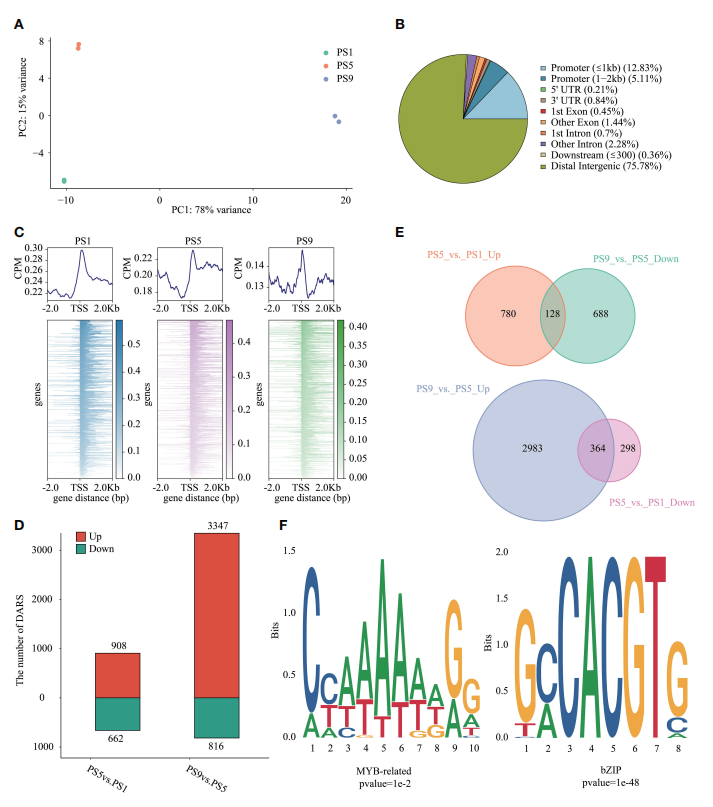
Fig6.红苹果果实成熟过程中染色质可及性特征
文献七:Increasing Fruit Weight by Editing a Cis-Regulatory Element in Tomato KLUH Promoter Using CRISPR/Cas9.

-
中文标题:利用CRISPR/Cas9编辑番茄KLUH启动子顺式调控元件增加果实重量
-
发表时间:2022.04
-
发表期刊:Front Plant Science(IF:5.6)
-
研究物种:番茄
-
研究技术:CRISPR/Cas9基因编辑、表型分析、qRT-PCR、ATAC-seq
-
主要内容:
本研究通过CRISPR/Cas9基因编辑技术,针对番茄KLUH基因启动子中的一个单核苷酸多态性(SNP)位点进行编辑,该位点与果实重量高度相关。研究人员利用同源性预测和ATAC-seq分析,确定了一个保守的顺式调控元件(CRE),并使用CRISPR/Cas9系统在番茄中产生了21个不同的突变等位基因。其中五个突变等位基因(m2+4bp、m3+1bp、m5−1bp、m13−8bp和m14−9bp)在所有实验评估中均显示出果实重量的一致性增加,以及小果比例的显著减少。特别是m2+4bp和m3+1bp纯合子显著增加了果实重量,分别为10.7–15.7%和8.7–16.3%。此外,研究还发现这些有益等位基因增加了所有果实位置的重量。研究表明,通过CRISPR/Cas9介导的顺式工程可以有效地改善番茄等作物的产量,为作物改良提供了新的策略。
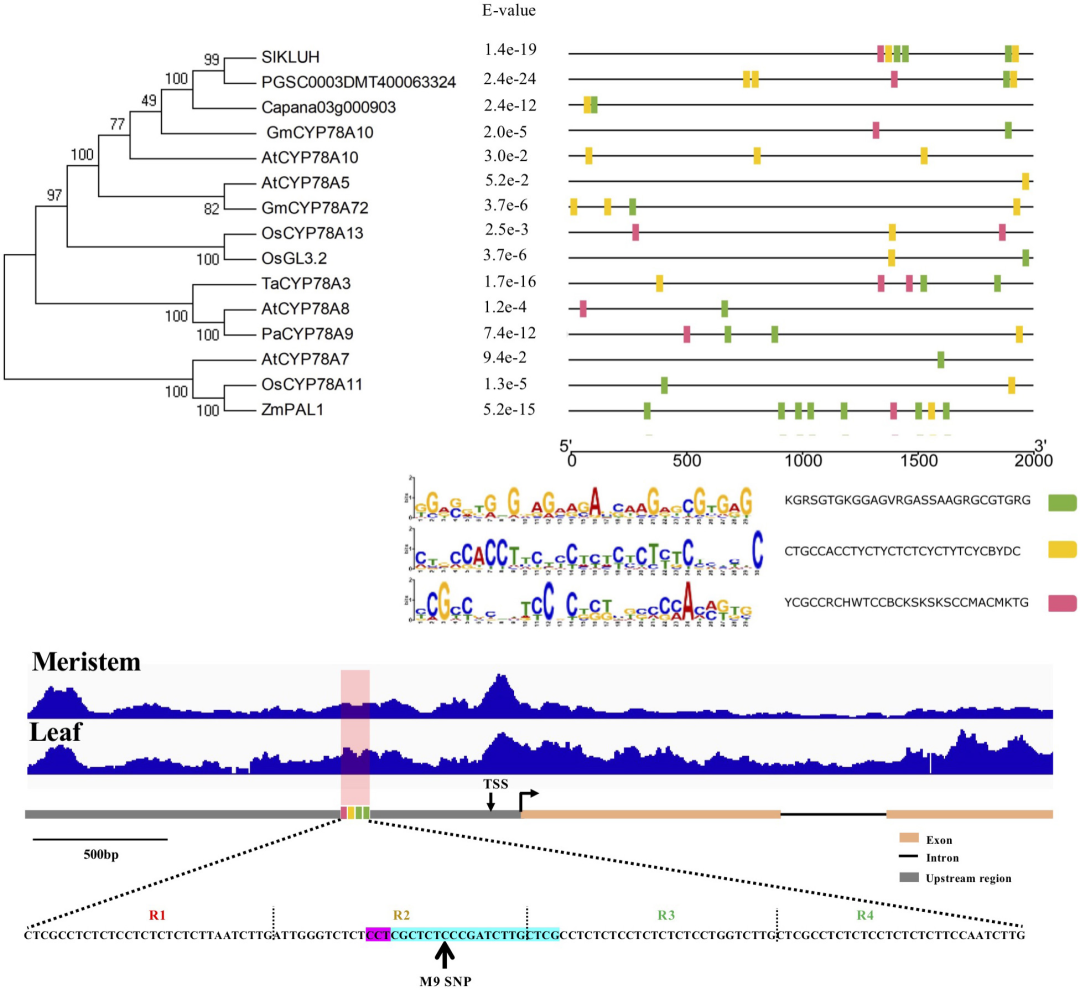
Fig7.利用同源性预测和ATAC-seq鉴定SlKLUH启动子中假定的顺式调控元件
总 结
随着生物技术的发展,尤其是ATAC-seq技术的应用,我们对植物果实发育的分子机制有了更深入的理解。本文献集锦通过展示一系列创新性研究,揭示了ATAC-seq技术在解析果实发育过程中染色质可及性变化、基因表达调控以及代谢途径调控等方面的重要价值。这些研究成果不仅丰富了我们对植物果实发育生物学的知识体系,而且为作物品质改良和采后保鲜提供了新的策略和分子靶点。
爱基自荐
爱基百客拥有丰富的ATAC-seq项目经验,致力于为您提供最专业、最可靠的ATAC-seq技术服务。无论动物,还是植物和真菌的研究,我们都能为您量身定制最优化的实验方案,解决您在样品处理、数据分析和结果展示等方面的技术难题。选择爱基百客,选择专业、选择信赖!让我们携手合作,共同探索基因调控的奥秘,开启科研之旅的新篇章!赶快联系我们,了解更多关于ATAC技术的信息吧!
· ATAC-seq产品介绍 ·
ATAC-seq广泛用于染色质开放性研究,该技术利用Tn5转座酶可以接近核小体疏松区域切割暴露的DNA,获得开放染色质区段(open chromatin),然后结合高通量测序和生物信息学分析来挖掘潜在的活跃转录因子及其靶基因,以此探究生物学相关问题。
· 技术优势:
1. 新鲜组织/细胞文库极速交付,最快可当天交付待测序文库;
2. 针对于新鲜样本,提供针对性运输方案,以满足细胞活性;
3. 项目经验丰富,除了常规模式动植物,拥有丰富的疑难样本实验经验,满足客户的不同需求。
4. 拥有完善的ATAC-seq配套分析流程(标准分析+关联分析),丰富的个性化分析。
5. 已协助客户在Nature Commun、Plant Commun和Physiol Plant等国际知名刊物发表多篇高水平文章。
6. 提供从实验设计,建库测序,到数据分析和验证(酵母单杂、EMSA、ChIP等)一站式服务。

· 实测数据:
Reads密度分布图
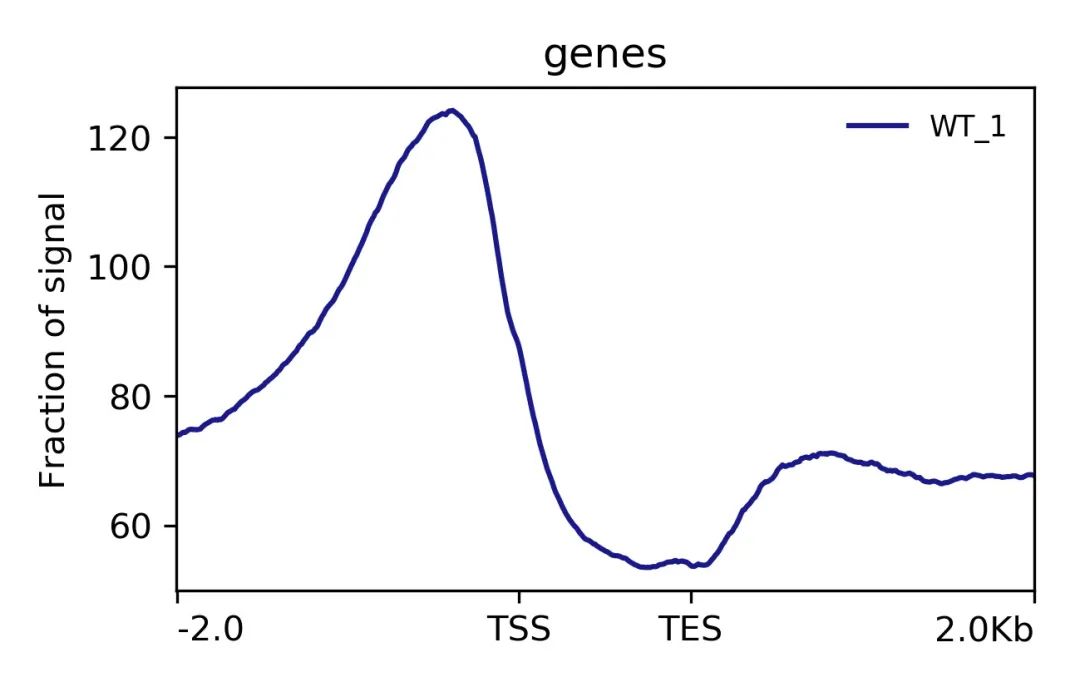
真菌菌丝Reads密度分布图
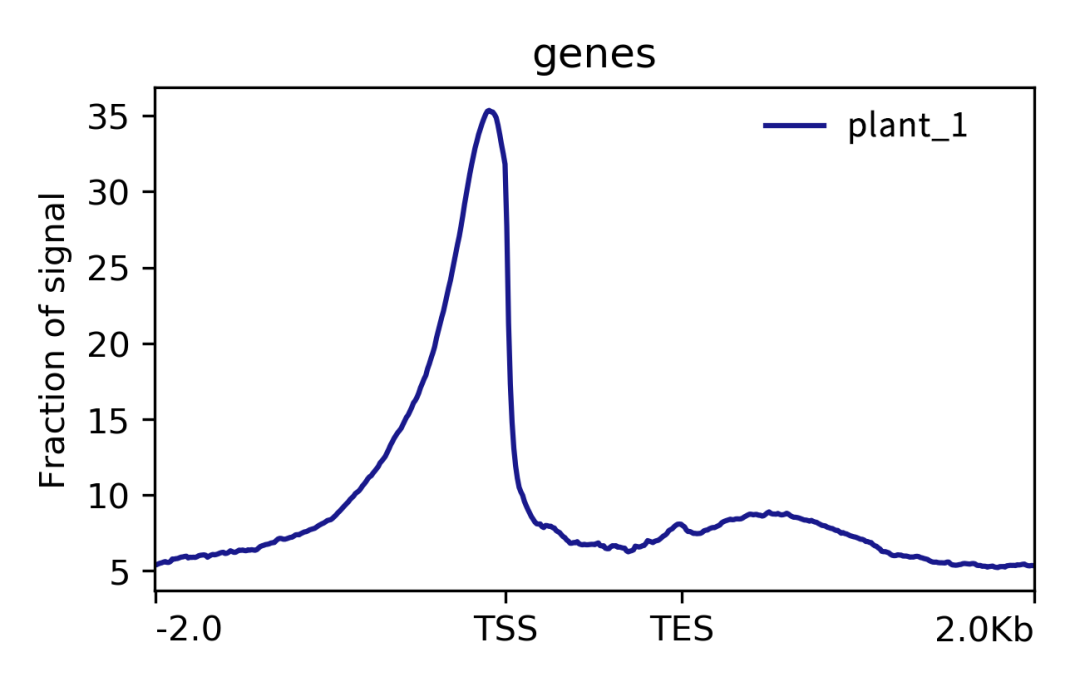
植物组织Reads密度分布图
Peak可视化
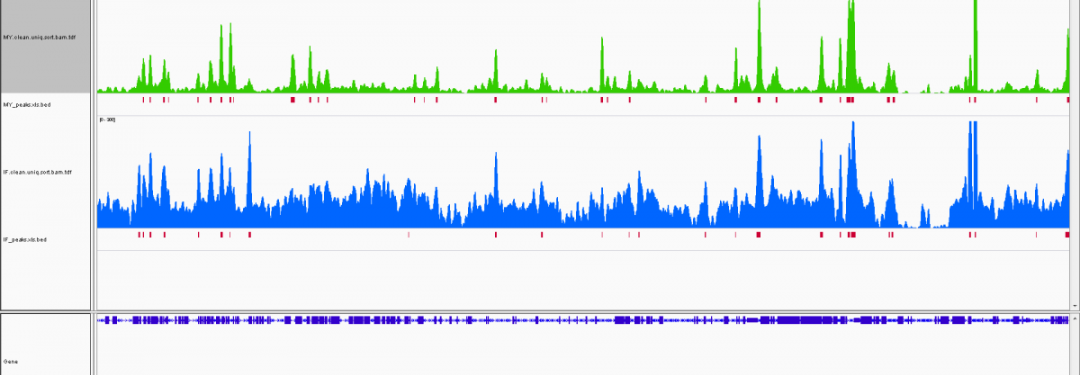
疫霉菌样本
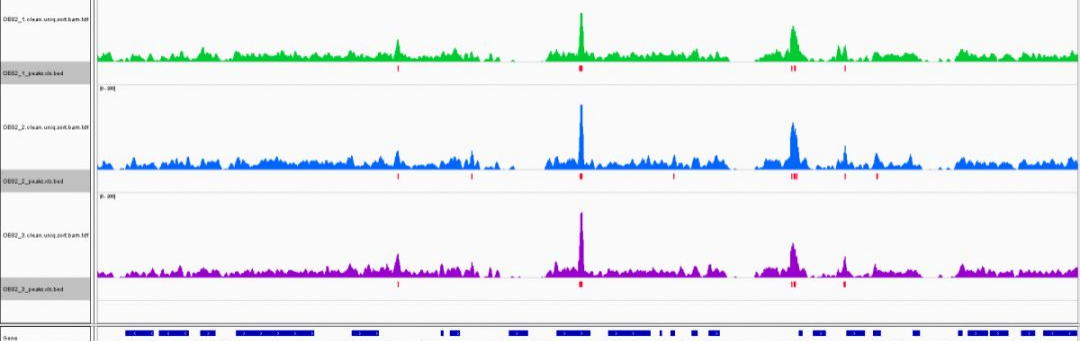
水稻样本