网站制作超链接怎么做工作室注册流程
wx供重浩:创享日记
对话框发送:转向桥
获取完整报告说明书+工程源文件
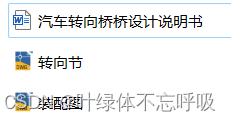
转向节图
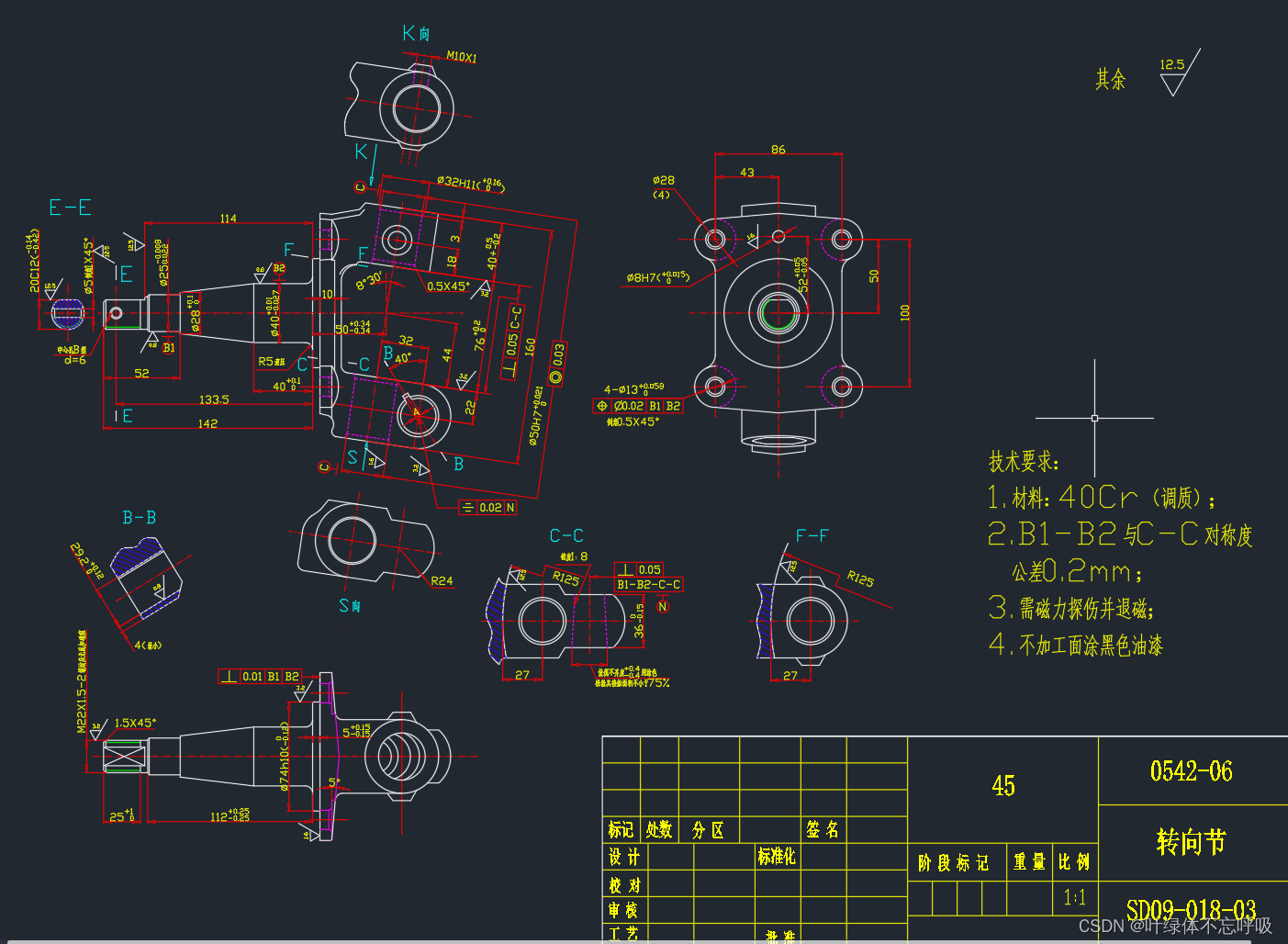
装配图
本文设计的是JY1061A型采用前置后轮驱动的载货汽车转向桥,因此该转向桥为从动桥。从动桥的功用:从动桥也称非驱动桥,又称从动车轴。它通过悬架与车架(或承载式车身)相联,两端安装从动车轮,用以承受和传递车轮与车架之间的力(垂直力、纵向力、横向力)和力矩。并保证转向轮作正确的转向运动。
1、设计要求:
(1)保证有足够的强度:以保证可靠的承受车轮与车架之间的作用力。
(2)保证有足够的刚度:以使车轮定位参数不变。
(3)保证转向轮有正确的定位角度:以使转向轮运动稳定,操纵轻便并减轻轮胎的磨损。
(4)转向桥的质量应尽可能小:以减少非簧上质量,提高汽车行驶平顺性。
通过对CJ1061A型前桥的设计,可以加深我们的设计思想,即:
(1)处理好设计的先进性和生产的可能性之间的关系;
(2)协调好产品的继承性和产品的“三化”之间的关系。
2、结构参数选择
JY1061A型汽车总布置整车参数见表1:
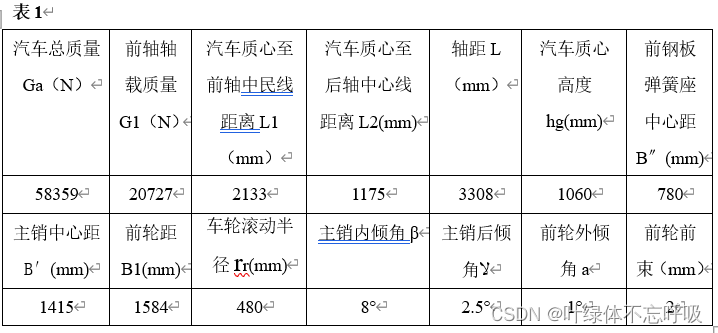
2.1、转向桥结构形式
本前桥采用非断开式转向桥
2.2、选择前桥结构型式及参数
(1)前轴结构形式:工字形断面加叉形转向节主销固定在前轴两端的拳部里。
(2)转向节结构型式:整体锻造式。
(3)主销结构型式:圆柱实心主销。
(4)转向节止推轴承结构形式:止推滚柱轴承。
(5)主销轴承结构形式:滚针轴承
(6)轮毂轴承结构形式:单列向心球轴承
2.3、前轮定位角
本型前轮定位角选择见 ‘表1’
二、转向桥强度计算
1、前轴强度计算
1.1、前轴受力简图
如图1所示:
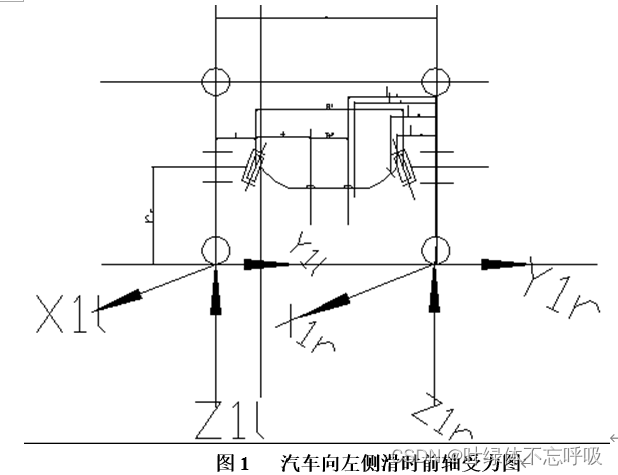
(其余完整详见下载!)
(其余完整详见下载!)


转向桥是利用转向节使车轮偏转一定的角度以实现汽车的转向,同时还承受和传递汽车与车架及车架之间的垂直载荷、 纵向力和侧向力以及这些力形成的力矩。转向桥通常位于汽车的前部,因此也常称为前桥。
各类汽车的转向桥结构基本相同,主要有前轴(梁)、转向节、主销和轮毂
(1)前轴:由中碳钢锻造,采用抗弯性较好的工字形断面。为了提高抗扭强度,接近两端略呈方形。前轴中部下凹使发动机的位置得以降低,进而降低汽车质心,扩展驾驶员视野,减小传动轴与变速器输出轴之间的夹角。下凹部分的两端制有带通孔的加宽平面,用以安装钢板弹簧。前轴两端向上翘起,各有一个呈拳形的加粗部分,并制有通孔。
(2)主销:即插入前轴的主销孔内。为防止主销在孔内转动,用带有螺纹的楔形销将其固定。
(3)转向节:转向节上的两耳制有销孔,销孔套装在主销伸出的两端头,使转向节连同前轮可以绕主销偏转,实现汽车转向。为了限制前轮最大偏转角,在前轴两端还制有最大转向角限位凸块(或安装限位螺钉)。
转向节的两个销孔,要求有较高的同心度,以保证主销的安装精度和转向灵活。为了减少磨损,在销孔内压入青铜或尼龙衬套。衬套上开有润滑油槽,由安装在转向节上的油嘴注入润滑脂润滑。为使转向灵活轻便,还在转向节下耳的上方与前轴之间装有推力轴承11;在转向节上耳与前轴之间,装有调整垫片8,用以调整轴向间隙。
左转向节的上耳装有与转向节臂9制成一体的凸缘,在下耳上装有与转向节下臂制成一体的凸缘。两凸缘上均制有一矩形键与左转向节上、下耳处的键槽相配合,转向节即通过矩形键及带有键形套的双头螺栓与转向节上下臂连接。
(4)轮毂:轮毂通过内外两个滚锥轴承套装在转向节轴颈上。轴承的松紧度可以由调整螺母调整,调好后的轮毂应能正、反方向自由转动而无明显的摆动。然后用锁紧垫圈锁紧。在锁紧垫圈外端还装有止推垫圈和锁紧螺母,拧紧后应把止推垫圈弯曲包住锁紧螺母或用开口销锁住,以防自行松动。
轮毂外端装有冲压的金属端盖,防止泥水或尘土浸入。轮毂内侧装有油封 (有的油封装在转向节轴颈的根部),有的还装有挡油盘。一旦油封失效,则外面的挡油盘仍可防止润滑脂进入制动器内。
