网站建设设计官网电商详情页设计模板
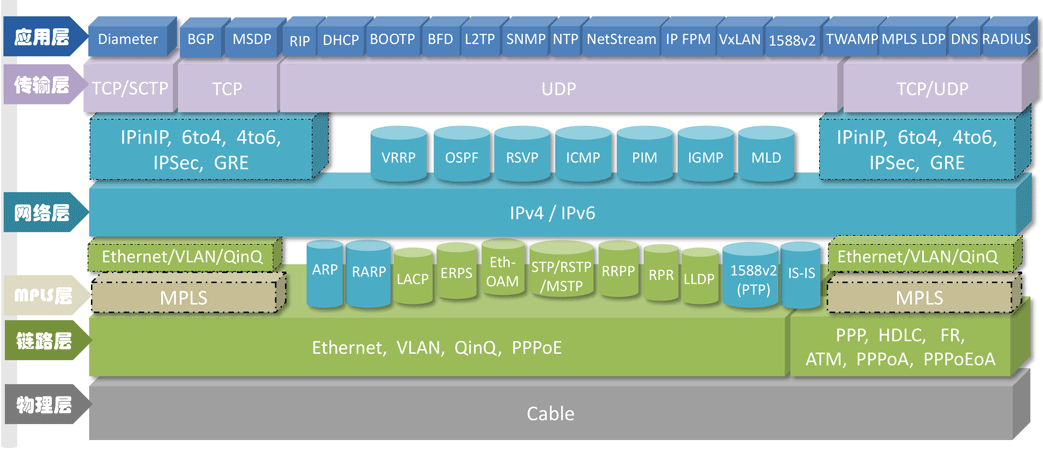
最近在回顾网络知识点的时候,发现华为数通有关报文格式及网络协议地图神仙网站,这里涵盖了各个协议层及每个协议层对应的协议内容,最人性的化的一点是点击每个单独的协议可以跳转到该协议详细报文格式页面,有对应的说明和解释,对初学者或者巩固者等都有很大的帮助;当然该内容也支持华为的ICS Lite小工具进行离线下载并查看,相关链接如下:
链接地址1:Info-Finder(在线工具) 报文格式
链接地址2:IP 报文格式大全
来吧展示:
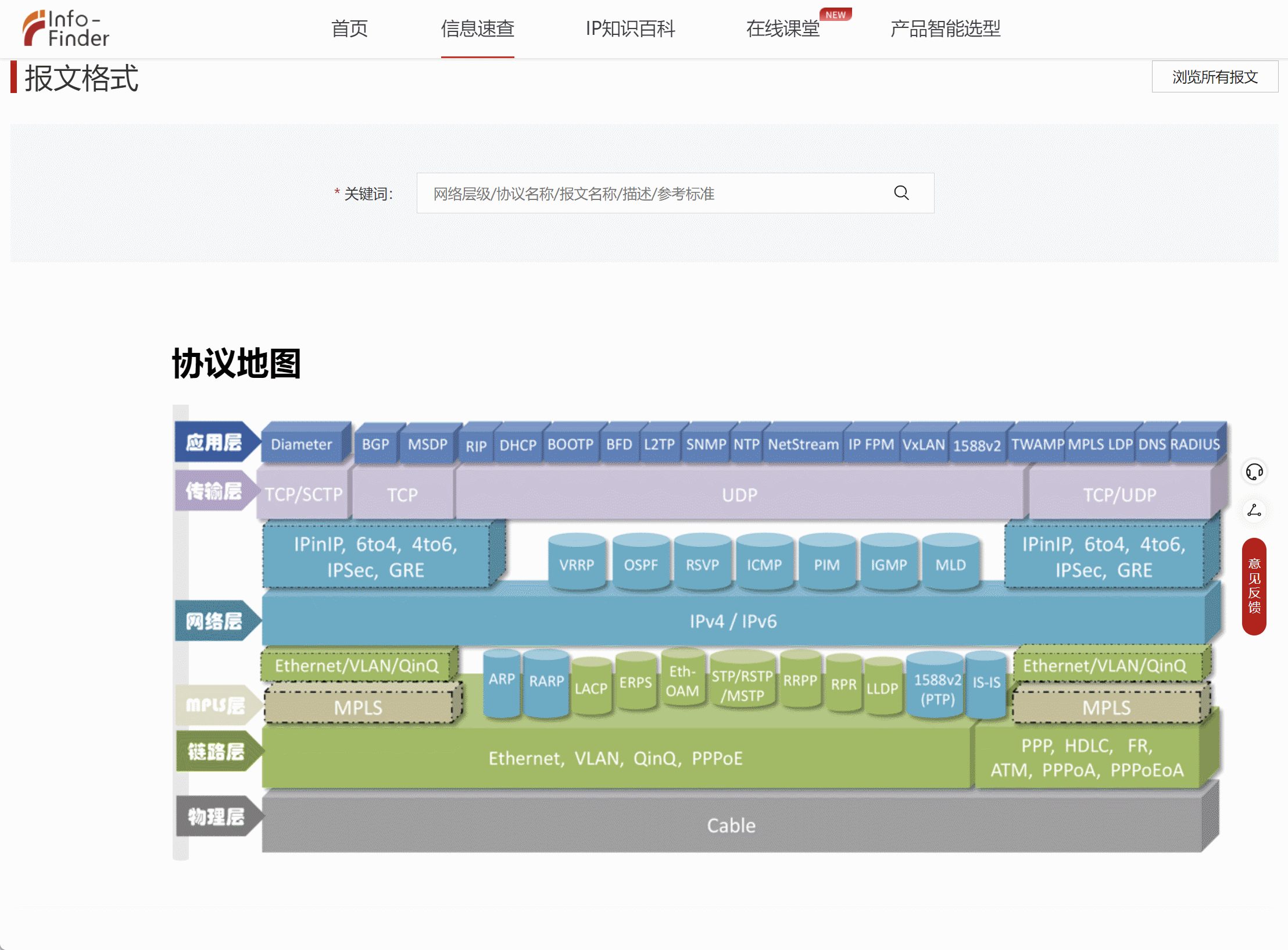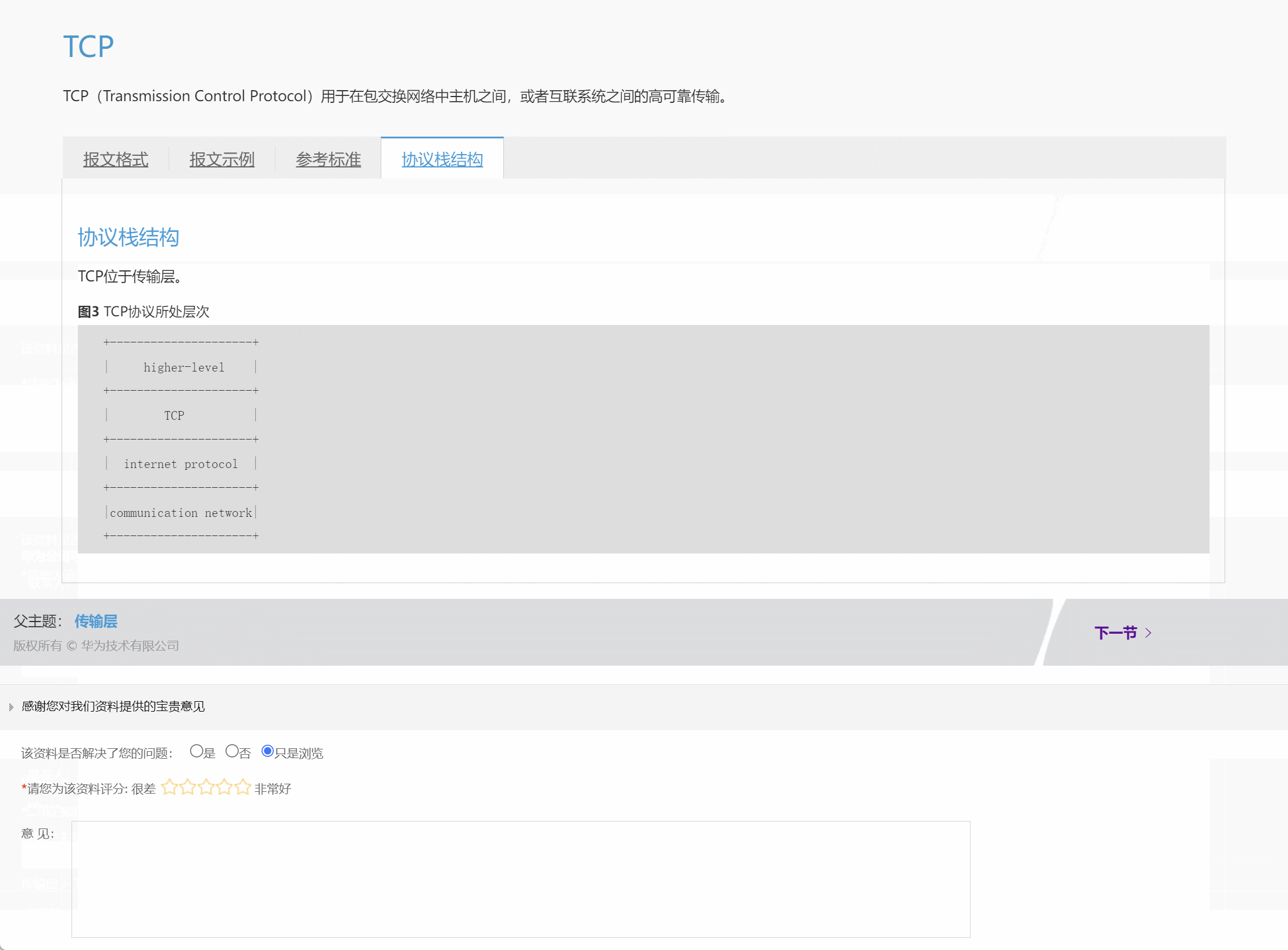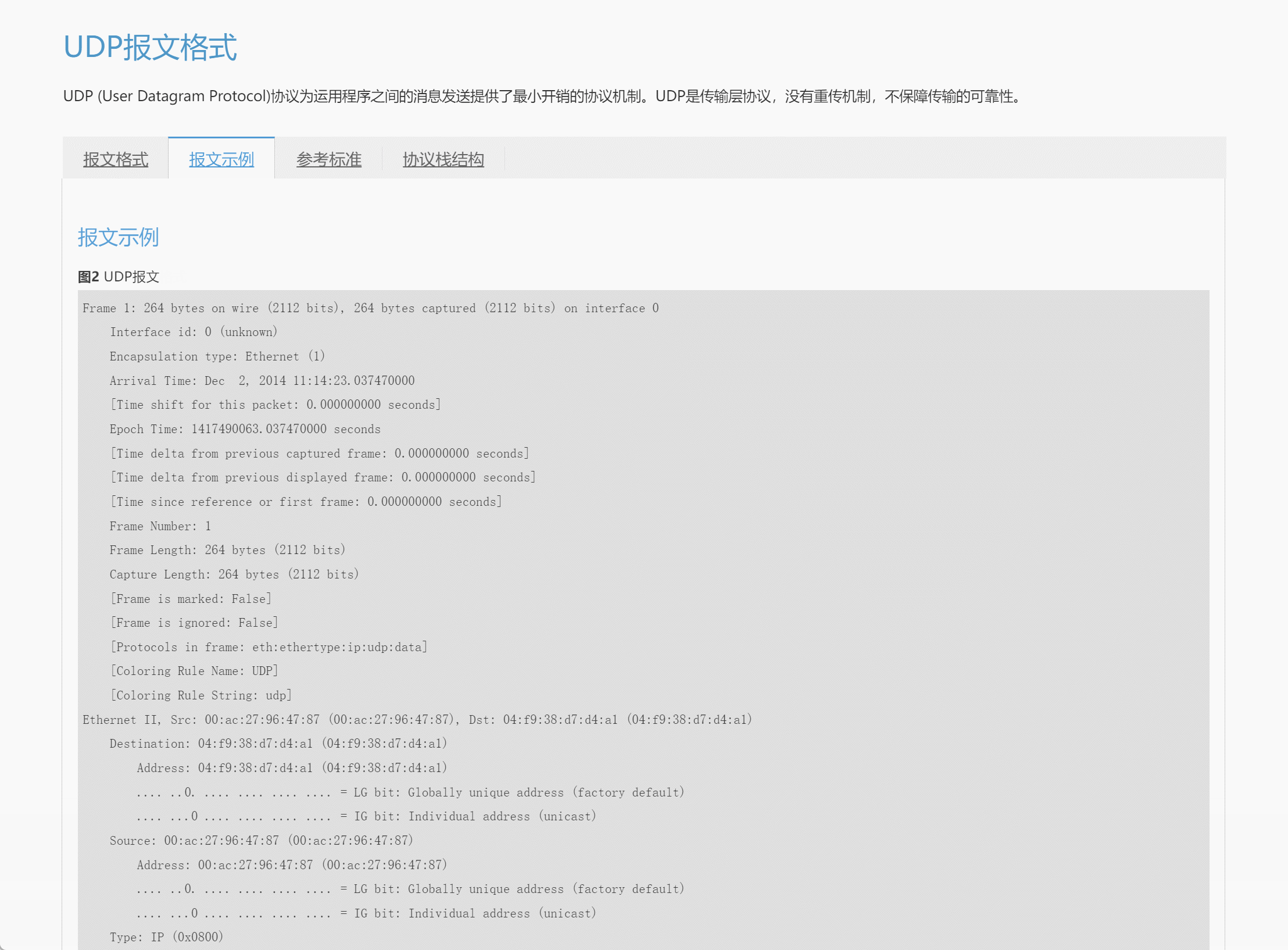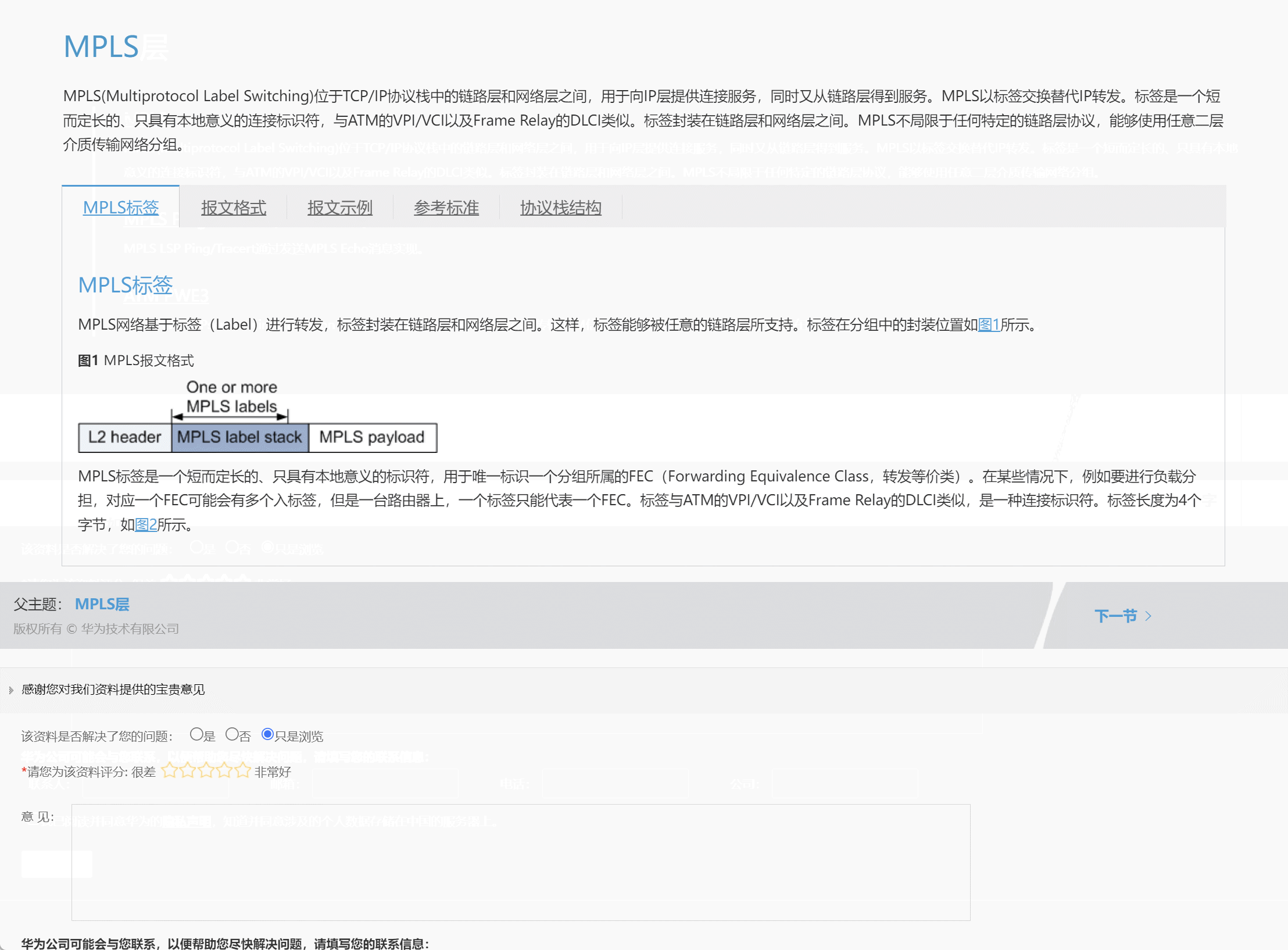
最近在回顾网络知识点的时候,发现华为数通有关报文格式及网络协议地图神仙网站,这里涵盖了各个协议层及每个协议层对应的协议内容,最人性的化的一点是点击每个单独的协议可以跳转到该协议详细报文格式页面,有对应的说明和解释,对初学者或者巩固者等都有很大的帮助;当然该内容也支持华为的ICS Lite小工具进行离线下载并查看,相关链接如下:
链接地址1:Info-Finder(在线工具) 报文格式
链接地址2:IP 报文格式大全

来吧展示:
