企业买好域名后怎么做网站设计页面图片
一、项目介绍
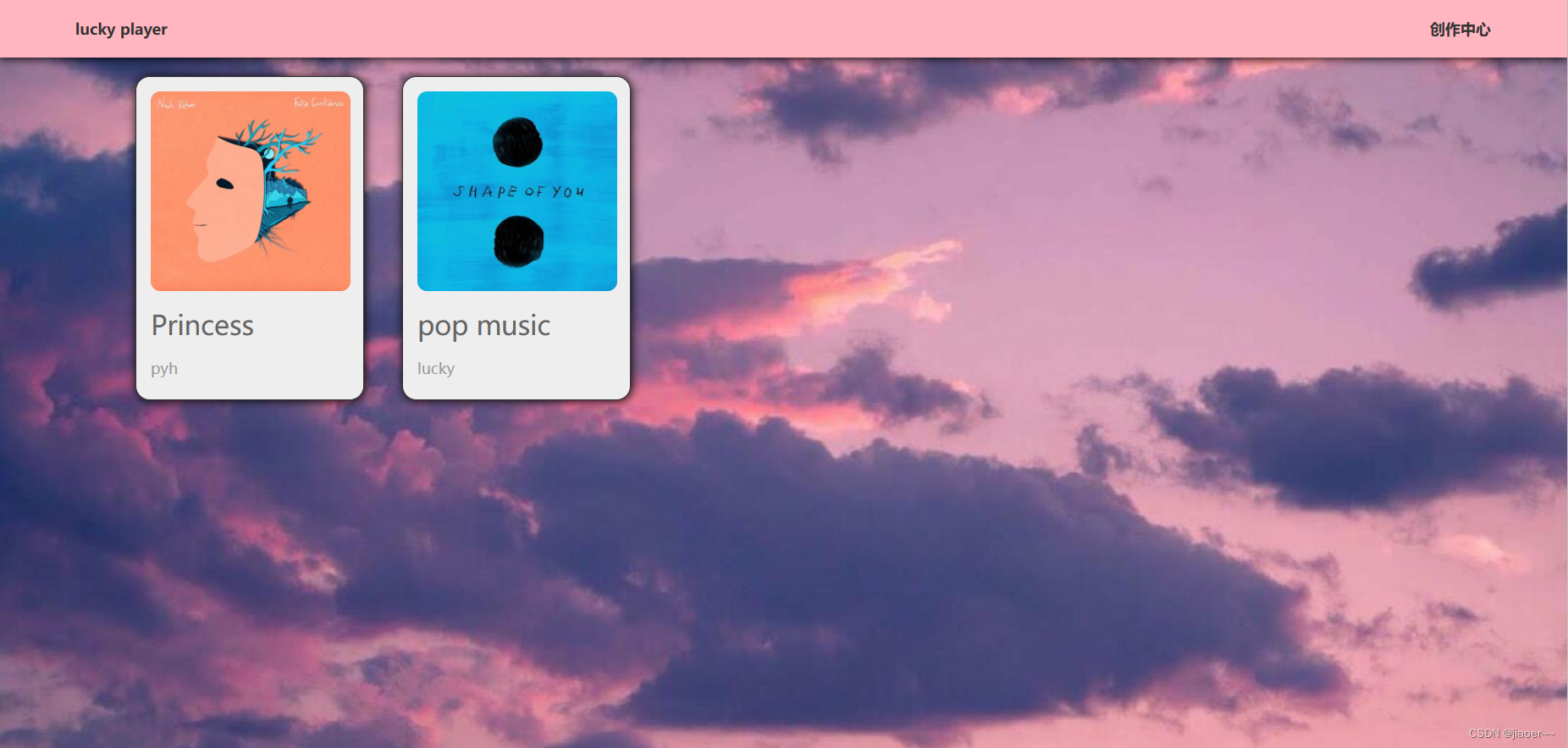
项目名称:lucky player
项目的主要功能:本系统主要功能为构建了一个用户分享音乐的平台,普通用户不进行登录即可收听其他用户已经发布的专辑中的音乐。
作为博主则可以在该平台上传音频,以及在线音频录制上传。音频上传成功后,博主可以把自己的音频整理到一个专辑内进行发布,并实现了在线播放的功能。该系统登录后的创作中心分为用户管理、音频管理、专辑管理三个模块。
二、项目需求
2.1功能需求
(1)用户可以注册后登录进播放器,并且也可以随时退出已经登陆的账户。
(2)用户可以自己录制音频进行上传,也可以从本地进行上传,并对上传的音乐进行管理。
(3)用户可以新建专辑将自己的音频进行收录,并且能够对专辑进行上线和下线的管理。
2.2 其他需求
(1)系统界面有良好的视觉体验,营造美观舒适的界面;
(2)操作简单流畅,无可视卡顿;
(3)有良好的引导提示,增强用户体验;
2.3 播放器功能流程图
2.4 总体设计
本系统采用了浏览器/服务器模式,即B/S模式。对表现层、业务层、持久层三层结构均进行了实现。
表现层(data_view):在表现层通过前端界面处理(html+css+JavaScript)配合前端框架进行实现。前端与用户直接接触,保证良好的设计风格和视觉体验。前端数据通过javaScript发送Ajax传输给后端,再通过后端servlet返回的数据进行DOM树的渲染,形成了最终的页面。
业务层(service包和servlet包):service对从数据库或者前端页面获取来的数据进行转换,转换为当下需要的数据格式。在业务层通过Servlet处理,进行前后端交互。由于前端数据需要向后端发出请求。所以在前后端交互处理使用了JavaScript的开源框架jQuery-Ajax进行数据请求响应处理。后端通过servlet接收对应数据进行处理。
持久层(util包、data_object、repository):通过JDBC对数据库进行了连接,创建了用户表、音频表、专辑表、以及关系表,用来存储信息,并创建建了四个表在后端的实体类(UserDo,TrackDo,AlbumDo,TidToCountDo),以及在view_object包下面定义我们需要的json格式的数据,以及对repository对数据库中数据的增删查改。
三、开发环境
1.前端开发:
技术:Html、Css、JavaScript
工具:Intellij IDEA 2020.1.4
2.后端开发:
算法:哈希算法进行加密
技术:jdk1.8、workbench、servlet、Maven
服务器:tomcat-8.5.50
工具:Intellij IDEA 2020.1.4
3.开发环境:Windows11 家庭版
4.运行环境:Intellij IDEA 2020.1.4
四、准备工作
1.创建 Spring Boot 项目
具体创建方法参考怎样用IDEA社区版以及企业版创建spring boot项目?这篇博客哟,注意在创建时记得勾选下面两个依赖
2.配置pom.xml内容(添加依赖)
通过<packaging>war</packaging>为后续打包,打成war包。通过第三方仓库导入MYSQL,Servlet,Thymeleaf,jackson的依赖。通过<build><finalName>${project.artifactld}</finalName></build>将war包名称改变,方便后续部署到云服务器。
3.配置MYSQL连接
在application.yml中配置关联数据库的相关信息
五、包的命名规则
data_object:用来存放与数据库直接交互的实体类
repository: 用来直接对数据库中的数据进行操作
service(服务层):把数据转换为当前需要的格式,当数据来自多张表需要在代码中做组装时,在Service中进行。
controller:进行前后端的交互,接收请求和发送响应给浏览器
session_object:定义浏览器需要的JSON格式的属性
resources:存储前端文档以及动态的资源,实现了页面的动态呈现。
六、各个功能的详细介绍
6.1库表的建立
建表语句
-- 修改 MySQL 服务器的查询包最大限制为 500M -- 但每次重启 MySQL 之后(包括重启电脑/关机之后)都需要手动再执行下 -- 直接去 MySQL Workbench 上去执行即可 set global max_allowed_packet = 500 * 1024 * 1024; -- 设置之后,需要将 MySQL Workbench 重新打开下 -- 设置之后,需要重启 Tomcat,让 MySQL 重新连接 create database lucky_player charset utf8mb4;use lucky_player;create table users (uid int primary key auto_increment,username varchar(20) not null unique,password char(60) not null );create table tracks (tid int primary key auto_increment,uid int not null,title varchar(10) not null,type char(40) not null,content longblob not null comment '音频的二进制数据' );create table albums (aid int primary key auto_increment,uid int not null,title varchar(10) not null,cover varchar(600) not null,state int not null comment '0: 已下线 / 1: 未发布 / 2: 已发布' );create table relations (rid int primary key auto_increment,aid int not null,tid int not null ) comment '维护专辑和音频之间的多对多关系';数据库中的表信息与data_object包对应,在后端操作的实际上是这里定义的数据库属性。
下面是对各表的详细介绍:
用户表
users:
音频表
tracks:
专辑表
albums:
关系表
relations:

relations表用于维护专辑与音频之间多对多的关系
数据库中的四个表对应data_object中的四个实体类
6.2用户管理
注册功能:
通过from表单发送HTTP的post请求,后端RegisterDoServlet接收HTTP请求,并进行相关的处理,在这个类里可以进行合法性校验,注册之后,将用户对象放入session中,再重定向到首页,重定向之后注册完成。
登录用到的类的介绍:
UsersSO: 是对外表现的对象,存放在session中,传给前端,只定义了uid 和username ,并没有把password写进这个类里面。
UserService: 完成注册(完成数据库地插入操作),在类中把UserDO(数据库需要的形式)转化为UserSO(我们需要的形式)。
UserDO:这里的数据是被数据库操作的,所以为了方便操作,属性名称都与数据库相同。
UserRepo: 进行sql操作,对User表操作。为了代码简洁,直接用@SneakyThrows (lombok包下),不添加throws也可以正常抛出受查异常。
为了是代码简洁,引入了 lombok.Data,@Data可以给我们自动添加getter/setter/toString/equals。
登录功能:
在LoginDoServlet中判断session
UserService:(3个操作)
(1)首先根据用户名在数据库中查出数据
(2)然后检查密码是否正确
(3)UserRepo用来进行查询操作
注销功能:
实现:把session中的currentUser删掉即可,在servlet中删除session
6.3.音频管理
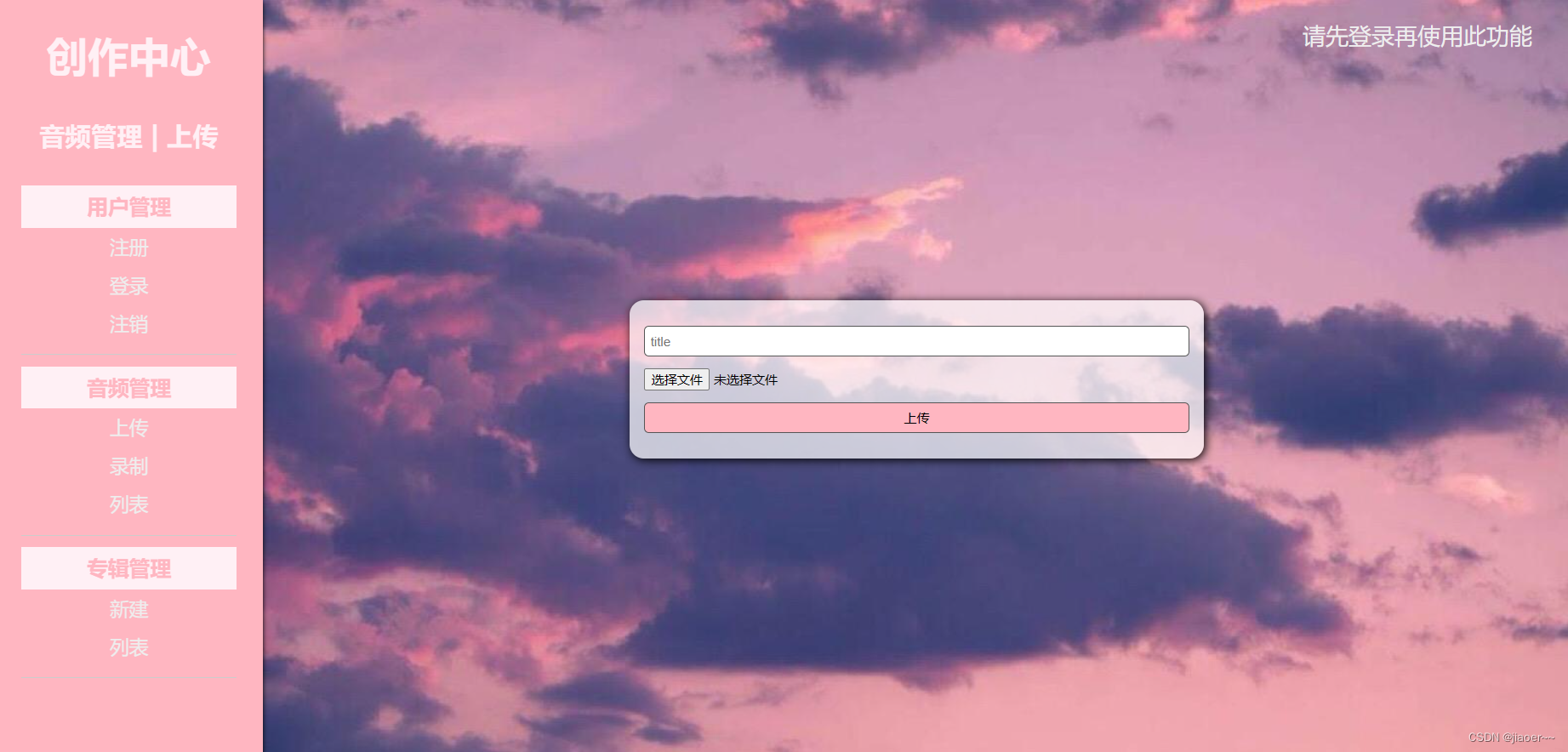
文件上传:
需要上传文件:前端 upload.html
(1)from必须使用post提交
(2)From的enctype必须是multipart/formdata
(3)input type=file
UploadDoServle类:用来接收前端的from表单,而要想接收enctype=multipart/formdata 必须使用@MultipartConfig修饰。
(1)首先第一步利用session来判断用户是否登录。
(2)从请求中获取我们需要的信息,我们要取title 、type(文件类型)、content(音频数据)
(3)将拿到的数据插入到数据库中,由于插入比较简单没有引入service,直接在UploadDoServle类中进行插入
Trackrepo类:对数据库进行操作的插入操作。
遇到的问题:由于mysql服务器支持的查询包的大小是4194304,但是上传的音频文件过大就无法上传。所以要进行mysql的设置,只要在workbench中执行SQL:
set global_allowed_packet=500*1024*1024;但每次重启MySQL都需要手动执行一下,即可。
音频列表:
1.采用前后端分离的技术:后端以json格式来提供数据
2.前端:通过Ajax(XHR技术),进行请求+进行DOM树的修改
3.指定具体的JSON格式
具体实现:
(1)前端list.html页面首先要加载JS,准备好展示的列表的容器元素(table/div),list.js发送ajax请求后端的JSON数据,js获取到数据之后进行DOM树的渲染
(2)在后端ListJsonServlet接收到js发送的HTTP请求构造响应,首先判断用户是否登录。
这是在StudioTrackListView中定义的两个属性 List<ListTrackView> trackList,currentUser赋值,如果未登录,则赋值为null即可,如果已登录则这个新的对象赋值为trackService(主要工作是把查询到的数据库TrackDo类型的数据转为ListTrackView类型的数据)中加工后的List集合。
在ListJsonServlet中把list集合的数据序列化为JSON格式的数据,传给前端js,浏览器解析js得到页面。
音频录制:
在前端record.html中留下容器<audio disabled controls></audio>用来开启浏览器的麦克风权限,然后再js中进行DOM树的渲染,给每一个前端的按钮都加上响应,让音频开始录制,结束录制,并且发送post请求,发送给RecordJsonServlet,由这个类把数据保存在数据库表中
6.4.专辑管理
新建专辑:
1.在前端create.html中用from表单提交前端传入的数据,后端用CreateDoServlet接收HTTP请求,接收到之后首先判断用户是否登录,若登录,直接把数据插入在数据库中,并返回专辑创建成功。(业务简单并没有用到service层辅助操作)
关联音频:
在bind.html中保存一个添加的a标签,点击之后,js再次发送HTTP请求,跳转到add.html(新增音频),然后add.js发送ajax请求,请求后端json格式的数据,后端把数据返回给前端,然后js进行渲染,把所有的音频呈现出来(复选框的形式)。
后端json格式的数据由CandidateJsonServlet来做,同样是判断用户是否登录,然后在数据库中查询数据,并把数据转化为JSON格式。
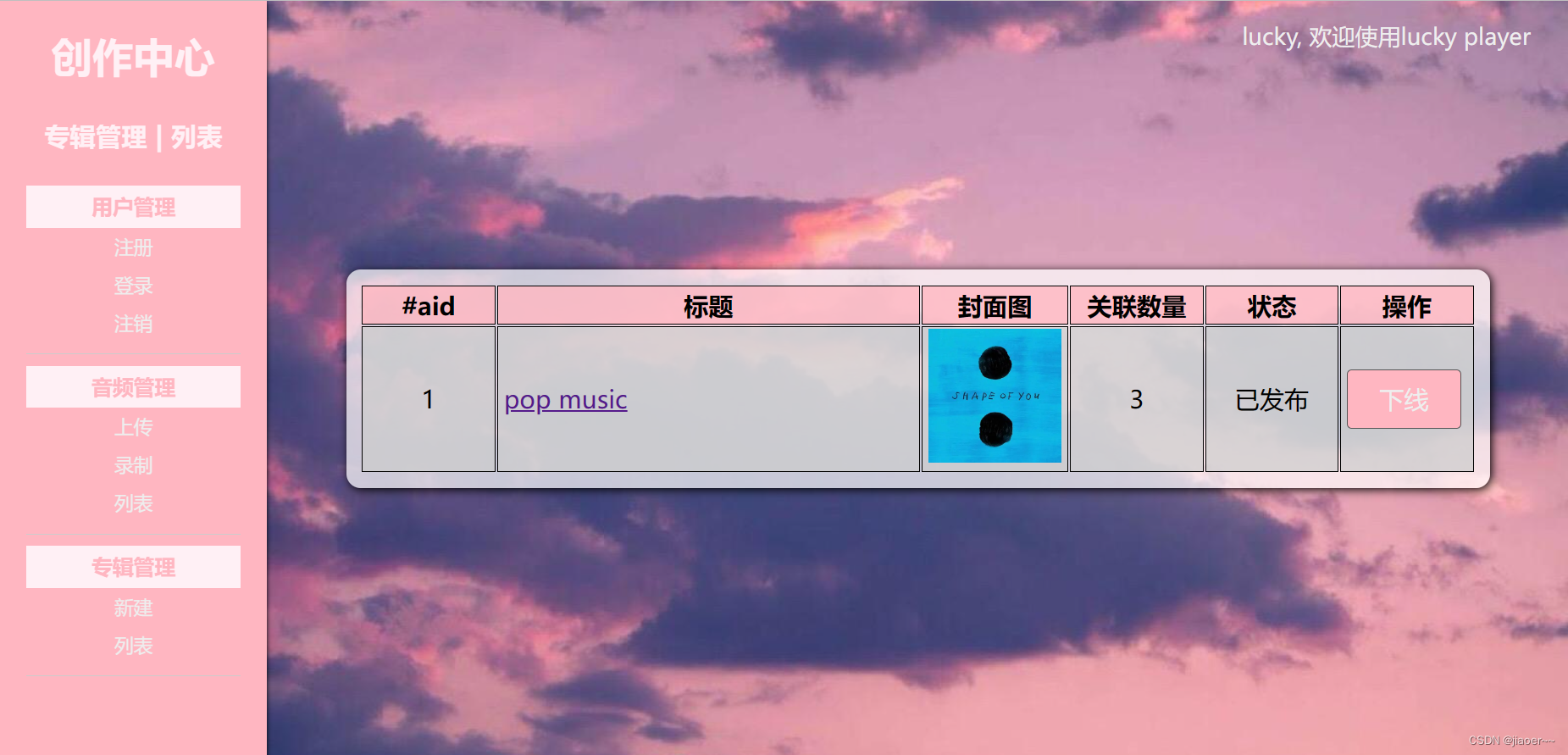
专辑列表:
同上面几乎相同,前端list.html中留下容器,经过js发送ajax得到数据对页面进行渲染得到,后端ListJsonServlet中创建了外部需要的类AblumView,并且写上构造方法,也创造了一个ResultView类定义了当前用户、和专辑列表,然后把数据库中查询得到的数据放在ablumList中,再把数据转化为JSON格式传给前端。