网站建设风险管理计划网上能注册公司吗怎么注册
初识Docker
1.什么是Docker
微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。
-
分布式系统中,依赖的组件非常多,不同组件之间部署时往往会产生一些冲突。
-
在数百上千台服务中重复部署,环境不一定一致,会遇到各种问题
1.1.应用部署的环境问题
大型项目组件较多,运行环境也较为复杂,部署时会碰到一些问题:
-
依赖关系复杂,容易出现兼容性问题
-
开发、测试、生产环境有差异

例如一个项目中,部署时需要依赖于node.js、Redis、RabbitMQ、MySQL等,这些服务部署时所需要的函数库、依赖项各不相同,甚至会有冲突。给部署带来了极大的困难。
1.2.Docker解决依赖兼容问题
而Docker确巧妙的解决了这些问题,Docker是如何实现的呢?
Docker为了解决依赖的兼容问题的,采用了两个手段:
-
将应用的Libs(函数库)、Deps(依赖)、配置与应用一起打包
-
将每个应用放到一个隔离容器去运行,避免互相干扰

这样打包好的应用包中,既包含应用本身,也保护应用所需要的Libs、Deps,无需再操作系统上安装这些,自然就不存在不同应用之间的兼容问题了。
虽然解决了不同应用的兼容问题,但是开发、测试等环境会存在差异,操作系统版本也会有差异,怎么解决这些问题呢?
1.3.Docker解决操作系统环境差异
要解决不同操作系统环境差异问题,必须先了解操作系统结构。以一个Ubuntu操作系统为例,结构如下:

结构包括:
-
计算机硬件:例如CPU、内存、磁盘等
-
系统内核:所有Linux发行版的内核都是Linux,例如CentOS、Ubuntu、Fedora等。内核可以与计算机硬件交互,对外提供内核指令,用于操作计算机硬件。
-
系统应用:操作系统本身提供的应用、函数库。这些函数库是对内核指令的封装,使用更加方便。
应用于计算机交互的流程如下:
1)应用调用操作系统应用(函数库),实现各种功能
2)系统函数库是对内核指令集的封装,会调用内核指令
3)内核指令操作计算机硬件
Ubuntu和CentOS都是基于Linux内核,无非是系统应用不同,提供的函数库有差异:

此时,如果将一个Ubuntu版本的MySQL应用安装到CentOS系统,MySQL在调用Ubuntu函数库时,会发现找不到或者不匹配,就会报错了:

Docker如何解决不同系统环境的问题?
-
Docker将用户程序与所需要调用的系统(比如Ubuntu)函数库一起打包
-
Docker运行到不同操作系统时,直接基于打包的函数库,借助于操作系统的Linux内核来运行
如图:

1.4.小结
Docker如何解决大型项目依赖关系复杂,不同组件依赖的兼容性问题?
-
Docker允许开发中将应用、依赖、函数库、配置一起打包,形成可移植镜像
-
Docker应用运行在容器中,使用沙箱机制,相互隔离
Docker如何解决开发、测试、生产环境有差异的问题?
-
Docker镜像中包含完整运行环境,包括系统函数库,仅依赖系统的Linux内核,因此可以在任意Linux操作系统上运行
Docker是一个快速交付应用、运行应用的技术,具备下列优势:
-
可以将程序及其依赖、运行环境一起打包为一个镜像,可以迁移到任意Linux操作系统
-
运行时利用沙箱机制形成隔离容器,各个应用互不干扰
-
启动、移除都可以通过一行命令完成,方便快捷
2.Docker和虚拟机的区别
Docker可以让一个应用在任何操作系统中非常方便的运行。而以前我们接触的虚拟机,也能在一个操作系统中,运行另外一个操作系统,保护系统中的任何应用。
两者有什么差异呢?
虚拟机(virtual machine)是在操作系统中模拟硬件设备,然后运行另一个操作系统,比如在 Windows 系统里面运行 Ubuntu 系统,这样就可以运行任意的Ubuntu应用了。
Docker仅仅是封装函数库,并没有模拟完整的操作系统,如图:

对比来看:

小结:
Docker和虚拟机的差异:
-
docker是一个系统进程;虚拟机是在操作系统中的操作系统
-
docker体积小、启动速度快、性能好;虚拟机体积大、启动速度慢、性能一般
3.Docker架构
3.1.镜像和容器
Docker中有几个重要的概念:
镜像(Image):Docker将应用程序及其所需的依赖、函数库、环境、配置等文件打包在一起,称为镜像。
容器(Container):镜像中的应用程序运行后形成的进程就是容器,只是Docker会给容器进程做隔离,对外不可见。
一切应用最终都是代码组成,都是硬盘中的一个个的字节形成的文件。只有运行时,才会加载到内存,形成进程。
而镜像,就是把一个应用在硬盘上的文件、及其运行环境、部分系统函数库文件一起打包形成的文件包。这个文件包是只读的。
容器呢,就是将这些文件中编写的程序、函数加载到内存中允许,形成进程,只不过要隔离起来。因此一个镜像可以启动多次,形成多个容器进程。

例如你下载了一个QQ,如果我们将QQ在磁盘上的运行文件及其运行的操作系统依赖打包,形成QQ镜像。然后你可以启动多次,双开、甚至三开QQ,跟多个妹子聊天。
3.2.DockerHub
开源应用程序非常多,打包这些应用往往是重复的劳动。为了避免这些重复劳动,人们就会将自己打包的应用镜像,例如Redis、MySQL镜像放到网络上,共享使用,就像GitHub的代码共享一样。
-
DockerHub:DockerHub是一个官方的Docker镜像的托管平台。这样的平台称为Docker Registry。
-
国内也有类似于DockerHub 的公开服务,比如 网易云镜像服务、阿里云镜像库等。
我们一方面可以将自己的镜像共享到DockerHub,另一方面也可以从DockerHub拉取镜像:

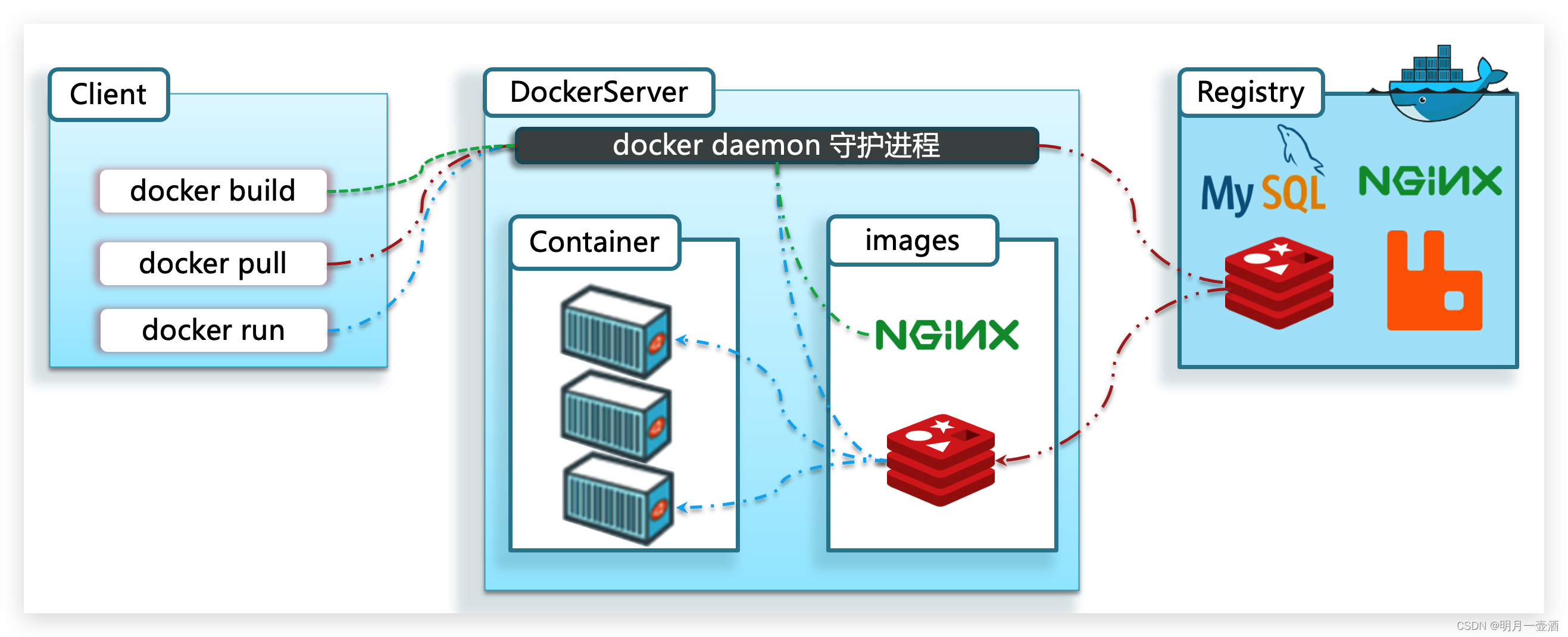
3.3.Docker架构
我们要使用Docker来操作镜像、容器,就必须要安装Docker。
Docker是一个CS架构的程序,由两部分组成:
-
服务端(server):Docker守护进程,负责处理Docker指令,管理镜像、容器等
-
客户端(client):通过命令或RestAPI向Docker服务端发送指令。可以在本地或远程向服务端发送指令。
如图:
3.4.小结
镜像:
-
将应用程序及其依赖、环境、配置打包在一起
容器:
-
镜像运行起来就是容器,一个镜像可以运行多个容器
Docker结构:
-
服务端:接收命令或远程请求,操作镜像或容器
-
客户端:发送命令或者请求到Docker服务端
DockerHub:
-
一个镜像托管的服务器,类似的还有阿里云镜像服务,统称为DockerRegistry
4.安装Docker
企业部署一般都是采用Linux操作系统,而其中又数CentOS发行版占比最多,因此我们在CentOS下安装Docker。参考文文章:
Docker安装
