北京网站建设怎么样烟台市建设工程质量监督站网站
每一步向前都是向自己的梦想更近一步,坚持不懈,勇往直前!
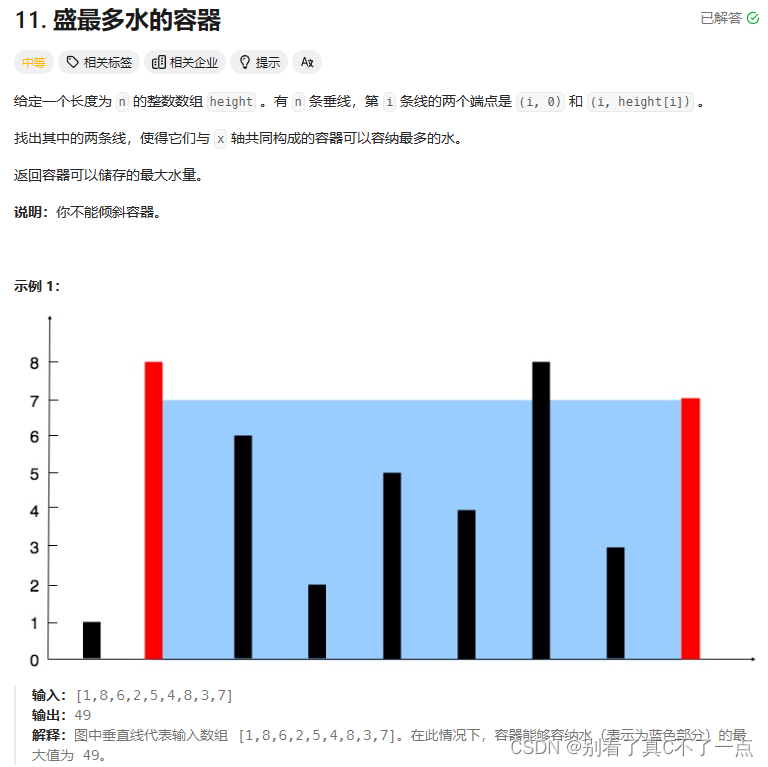
第一题:11. 盛最多水的容器 - 力扣(LeetCode)
class Solution {public int maxArea(int[] height) {//这道题比较特殊,因为两边是任意选的,//所以中间可以出现比两边高的情况,实际就是双指针求一个矩形的面积//宽度为左右边界的差值,高度为左右高度的较小值,所以我们进行模拟int l = 0, r = height.length - 1, maxres = 0;while(l < r){if(maxres < (r - l) * Math.min(height[l], height[r])){maxres = (r - l) * Math.min(height[l], height[r]);}//不断挪动边界,因为宽度是在不断缩小的,那么如果我们挪动较高的那边,//得到的结果一定比以前小,所以挪动较低的那一边if(height[l] <= height[r]){l++;}else{r--;}}return maxres;}
}第二题:12. 整数转罗马数字 - 力扣(LeetCode)


class Solution {// 数值对应的罗马数字int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};// 罗马数字String[] symbols = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};// 将整数转换为罗马数字public String intToRoman(int num) {StringBuilder sb = new StringBuilder();// 遍历数值对应的数组for (int i = 0; i < values.length; ++i) {int value = values[i];String symbol = symbols[i];// 当 num 大于等于当前数值时,循环减去该数值,并将对应的罗马数字追加到结果中while (num >= value) {num -= value;sb.append(symbol);}// 如果 num 等于 0,表示已经转换完成,直接跳出循环if (num == 0) {break;}}// 返回转换后的罗马数字字符串return sb.toString();}
}
第三题:13. 罗马数字转整数 - 力扣(LeetCode)


class Solution {// 将罗马数字转换为整数public int romanToInt(String s) {int res = 0; // 结果变量,用于存储转换后的整数值int preNum = getValue(s.charAt(0)); // 前一个罗马数字对应的整数值// 遍历字符串 s 中的每个字符for(int i = 1; i < s.length(); i++){int num = getValue(s.charAt(i)); // 当前字符对应的整数值// 如果前一个字符对应的整数值小于当前字符对应的整数值,则将结果减去前一个字符对应的整数值if(preNum < num){res -= preNum;}else{ // 否则,将结果加上前一个字符对应的整数值res += preNum;}preNum = num; // 更新前一个字符对应的整数值为当前字符对应的整数值}res += preNum; // 加上最后一个字符对应的整数值return res; // 返回最终的整数值}// 获取字符对应的整数值private int getValue(char ch){switch(ch) {case 'I' : return 1;case 'V' : return 5;case 'X': return 10;case 'L': return 50;case 'C': return 100;case 'D': return 500;case 'M': return 1000;default: return 0;}}
}
第四题:14. 最长公共前缀 - 力扣(LeetCode)

import java.util.Arrays;
import java.util.Comparator;class Solution {// 寻找字符串数组中的最长公共前缀public String longestCommonPrefix(String[] strs) {// 根据字符串长度对数组进行排序Arrays.sort(strs, new Comparator<String>(){@Overridepublic int compare(String o1, String o2){return o1.length() - o2.length();}});// 获取最短字符串的长度int maxlen = strs[0].length();int res = 0, index = 0; // res: 公共前缀长度,index: 当前比较的字符索引// 遍历最短字符串的长度while(index < maxlen){char tmpch = '.'; // 临时变量,用于存储当前比较的字符,默认为'.'表示未初始化// 遍历字符串数组中的每个字符串for(String st : strs){// 如果临时字符是'.',则将当前字符作为临时字符if(tmpch == '.'){tmpch = st.charAt(index);}// 否则,如果当前字符与临时字符不相等,则返回公共前缀(如果 res 不为 0),否则返回空字符串else{if(st.charAt(index) != tmpch){return res != 0 ? strs[0].substring(0, res) : "";}}}index++; // 移动到下一个字符位置res++; // 更新公共前缀长度}// 返回最长公共前缀return strs[0].substring(0, res);}
}
第五题:15. 三数之和 - 力扣(LeetCode)

class Solution {// 定义一个方法threeSum,接收一个整数数组nums作为参数,返回所有和为0的三元组public List<List<Integer>> threeSum(int[] nums) {// 初始化结果列表List<List<Integer>> res = new ArrayList<>();// 对数组进行排序,以便于后续的双指针操作Arrays.sort(nums);// 遍历数组,使用i作为第一个数字for(int i = 0; i < nums.length - 2; i++) {// 跳过相同的元素,避免重复的三元组if(i > 0 && nums[i] == nums[i - 1]) {continue;}// 初始化左右指针int j = i + 1, k = nums.length - 1;// 使用while循环进行双指针操作,寻找和为0的三元组while(j < k) {// 计算当前三元组的和int cursum = nums[i] + nums[j] + nums[k];// 如果当前和小于0,说明需要增大和,因此移动左指针jif(cursum < 0) {j++;} else if(cursum > 0) {// 如果当前和大于0,说明需要减小和,因此移动右指针kk--;} else {// 如果当前和为0,找到了一个三元组res.add(Arrays.asList(nums[i], nums[j], nums[k]));// 跳过相同的元素,避免重复的三元组while(j < k && nums[j] == nums[j + 1]) {j++;}while(j < k && nums[k] == nums[k - 1]) {k--;}// 移动指针继续寻找下一个可能的三元组j++;k--;}}}// 返回所有找到的三元组return res;}
}