网页排版精美的中文网站设计手机网站
典型相关分析概述:研究两组变量(每组变量都可能有多个指标)之间的相关关系的一种多元统计方法,能够揭示两组变量之间的内在联系。
典型相关分析的思想:把多个变量和多个变量之间的相关化为两个具有代表性的变量之间的相关性。对于一组变量来说,最简单的代表即原始变量的线性组合。
典型相关分析的步骤:
①在每组变量中找出变量的线性组合,使得两组线性组合之间具有最大的相关系数;
②选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选择相关系数最大的一对;
③重复上述步骤,直到两组变量之间的相关性被完全提取完毕。
被选出的线性组合配对称为典型变量,它们的相关系数被称为典型相关系数。典型相关系数衡量了两组变量之间的联系强度。
使用SPSS进行典型相关分析:
- 导入数据后依次点击:
分析→相关→典型相关性
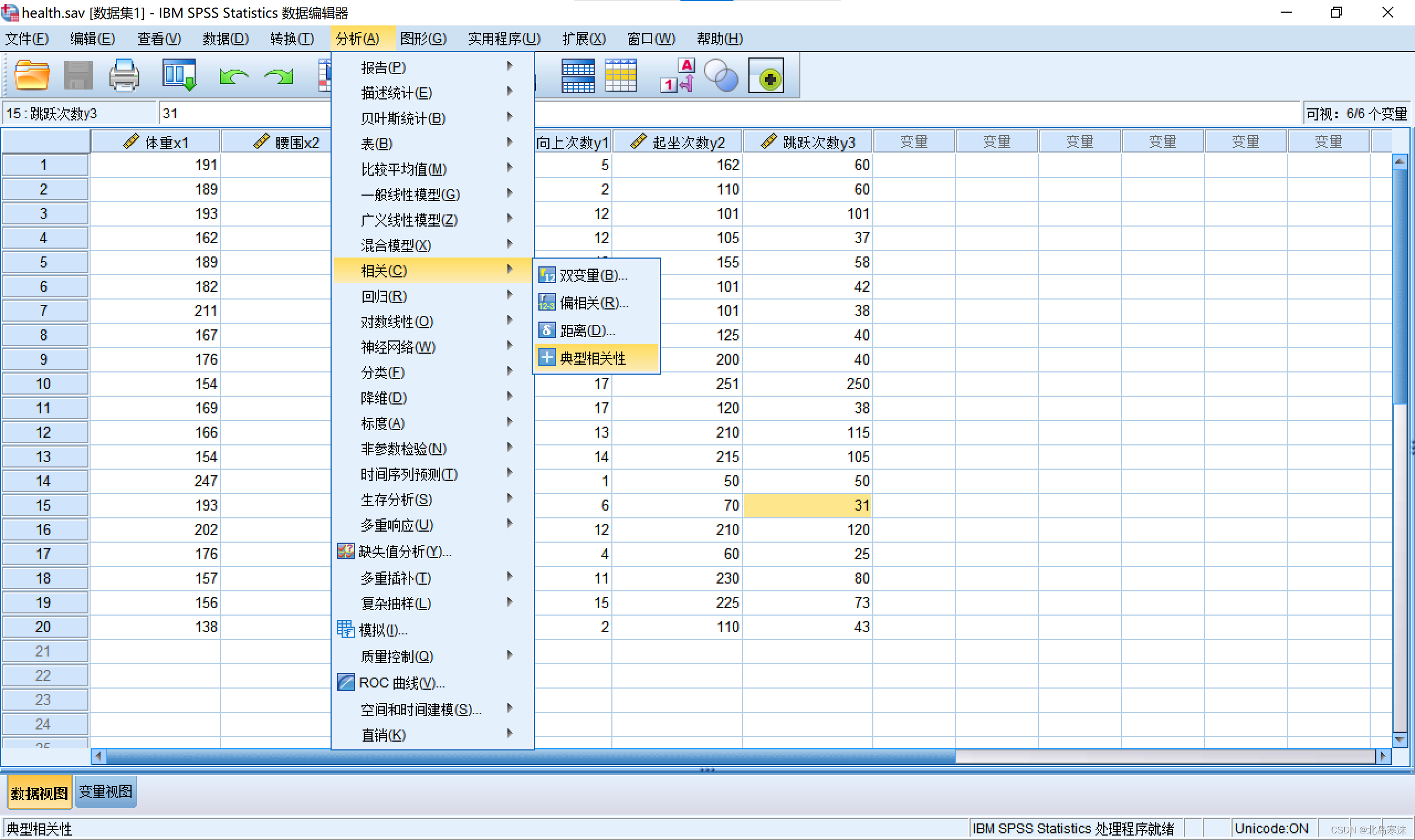
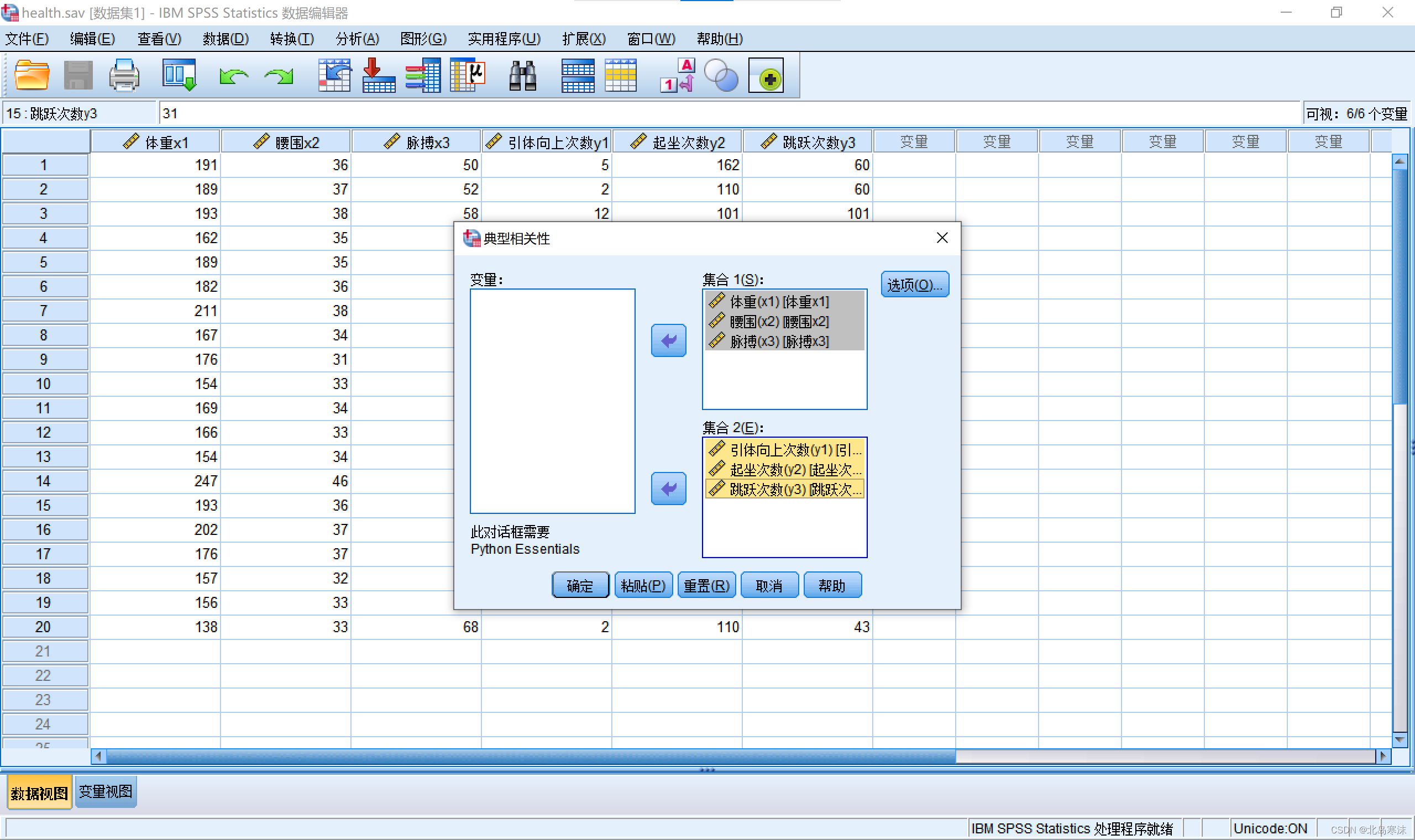
- 依次把两组变量的指标放入两个集合中
典型相关分析结果解读:
- 典型相关系数表:表格的第一列给出了相关系数,最后一列给出了相关系数对应的P值(用于进行显著性检验)。
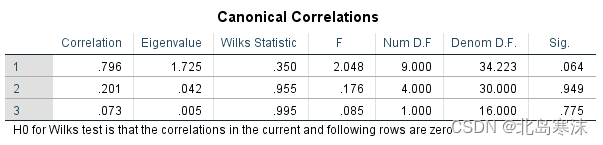
上表中,第一对典型相关变量的相关系数为0.796,当显著性水平为0.1的情况下,其P值小于显著性水平,因此可以认为两个变量之间存在相关性,且相关性显著。 - 典型相关变量对应的组合系数表:
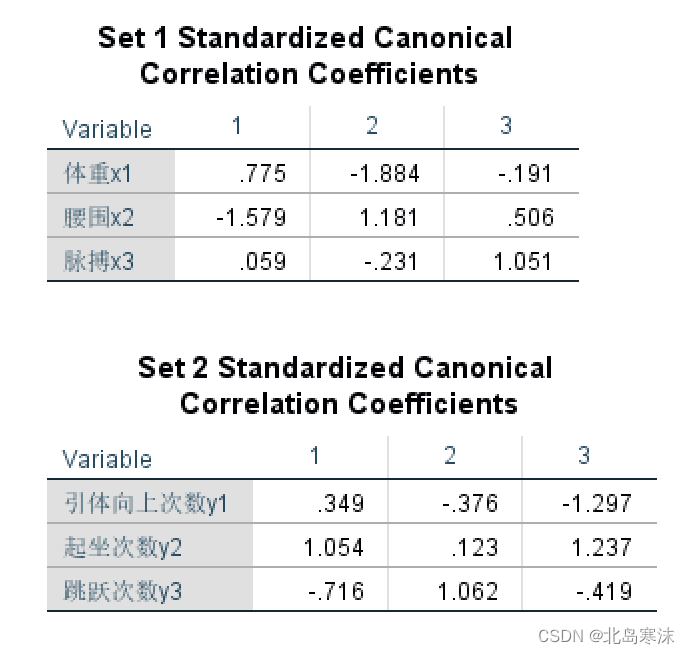
需要提前进行标准化:典型相关分析涉及多个变量,不同的变量往往有不同的量纲和数量级。在进行典型相关分析时,由于典型变量是原始变量的线性组合,具有不同量纲变量的线性组合显然失去了实际意义。齐次,不同数量级的变量也会导致分析结果的合理性。因此,需要对数据进行标准化处理后再进行典型相关分析。
需要进行载荷分析:可以通过标准化后的典型相关分析,找出典型相关变量和哪些指标的关系大,以及与指标的关系正负如何。
