wordpress制作网站模板十堰网站seo方法
Git基础入门
Git是一个分布式 版本管理系统,用于跟踪文件的变化和协同开发。
版本管理:理解成档案馆,记录开发阶段各个版本
分布式&集中式
分布式每个人都有一个档案馆,集中式只有一个档案馆。分布式每人可以管理自己的档案馆,当自己觉得代码完成,可以提交自己的档案馆与他人的进行合并
github、gitlab、gitee都是基于git工具做的托管平台。
1.安装与配置
1.1 下载与安装
下载网址:https://git-scm.com/download/
安装
window可以默认安装
linux:sudo apt-get install git
Microsoft提供的安装教程
1.2配置
打开终端window需要右键打开git bush输入命令
MAC和linux可以通过终端直接输入命令
$ git config --global user.name “你的昵称”
$ git config --global user.email 邮箱@example.com
注:配置只是说明性的,做一个标记并不等于之后的注册与登陆。
1.3 GUI
常用git gui可以见git官网
推荐:[Gitkraken]、[SourceTree]、[TortoiseGit]
2. git命令
2.1 命令总览
git bush输入命令行git
start a working area (see also: git help tutorial)clone Clone a repository into a new directoryinit Create an empty Git repository or reinitialize an existing onework on the current change (see also: git help everyday)add Add file contents to the indexmv Move or rename a file, a directory, or a symlinkrestore Restore working tree filesrm Remove files from the working tree and from the indexsparse-checkout Initialize and modify the sparse-checkoutexamine the history and state (see also: git help revisions)bisect Use binary search to find the commit that introduced a bugdiff Show changes between commits, commit and working tree, etcgrep Print lines matching a patternlog Show commit logsshow Show various types of objectsstatus Show the working tree statusgrow, mark and tweak your common historybranch List, create, or delete branchescommit Record changes to the repositorymerge Join two or more development histories togetherrebase Reapply commits on top of another base tipreset Reset current HEAD to the specified stateswitch Switch branchestag Create, list, delete or verify a tag object signed with GPGcollaborate (see also: git help workflows)fetch Download objects and refs from another repositorypull Fetch from and integrate with another repository or a local branchpush Update remote refs along with associated objects2.2常用命令
2.2.1 帮助命令
| 命令 | 作用 |
|---|---|
| git help [command] | 帮助命令 |
2.2.2 创建仓库
| 命令 | 作用 |
|---|---|
| git init | 创建⼀个git本地仓库,⽣成⼀个.git⽬录,其他⽬录不变 |
| git clone | 拷⻉⼀份远程仓库(类似 svn checkout) |
2.2.3 修改和提交
| 命令 | 作用 |
|---|---|
| git status | 查看本地仓库当前的状态,显⽰有变更的⽂件 |
| git add | 添加⽂件到本地仓库 |
| git commit | 提交暂存区到本地仓库 |
| git rm | 删除⼯作区⽂件 |
| git mv | 移动或重命名⼯作区⽂件 |
| git diff | ⽐较⽂件的不同 |
| git reset | 回退版本 |
2.2.4 提交日志
| 命令 | 作用 |
|---|---|
| git log | 查看历史提交记录 |
| git reflog | 看所有分⽀的所有操作记录(包括提交、回退、已删除的提交操作记录等) |
2.2.5 分支管理
| 命令 | 作用 |
|---|---|
| git checkout | 切换或者新建分⽀ |
| git merge | 合并分⽀ |
| git rebase | 变基 |
| git branch | 分支管理 |
2.2.6 远程管理
| 命令 | 作用 |
|---|---|
| git remote | 远程仓库操作 |
| git fetch | 从远程获取代码库 |
| git pull | 下载远程代码并合并 |
| git push | 上传远程代码并合并 |
2.2.7 标签
| 命令 | 作用 |
|---|---|
| git tag | 管理标签 |
3.文件与提交
3.1 git原理
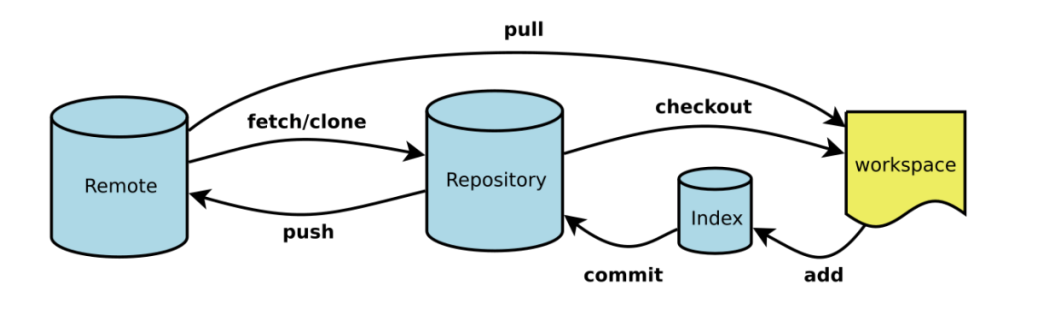
Workspace:⼯作区,就是在电脑能看到的⽬录
Index / Stage:暂存区,存放在.git⽬录下的index⽂件中
Repository:仓库区(或本地仓库),⼯作区有⼀个隐藏⽬录 .git,这个不算⼯作区,⽽是 Git 的版本库
Remote:远程仓库,著名的如github和gitee
3.2本地仓库
新建git仓库时文件处于未跟踪状态(clone的代码仓库里文件处于未修改状态),可以通过git add .将文件夹下所有文件添加至暂存区,再通过git commit -m "this is first submit"(“引号内可自定义”)提交至仓库区,此时文件处于已追踪未修改的的状态。后续修改文件都会被git追踪,修改完成后重复git add和git commit。

3.2 撤销提交
git reset head~ --soft命令,但是无法撤销第一次提交
git reset三个参数--soft --mix hard的区别
| 工作区 | 暂存区 | |
|---|---|---|
| –soft | 保留 | 保留 |
| –mix | 保留 | 丢弃 |
| –hard | 丢弃 | 丢弃 |
查看暂存区文件指令git ls_files
3.3远程仓库
3.3.1 添加远程仓库
git remote add origin https://xxxxxxxx
推送本地代码git push origin master
3.3.2 SSH
github ssh配置参考
在实际开发过程中会因为开发新功能、修复bug或者多人协同开发需要创建分支。
4.分支
4.1 branch
git branch创建分支,但是没有切换分支
git switch切换分支,在git -v2.23版本后支持。之前版本可以使用git checkout命令切换分支,在分支名和文件名一样时git checkout存在歧义,会默认切换分支。
4.2 merge
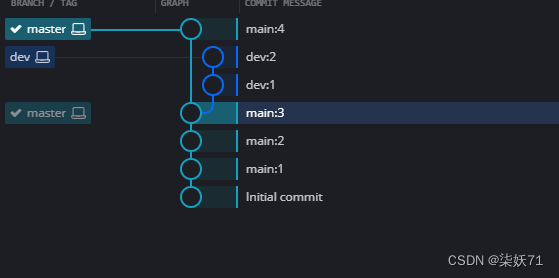
git merge xxx将xxx分支内容的更改合并到当前分支上。
例如创建两个分支,master分支存main.txt,dev分支存dev.txt文件,当我们需要将dev分支合并到master分支时,需要确保当前分支是master分支可以使用git switch master切换当前分支,执行git merge dev将dev分支上内容合并到主分支上,如下图所示:
`
4.3 rebase
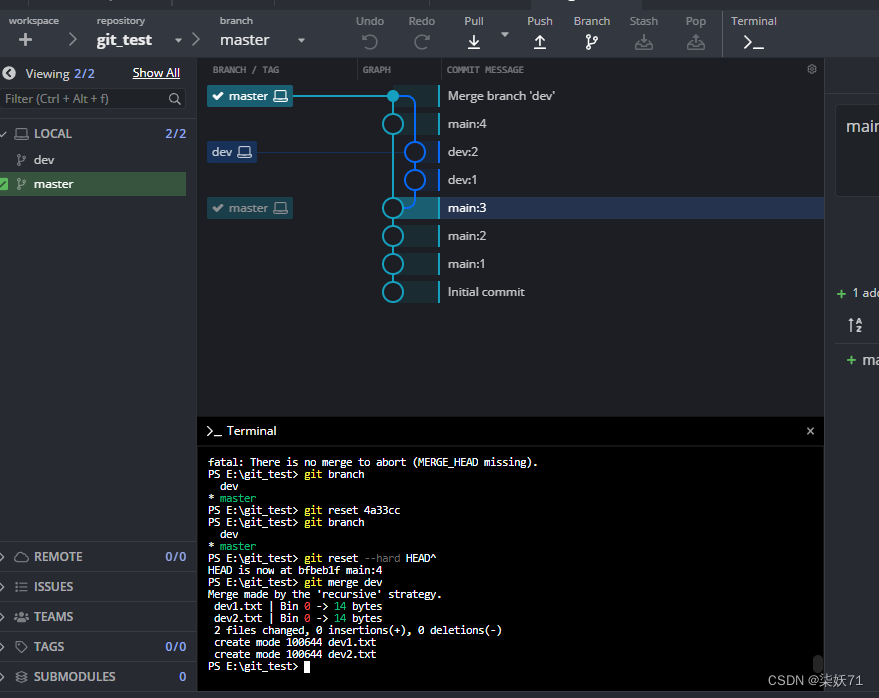
git rebase xxx将xxx分支内容的更改变基到当前分支上。以下图分支说明

变基指令会先寻找分支的祖先节点,例程中是main:3节点,若当前分支是master分支,执行git rebase dev则会将当前分支的mian:4 节点移到dev分支的后面,如下图所示:
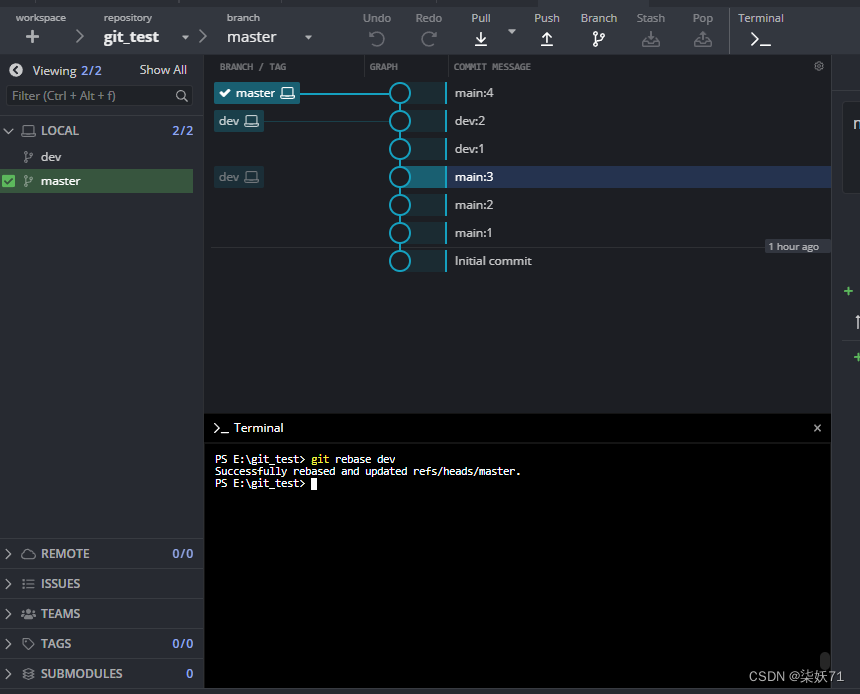
若当前分支是dev分支,执行git rebase master则会将当前分支的dev:1 dev:2 节点移到master分支的后面,如下图所示。
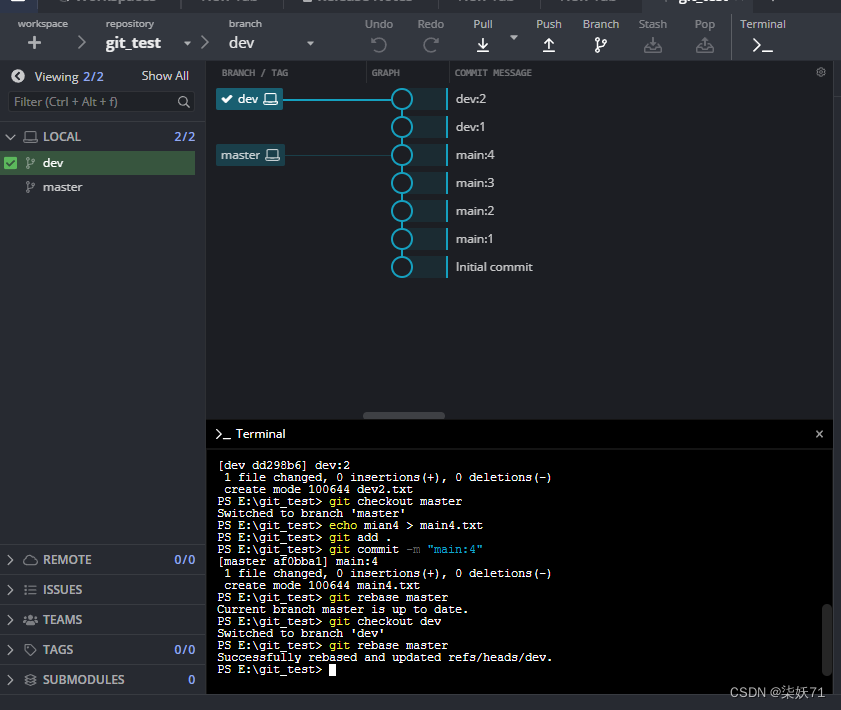
rebase会导致篡改历史,图4.3为例dev:1的基变成了main:4。在rebase前图4.1所示,dev:1的基是main:3。
4.3 merge VS rebase
| merge | rebase | |
|---|---|---|
| 优点 | 不会破坏历史,方便回溯与查看 | 不新增提交记录,形成线性历史 |
| 缺点 | 会产生额外提交节点,分支图复杂 | 会改变提交历史,改变branch out节点 |
4.3分支冲突
当两个分支进行不兼容操作时则会产生分支冲突。例如:若master分支和feat分支都对同一个文件的同一行进行修改。
step1:先新建一个feat分支然后修改main1.txt的内容,如图所示:(图片后续切回去截的)
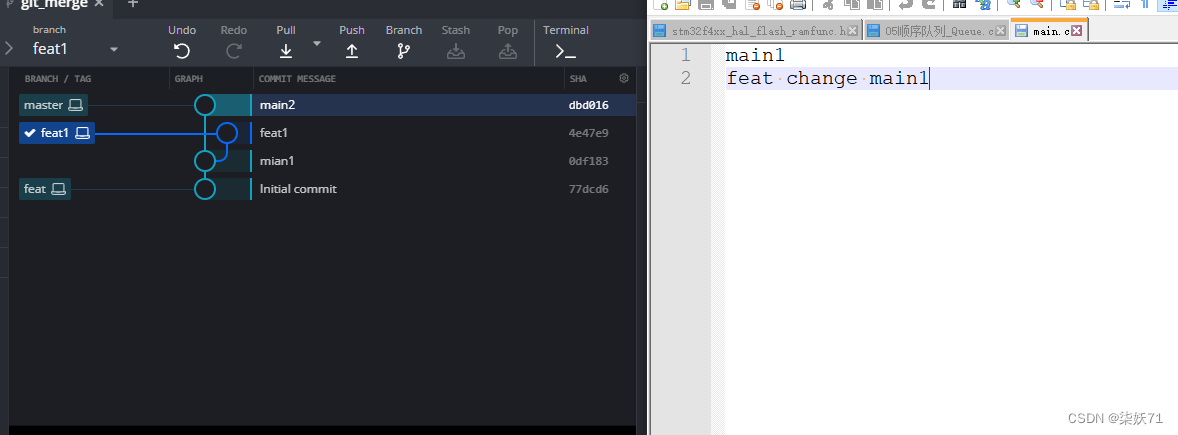
step2:然后切回master分支,刚刚的修改内容消失,因为切回master最后状态,修改同一行内容,然后提交,结果如图。
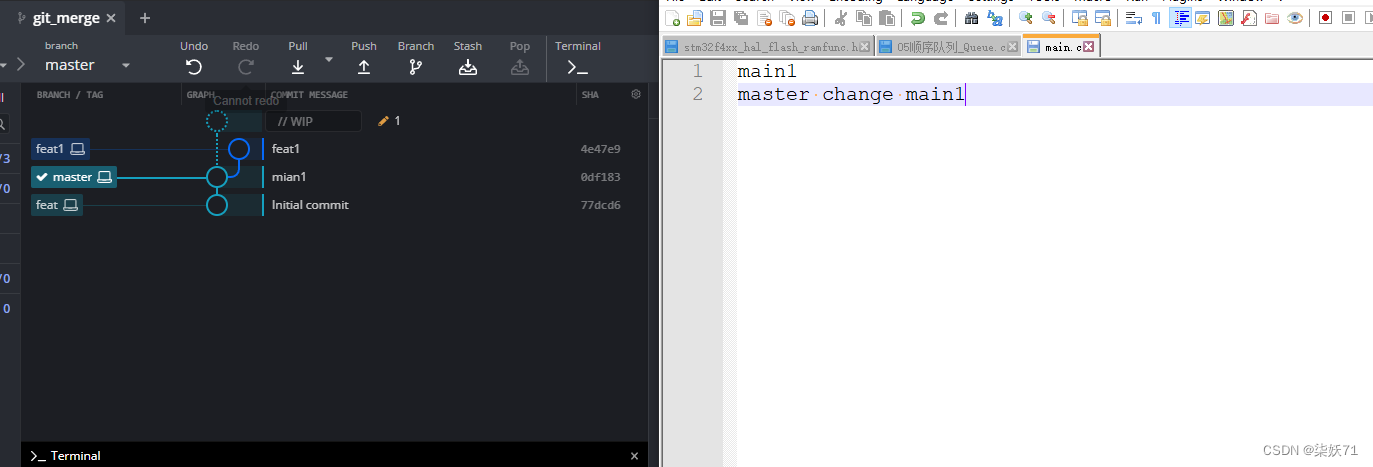
step3:当我们执行代码合并时则会显示分支冲突
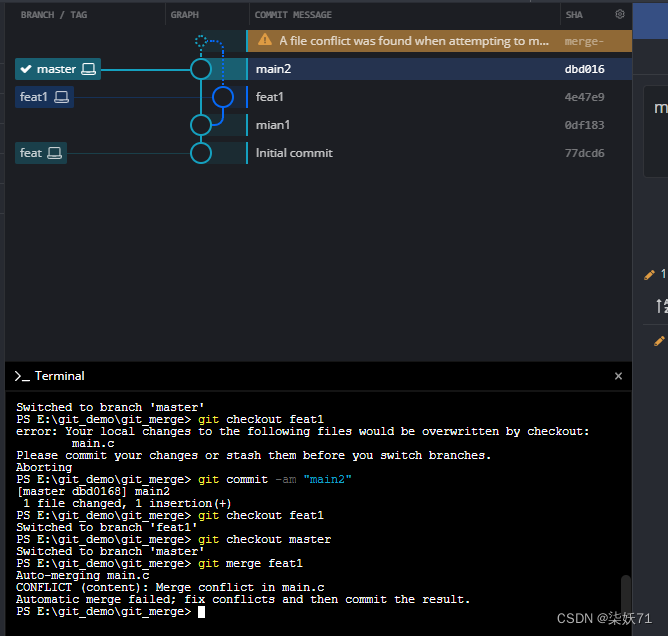
step4:使用git diff命令查看具体冲突。👉图也显示文件中显示了具体冲突。

step 5:删除<<<<<<< ======= >>>>>>> feat1,修改冲突

step 6:再执行git add . 和git commit命令完成分支合并
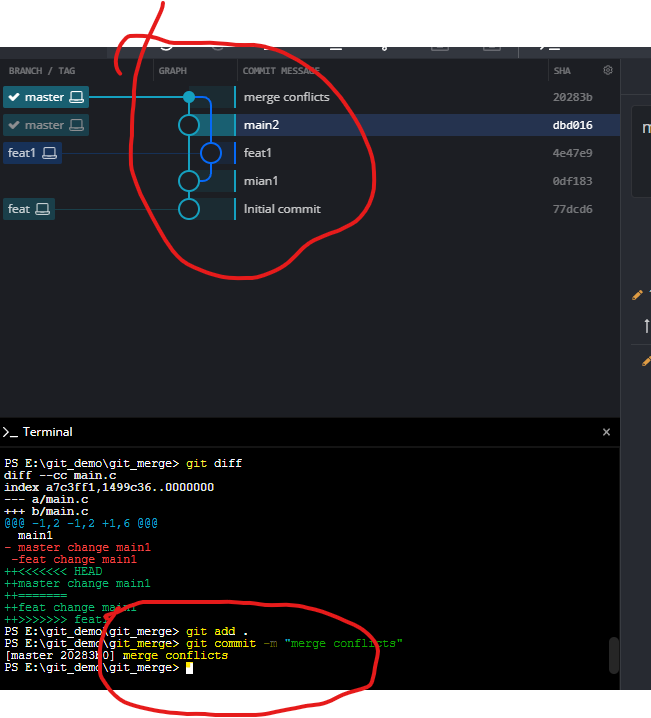
总结:手动解决分支冲突:使用git diff命令查找冲突文件,选择保留原有或者变更代码。修改后执行git add保存变更文件,再执行git merge或者git rebase --continue操作继续合并代码。
借助第三方工具提供UI界面:
可以二选一或者两个都选择。
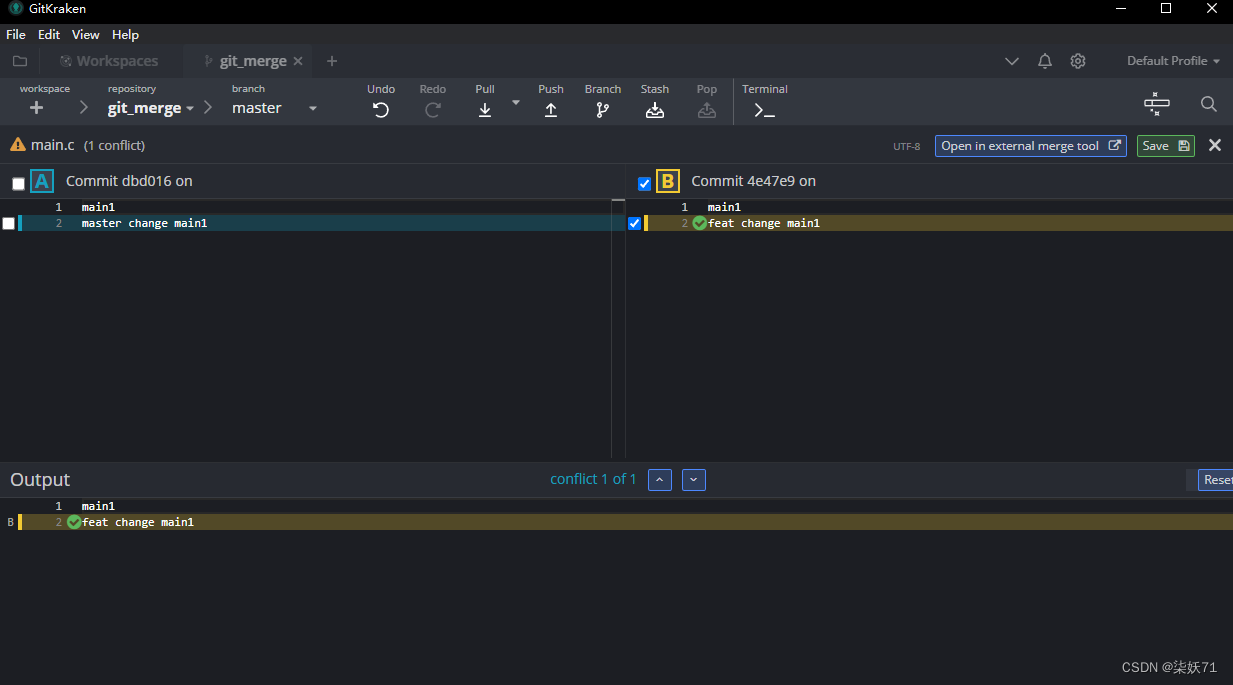
然后写入commit点击提交按钮即可,这比手动修改便捷一些。
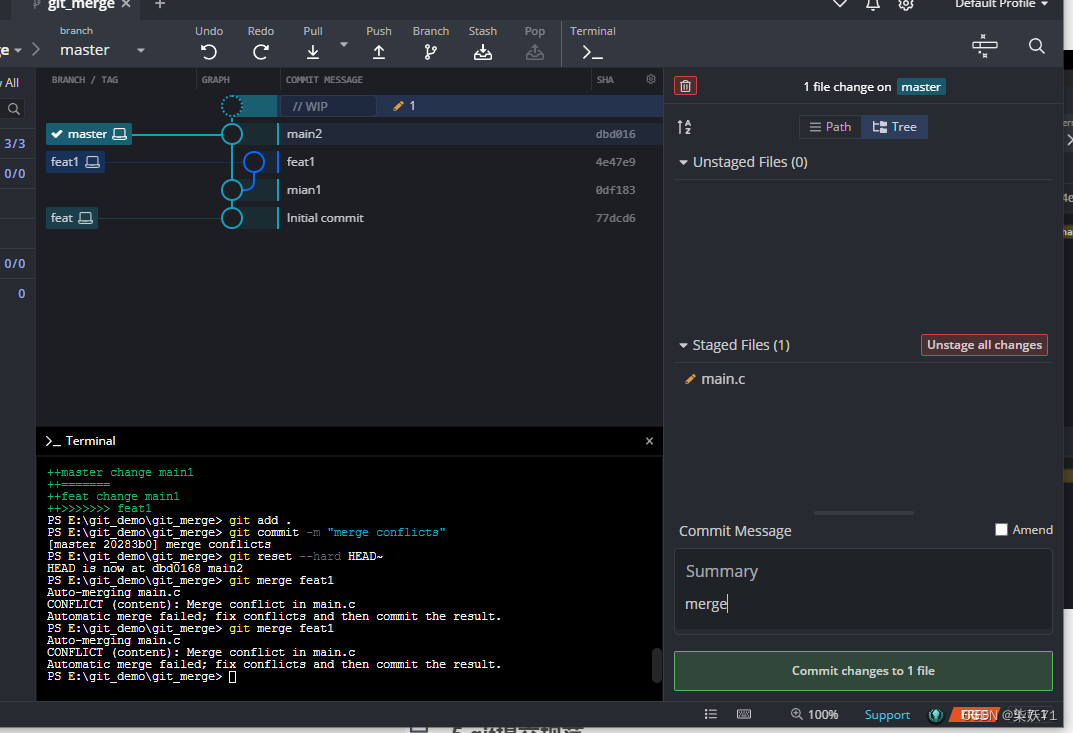
终止合并或者变基:
执行git merge --abort或者git rebase --abort取消合并。
5.git提交规范
常见的提交规范叫做"Conventional Commits"
消息结构:
每个提交消息包含一个简短的提交类型(type),可选的作用域(scope)以及详细的提交描述(description)。
各部分之间用冒号(:)分隔,细节描述与前面的部分用空格分隔。
例如:feat(user): add login functionality
提交类型(type):
feat: 新功能(feature)
fix: 修复问题(bug fix)
docs: 文档更新
style: 代码风格调整,不涉及功能性变动
refactor: 重构代码
test: 添加或修改测试代码
chore: 其他不涉及代码修改的任务
作用域(scope)(可选):
表示变更的范围或影响的组件/模块。可以是文件路径、模块名、功能域等。
提交描述(description):
提供详细的提交说明,描述变更的具体内容。
示例:
feat(user): add login functionality- Added login form and validation
- Implemented authentication API integration
- Updated user profile page5.1工作流: gitflow模型

master:可直接发布生产的分支。只接受hotfix和release的请求合并,不允许直接修改。(主要分支)
hot fixes:解决线上问题,修复后合并回main分支。命名规则 hotfix-#issueid-desc。
release:版本发布分支,永久分支用于发布前测试和验证。
develop:开发分支。(主要分支)
feature:功能分支,从开发分支分离开发新功能。命名规则:feature-pdbus-function
适用与开发水平适中有一定开发流程和规范的团队。
5.2 工作流:github flow模型
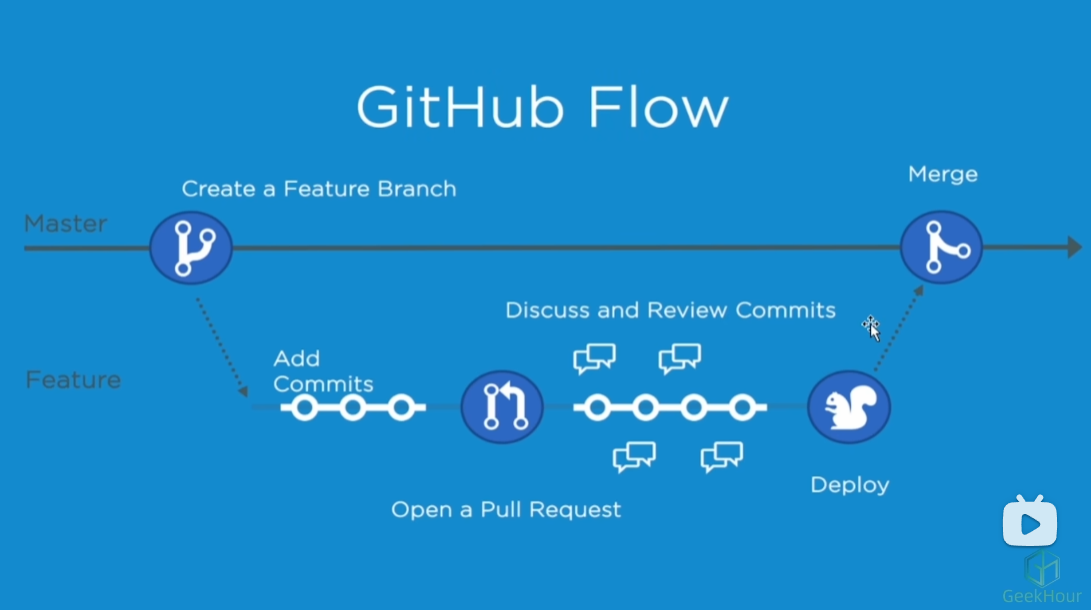
master:长期存在的主分支,主分支上代码可以直接发布生产,禁止团队成员直接在主分支上提交
featurn:团队成员在feature上开发,结束后提交合并,由代码功能评审团队评审后合并到master分支。
参考
GeekHour
30分钟弄懂所有工作Git必备操作 / Git 入门教程
附录1:GIT与SVN
来源chatgpt
Git和SVN是两种常用的版本控制系统,用于管理项目的源代码和跟踪文件的变化。下面是Git和SVN之间的一些区别:
分布式 vs 集中式:Git是一种分布式版本控制系统,每个开发者都可以拥有完整的代码仓库副本,并且可以在不联网的情况下进行提交和查看历史记录。SVN是一种集中式版本控制系统,所有代码都存储在中央仓库中,开发者需要联网才能进行提交和查看历史记录。
分支和合并:Git具有强大的分支和合并功能,可以轻松创建和管理多个分支,用于同时进行多个功能的开发或修复。Git的分支操作非常快速和轻量级。SVN也支持分支和合并,但相对复杂和耗时。
历史记录:Git的历史记录是基于文件内容的快照,每次提交都会创建一个新的快照。SVN的历史记录是基于文件的差异,每次提交都会记录文件变化的差异。因此,在Git中查看历史记录更快。
版本号:Git使用SHA-1哈希作为版本号,确保每个版本都具有唯一的标识符。SVN使用递增的版本号,例如1、2、3等。
分布式开发:由于Git是分布式的,开发者可以在本地进行提交和分支操作,而不受中央服务器的限制。这在团队分散和无网络连接的情况下非常有用。SVN在没有网络连接时,无法进行提交和分支操作。
冲突解决:Git具有更强大的冲突解决功能,开发者可以手动解决冲突并进行提交。SVN的冲突解决相对较弱,较常见的情况是手动编辑冲突文件并使用特定命令解决。
需要注意的是,Git和SVN适用于不同的项目和团队,选择哪种版本控制系统取决于具体需求和团队偏好。 Git更适合分布式开发、速度快、分支管理灵活等场景,而SVN适合集中式开发、简单易用等场景。
