五屏网站建设品牌好昆山专业网站建设
在数字化时代,我们的工作和生活都围绕着海量的数据和文件展开。然而,随着数据量的不断增加,如何高效地管理这些数字资产成为了摆在我们面前的一大难题。今天,我要向您介绍一种革命性的方法——利用办公软件实现文件夹编号批量复制与移动,让您轻松掌握数字世界的控制权。
第一步,如何根据文件夹编号把整个文件夹都复制或移动到指定的文件夹中呢?如“新建文件归类”这个表格所示:
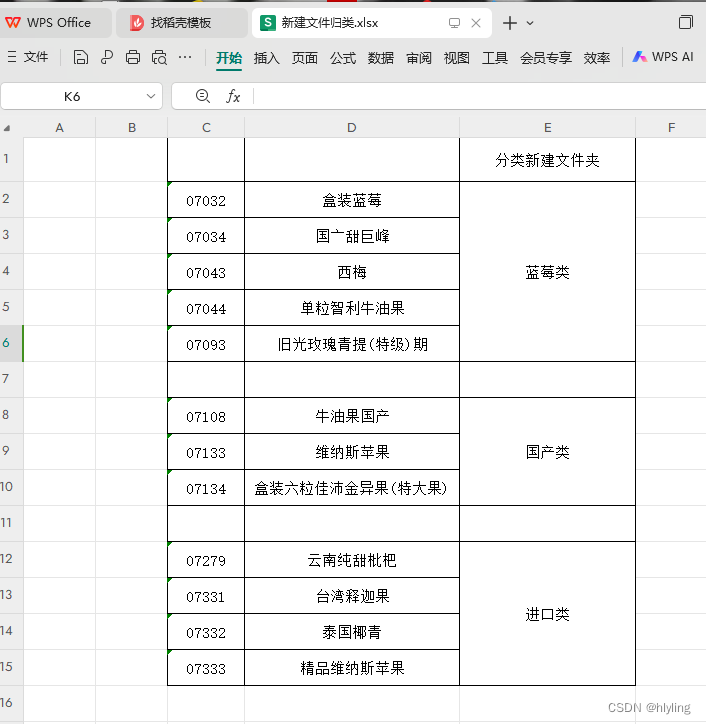
第二步,打开广佛水果文件夹,可以看到文件夹中有多个带有编号和名称的文件夹,而每个文件夹中又有多个子文件夹和文件

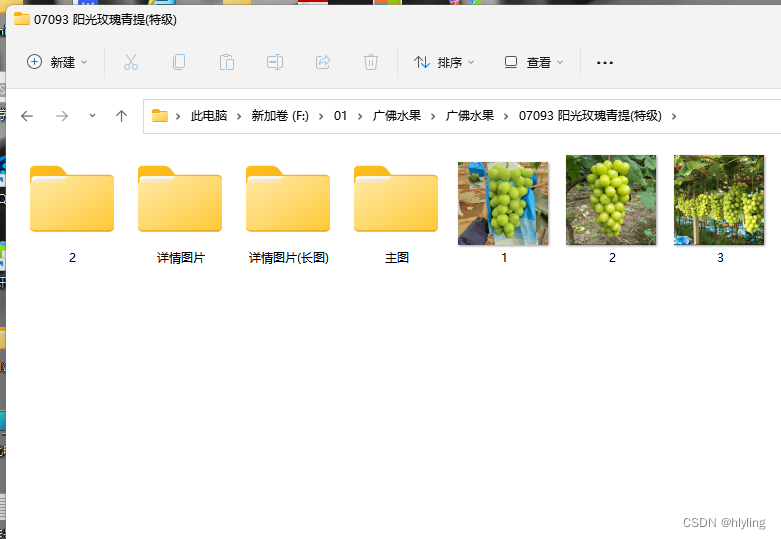
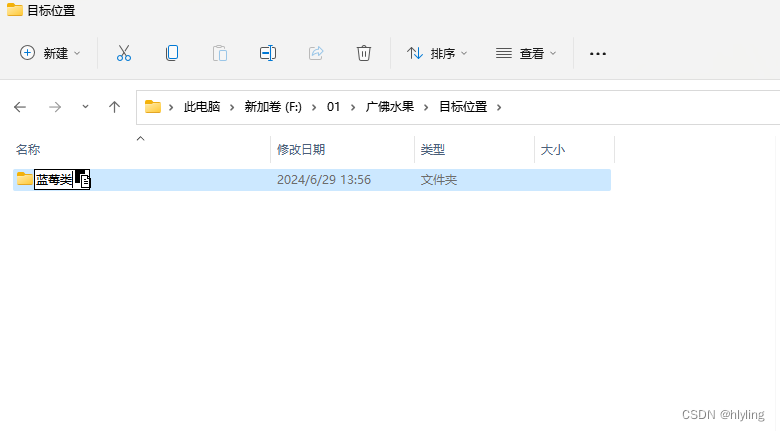
第三步,在文件夹相同的位置那里建立一个新文件夹并重命名为目标位置

第四步,打开“新建文件归类”表格,将“蓝莓类”进行选中,即E2-E6进行右击,并在下拉列表里选择复制即可。

第五步,在目标位置的文件夹里再次新建一个子文件夹,将复制好的内容进行粘贴进去,命名为“蓝莓类”
第六步,进入首助编辑高手的主页面,选择文件批量处理板块,并切换到“智能分发文件”功能,在点击添加文件夹,来进行操作。

第七步,在弹出来的窗口里,将广佛水果”这个主文件夹中的所有带编号的文件夹素材全选,在点击选择文件夹,进行导入到软件的源文件/文件夹里即可。

第八步,接着,将任务名称切换到“按关键词分发”和“目录”,在任务列表里,点击分组,将添加好的任务按分组一来进行分类,下拉分组列表选择分组一。
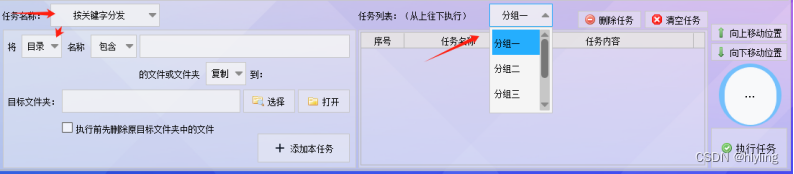
第九步,回到“新建文件归类”的表格里,复制c2这一栏单元格的数据,将其粘贴至软件中,并设置将目录名称包含07032的文件或文件夹复制或移动到到目标文件夹”

第十步,点击“选择”按钮,在弹出来的文件夹里选择目标位置里的蓝莓类为目标文件夹。

第十一步,设置好目标文件夹之后,点击添加本任务,将该任务一进行添加到右边任务列表里的分组一里面。

第十二步,如何快速生成多个根据文件夹编号复制或移动指定文件夹的分发任务呢?可以右击软件中,我们刚才新添加的任务一,选择下拉列表中的“复制任务”,很快提示复制任务成功

第十三步,然后将该任务粘贴到“新建文件归类”表格中的G2这一单元格中,任务数据如下图所示:按关键字分发<<d1kf>>将[{目录}]名称:[{包含}]关键字:[{07032}]的文件或文件夹复制到目标文件夹:[{F:\01\广佛水果\目标位置\蓝莓类\}],执行前不删除原目标文件夹中的文件
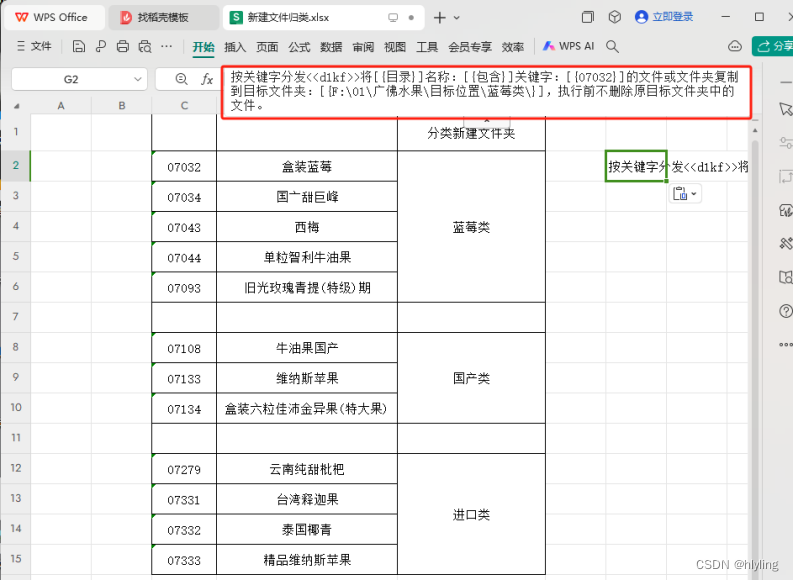
第十四步,选中蓝莓类这一列,再点击上方功能栏里的“合并”按钮,将该单元格与各自对应的行进行自动合并起来,接着,下拉光标放在蓝莓类单元格右下角并往下拉自动填充,将下方的单元格都显示为“蓝莓类”,而“国产类”和“进口类”的单元格合并和填充以此类推即可完成操作,并把表格中多余的两行进行删除

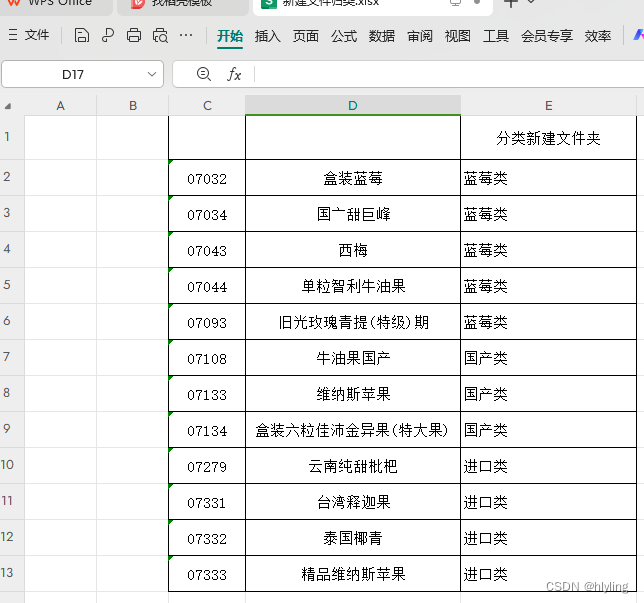
第十五步,接着在“G2”中调整一下任务数据,调整为:=“按关键字分发<<d1kf>>将[{目录}]名称:[{包含}]关键字:[{"&C2&"}]的文件或文件夹复制到目标文件夹:[{F:\01\广佛水果\目标位置\&E2&"\}],执行前不删除原目标文件夹中的文件。”

第十六步,设置完毕之后,将G2这一格下拉,自动填充到G13这个单元格里,就会一键生成多个根据不同文件夹编号分发文件夹的的分发任务
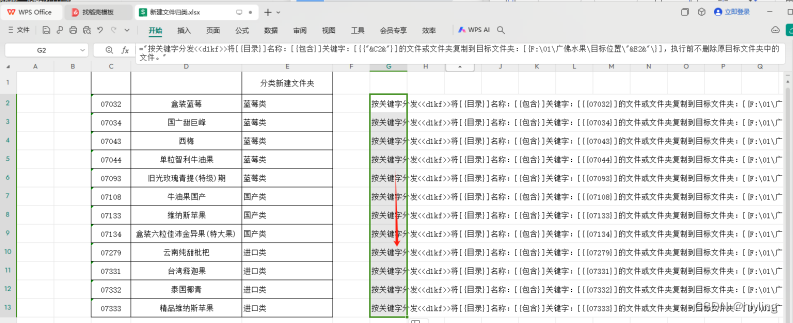
第十七步,选中G2到G13这些单元格,并右击,选择下拉列表中的复制功能,即可
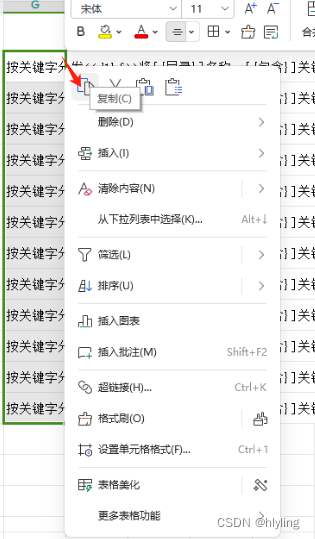
第十八步,回到主页面,清空任务列表里的任务,进行右击选择粘贴任务,将刚刚复制好的多个分发任务进行粘贴到任务列表里面。

第十九步,我们就可以点击执行任务,软件就会开始执行各个分发任务,操作速度很快

第二十步,执行完毕之后,打开目标位置文件夹进行查看,就会发现一组文件一个文件夹自动分类保存着,各个文件夹名称都是指定的
第二十一步,打开每个文件夹,就能发现每个文件夹里都分发了文件和子文件夹,说明已经成功文件夹编号把整个文件夹都复制或移动到指定的文件夹中

