定制旅游哪个网站好用青岛营销型网站推广
本地保存mysql凭据
- mysql加密登录文件简介
- 加密保存mysql用户的密码到本地凭据
mysql加密登录文件简介
要在 mysql客户端 上连接 MySQL 而无需在命令提示符上输入用户名和口令,下列三个位置可用于存储用户的mysql 凭证来满足此要求。
配置文件my.cnf或my.ini
/etc/my.cnf$MYSQL_HOME/my.cnf
这是MySQL的主要配置文件,可以包含数据库服务器和客户端的配置信息。在[client]部分可以配置连接信息,包括用户名和密码,但通常不推荐将明文密码直接写入配置文件中,因为这可能会带来安全风险。
加密登录文件 :
$HOME/.mylogin.cnf
该文件不能明文编辑
[client]
user = your_username
password = your_password
加密保存mysql用户的密码到本地凭据
使用mysql_config_editor工具来设置MySQL登录凭据。
# 创建一个默认的登录路径(login-path),并将其命名为“client”。
mysql_config_editor set --user=root --password

# 使用mysql_config_editor工具来设置一个名为“mysqldump”的特定登录路径。
# “mysqldump”路径通常用于mysqldump工具以便备份数据库。
mysql_config_editor set --login-path=mysqldump --user=root --password
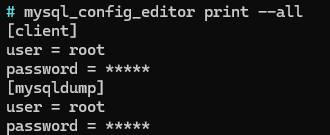
# 查看保存的mysql登录凭据
mysql_config_editor print --all

