tinypng图片压缩网站东莞房价2021最新价格走势
活跃主机发现技术指南
- 1.活跃主机发现技术简介
- 2.基于ARP协议的活跃主机发现技术
- 3.基于ICMP协议的活跃主机发现技术
- 4.基于TCP协议的活跃主机发现技术
- 5.基于UDP协议的活跃主机发现技术
- 6.基于SCTP协议的活跃主机发现技术
- 7.主机发现技术的分析
1.活跃主机发现技术简介
在生活中有这样一个默认的约定,当听到有人敲门的时候,屋子里的人会做出相应的回应,可能会询问,也可能会开门。有些时候一些居心不良的人就利用了这一点进行所谓的“踩点”
如果想知道网络中的某台主机是否处于活跃状态,同样可以采用这种“敲门”的方式,只不过需要使用发送数据包的形式来代替现实生活中的“敲门”动作,也就是说活跃主机发现技术其实就是向目标计算机发送数据包,如果对方主机收到了这些数据包,并给出了回应,就可以判断这台主机是活跃主机。
2.基于ARP协议的活跃主机发现技术
基于ARP协议的活跃主机发现技术的原理是:如果想要知道处在同一网段的IP地址为*.*.*.*的主机是否为活跃主机,只需要构造一个ARP请求数据包,并广播出去,如果得到了回应,则说明该主机为活跃主机
这种发现技术的优点在于准确度高,任何处于同一网段的设备都没有办法防御这种技术,因为如果不遵守ARP,那么将意味着无法通信。缺点在于这种发现技术不能对处于不同网段的目标主机进行扫描
使用Nmap的选项-PR就可以实现ARP协议的主机发现:
Nmap -sn -PR 192.168.1.1
结果:
Starting Nmap 7.12 ( https://Nmap.org ) at 2016-08-13 11:29
Nmap scan report for 192.168.0.1
Host is up (0.0030s latency). ①
MAC Address: D8:FE:E3:B3:87:A9 (D-Link International). ②
Nmap done: 1 IP address (1 host up) scanned in 1.82 seconds
上例中对IP地址为192.168.1.1的设备是否为活跃主机进行了检测,从结果中可以看到
- ①中的“
Host is up”这说明设备为活跃主机 - ②中给出了192.168.1.1设备的物理地址(
D8:FE:E3:B3:87:A9)
如果在发出了ARP请求数据包之后,却迟迟得不到ARP响应数据包的话,就可以认为该IP地址所在的设备不是活跃主机
3.基于ICMP协议的活跃主机发现技术
ICMP的报文可以分成两类:差错和查询
查询报文是用一对请求和应答定义的。也就是说,主机A为了获得一些信息,可以向主机B发送ICMP数据包,主机B在收到这个数据包之后,会给出应答。
ICMP中适合使用的查询报文包括如下3类:
1、响应请求和应答用来测试发送与接收两端链路及目标主机TCP/IP协议是否正常,只要收到就是正常。我们日常使用最多的是ping命令,利用响应请求和应答,主机A向一个主机B发送一个ICMP报文,如果途中没有异常(例如被路由器丢弃、目标不回应ICMP或传输失败),则主机B返回ICMP报文,说明主机B处于活跃主机
2、时间戳请求和应答ICMP时间戳请求允许系统向另一个系统查询当前的时间。返回的建议值是自午夜开始计算的毫秒数。如果想知道B主机是否在线,还可以向B主机发送一个ICMP时间戳请求,如果得到应答的话就可以视为B主机在线。当然,其实数据包内容并不重要,重要的是是否收到了回应。
3、地址掩码请求和应答ICMP地址掩码请求由源主机发送,用于无盘系统在引导过程中获取自己的子网掩码。
Nmap通过ICMP响应请求和应答进行主机发现
使用Nmap的选项-PE就可以实现ICMP协议的主机发现。这个过程实质上和ping是一样的
Nmap -sn -PE 60.2.22.35
通过ICMP时间戳请求和应答进行主机发现
使用Nmap的选项-PP就可以实现ICMP协议的时间戳主机发现
Nmap -sn -PP 60.2.22.35
通过ICMP地址掩码请求和应答进行主机发现
使用Nmap的选项-PM可以实现ICMP协议的地址掩码主机发现
nmap -PM 211.81.200.8
4.基于TCP协议的活跃主机发现技术
在Nmap中常用的TCP协议扫描方式有两种,分别是TCP SYN扫描和TCP ACK扫描,这两种扫描方式其实都是利用TCP的三次握手实现的。
TCP SYN扫描
目标主机在收到Nmap所发送的SYN数据包之后,会认为Nmap所在主机想要和自己的一个端口建立连接,如果这个端口是开放的,目标主机就会按照TCP三次握手的规定,发回一个SYN/ACK数据包,表示同意建立连接。如果这个端口是关闭的,目标主机就会拒绝这次连接,向Nmap所在主机发送一个RST数据包
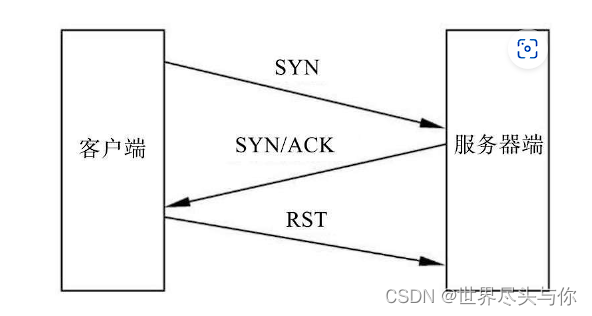
在发出SYN数据包之后,只要收到数据包,无论是SYN/ACK数据包还是RST数据包,都意味着目标主机是活跃的。如果没有收到任何数据包,就意味着目标主机不在线
在Nmap中可以使用-PS参数来实现这种扫描
Nmap -sn -PS 60.2.22.35
Nmap所在主机在收到这个数据包之后,并不会真的和目标主机建立连接,因为目的只是判断目标主机是否为活跃主机,因此需要结束这次连接,TCP协议中结束连接的方法就是向目标发送一个RST数据包
TCP ACK扫描
实际上它和SYN扫描相当相似,不同之处只在于Nmap发送的数据包中使用TCP/ACK标志位,而不是SYN标志位
Nmap直接向目标主机发送一个TCP/ACK数据包,目标主机显然无法清楚这是怎么回事,当然也不可能成功建立TCP连接,因此只能向Nmap所在主机发送一个RST标志位的数据包,表示无法建立这个TCP连接
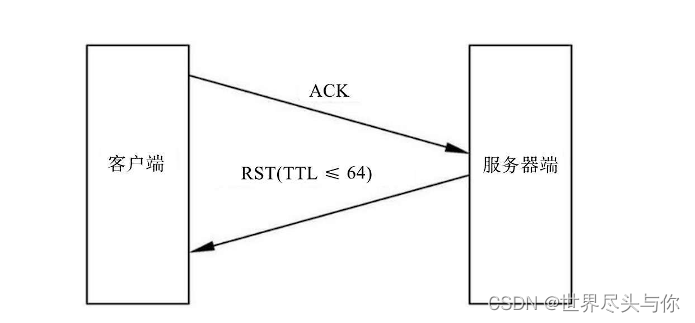
如果需要对目标主机采用这种扫描方式,可以使用如下命令
Nmap -sn -PA 60.2.22.35
在Nmap发出数据包之后,并没有收到任何应答,这时存在两种可能
- 一种是这个数据包被对方的安全机制过滤掉了,因为目标根本没有收到这个数据包
- 另一种就是目标主机并非活跃主机
Nmap通常会按照第二种情况进行判断,也就是给出一个错误的结论:目标并非活跃主机
5.基于UDP协议的活跃主机发现技术
当一个UDP端口收到一个UDP数据包时,如果它是关闭的,就会给源端发回一个ICMP端口不可达数据包;如果它是开放的,就会忽略这个数据包,也就是将它丢弃而不返回任何信息
这样做的优点就是可以完成对UDP端口的探测,而缺点为扫描结果的可靠性比较低。因为当发出一个UDP数据包而没有收到任何的应答时,有可能因为这个UDP端口是开放的,也有可能是因为这个数据包在传输过程中丢失了。另外,扫描的速度很慢。原因是在RFC1812中对ICMP错误报文的生成速度做出了限制。例如Linux就将ICMP报文的生成速度限制为每4秒产生80个,当超出这个限制的时候,还要暂停1/4秒
使用Nmap的选项-PU就可以实现UDP协议的主机发现
Nmap -sn -PU 60.2.22.35
TCP需要扫描目标主机开放的端口,而UDP需要扫描的是目标主机关闭的端口。在扫描的过程中,需要避开那些常用的UDP协议端口,例如DNS(端口53)、SNMP(161)。因此在扫描的时候,最合适的做法就是选择一个值比较大的端口,例如35462
6.基于SCTP协议的活跃主机发现技术
SCTP协议与TCP完成的任务是相同的。但两者之间却存在着很大的不同之处
- TCP协议一般是用于单地址连接的,而SCTP却可以用于多地址连接
- TCP协议是基于字节流的,SCTP是基于消息流的。TCP只能支持一个流,而SCTP连接同时可以支持多个流
- TCP连接的建立是通过三次握手实现的,而SCTP是通过一种4次握手的机制实现的,这种机制可以有效避免攻击的产生
在SCTP中,客户端使用一个INIT报文发起一个连接,服务器端使用一个INIT-ACK报文进行应答,其中就包括了cookie(标识这个连接的唯一上下文)。然后客户端使用一个COOKIE-ECHO报文进行响应,其中包含了服务器端所发送的cookie。服务器端要为这个连接分配资源,并通过向客户端发送一个COOKIE-ACK报文对其进行响应
使用Nmap的选项-PY就可以向目标主机发送一个SCTP INIT数据包
Nmap -sn -PY 60.2.22.35
7.主机发现技术的分析
Nmap中提供了--packet-trace选项,通过它就可以观察Nmap发出了哪些数据包,收到了哪些数据包,有了这个研究方法,可以更深入地理解Nmap的运行原理
Nmap在进行主机发现的时候,无论你指定了何种方式,Nmap都会先判断一下目标主机与自己是否在同一子网中,如果在同一子网中,Nmap直接使用ARP协议扫描的方式,而不会使用你所指定的方式。
