门户网站免费奖励自己北京网站建设 网站维护
目录
- 1、接口新特性
- 1.1 JDK8的新特性
- 1.2 JDK9的新特性
- 2、代码块
- 2.1 代码块的定义
- 2.2 代码块的分类
- 3、内部类
- 3.1 内部类的定义
- 3.2 内部类成员访问
- 3.3 学习内部类的原因
- 3.4 内部类的分类
- 3.4.1 成员内部类
- 3.4.2 静态内部类
- 3.4.3 局部内部类
- 3.4.4 匿名内部类
- (1)定义:
- (2)使用场景:
- 4、Lambda表达式
- 4.1 概述
- 4.2 案例
- 4.3 注意事项
- 4.4 Lambda表达式的省略写法
- 4.5 Lambda表达式和匿名内部类的区别
- 5、窗体、组件、事件
- 5.1 窗体
- 5.2 组件
- 5.2.1 按钮组件Jbutton
- 5.2.2 文本组件Jlabel
- 5.3 事件
- 5.4 适配器设计模式
- 5.5 模板设计模式
1、接口新特性
1.1 JDK8的新特性

之前说过,接口里面只能是抽象方法,但是JDK8为何要修改成允许定义带方法体的方法呢,原因是什么呢?
答:如果系统要升级版本2,那么在接口中再新加抽象方法时,会导致以前的接口实现对象报错,因此JDK8改成接口中可以定义有方法体的方法,就是为了解决:丰富接口功能的同时,又不需要更改实现类的代码。,如下图:
下面再看下JDK8是怎么做的:
1.2 JDK9的新特性

为什么JDK9允许定义私有方法呢?
答:
下面看看JDK9是如何做的:
2、代码块
2.1 代码块的定义

2.2 代码块的分类

package com.itheima.vo;public class Student {//随着类的加载而加载,多用于数据初始化static {System.out.println("Student类的静态代码块...");}//编译时,会分散到每个构造方法的第一行{System.out.println("Student类的构造代码块...");}public Student(){//现在电脑内存都很大了,所以一般不会使用局部代码块提前释放内存{System.out.println("局部代码块...");}System.out.println("Student类的构造方法...");}
}
注:同步代码块多线程会使用到,这个放多线程介绍。
3、内部类
3.1 内部类的定义

下面是一个例子:
package com.itheima.inner;public class InnerTest {public static void main(String[] args) {Outer.Inner in = new Outer().new Inner();//创建内部类对象in.show();//调用内部类方法}
}class Outer{class Inner{int num = 11;public void show(){System.out.println("show...");}}
}
3.2 内部类成员访问

看下面这三个变量,第一个是外部类成员变量、第二个是内部类成员变量、第三个是方法里的变量,现在的问题是,如何分别访问他们三个?
答:看代码
class Outer{int num = 11;//外部类成员变量class Inner{int num = 22;//内部类成员变量public void show(){int num = 33;//方法里的变量System.out.println(num); //33System.out.println(this.num); //22System.out.println(Outer.this.num); //11}}
}
注:
1、方法里的变量:直接访问,即就近原则;
2、内部类成员变量:使用this关键字;
3、外部类成员变量:使用外部类名称.this访问。
3.3 学习内部类的原因

3.4 内部类的分类

3.4.1 成员内部类
如下所示的Inner就是成员内部类:
class Outer{class Inner{int num = 11;public void show(){System.out.println("show...");}}
}
3.4.2 静态内部类
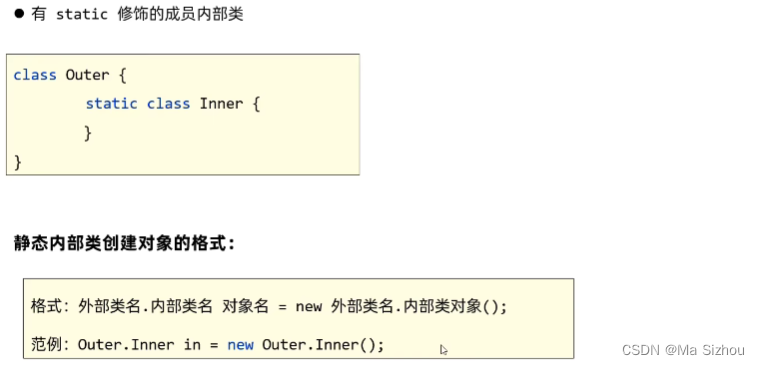
注:其实可以发现,静态内部类与成员内部类主要的区别是,创建对象不同。记住一点:只要是静态的,都是使用类名来调用,理解了这一点,不用刻意记也能知道静态内部类是怎么创建的。
3.4.3 局部内部类
局部内部类是指:放在方法、代码块、构造器等执行体中的类。
下面是一个例子:
class A{public void show(){//B是一个局部内部类class B{int num;}}
}
局部内部类只有在调用此代码块时才会调用到,因此鸡肋,使用较少。
3.4.4 匿名内部类
(1)定义:

注:
- new 类名(){}:代表继承这个类
- new 接口名(){}:代表实现这个类
(2)使用场景:
如果发现在调用一个方法时,此方法的参数是一个接口类型,那么有两种办法解决:
1、定义一个此接口的实现类并重写此方法,然后new这个实现类,最后调用这个方法;
2、使用匿名内部类,即new 接口名(){}。
看下面的例子:
可以发现第二种方法很简洁,因此这就是匿名内部类的使用场景。
对于上述的两种方法,要如何选择呢?
答:如果一个接口的抽象方法很少,则推荐使用匿名内部类,反之使用定义接口实现类的这种方法比较简洁。
4、Lambda表达式
4.1 概述
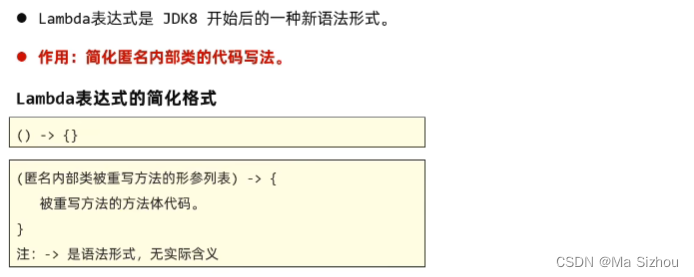
4.2 案例
public class InnerTest {public static void main(String[] args) {//这是匿名内部类useInnerA(new InnerA() {@Overridepublic void show() {System.out.println("我是匿名内部类...");}});//使用Lambda表达式,简化匿名内部类useInnerA(()->{System.out.println("我是使用Lambda表达式的匿名内部类...");});}//这是一个形参类型为接口的方法public static void useInnerA(InnerA a){a.show();}
}interface InnerA{void show();
}
4.3 注意事项


总结:Lambda表达式只能简化只有一个抽象方法的匿名内部类。
4.4 Lambda表达式的省略写法

下面我们一条一来看:
- 参数类型可以省略不写:
//使用Lambda表达式,参数类型可以省略
useInnerA((a, b) -> {System.out.println("我是使用Lambda表达式的匿名内部类...");});
- 只有一个参数,则参数类型可以省略不写,同时()也可以省略
//使用Lambda表达式,只有一个参数,则参数类型可以省略不写,同时()也可以省略
useInnerA(a -> {System.out.println("只有一个参数,则参数类型可以省略不写,同时()也可以省略...");});
- Lambda表达式的方法体只有一行代码,大括号和分号都可省略,同时如果是return则必须省略。
//Lambda表达式的方法体只有一行代码,大括号和分号都可省略,同时如果是return则必须省略。
//返回值为字符串类型,只需要写字符串即可,需要省略return语句。
useInnerA(a-> "我是使用Lambda表达式的匿名内部类...");
4.5 Lambda表达式和匿名内部类的区别

5、窗体、组件、事件
5.1 窗体
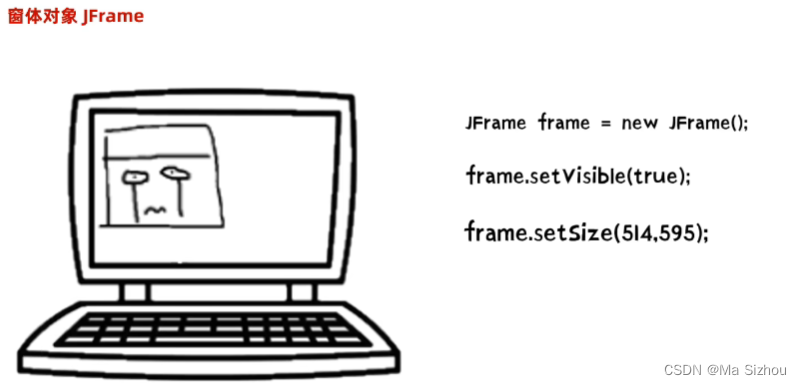
import javax.swing.*;public class JFrameTest {public static void main(String[] args) {//创建窗体对象JFrame jf = new JFrame();//设置窗体大小jf.setSize(511, 511);//修改窗体的关闭模式jf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);//设置窗体标题jf.setTitle("大哥的第一个窗口");//设置窗体可见jf.setVisible(true);}
}
5.2 组件
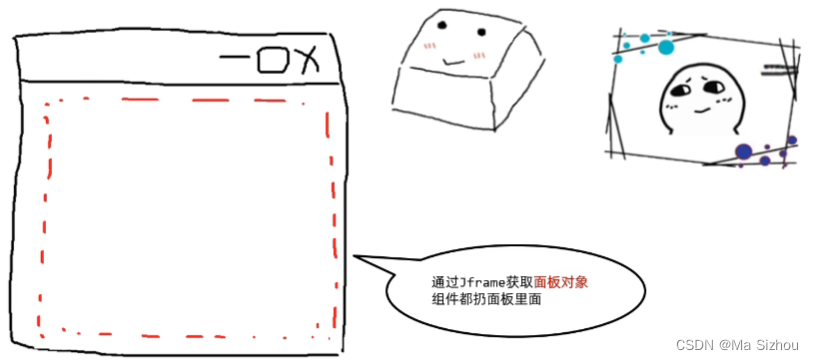

5.2.1 按钮组件Jbutton


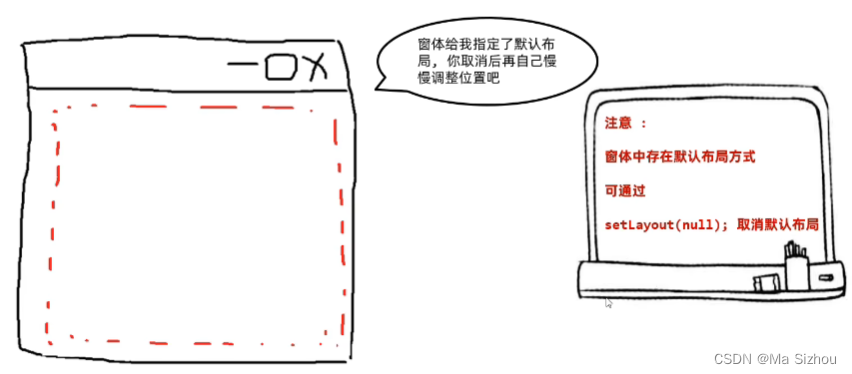
看下面代码:
package com.itheima.frame;import javax.swing.*;public class JFrameTest {public static void main(String[] args) {//1、窗体对象//创建窗体对象JFrame jf = new JFrame();//设置窗体大小jf.setSize(511, 511);//修改窗体的关闭模式jf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);//设置窗体标题jf.setTitle("我是标题");//取消窗体的默认布局jf.setLayout(null);//2、按钮对象//2.1 创建按钮对象JButton jb = new JButton("确定");jb.setBounds(51,51,111,111);//2.2 将按钮对象添加到面板对象当中jf.getContentPane().add(jb);//设置窗体可见jf.setVisible(true);}
}

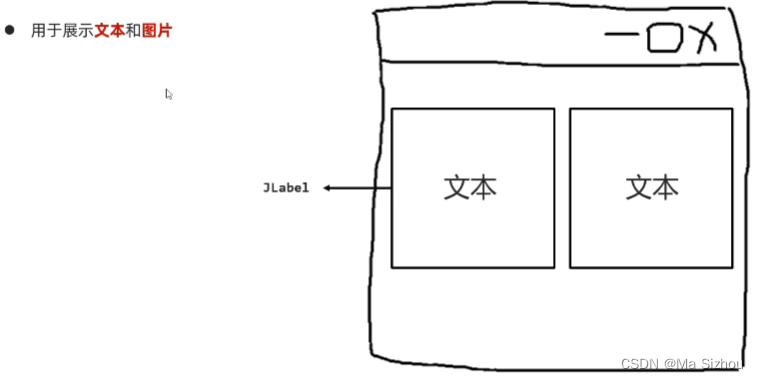
5.2.2 文本组件Jlabel

5.3 事件

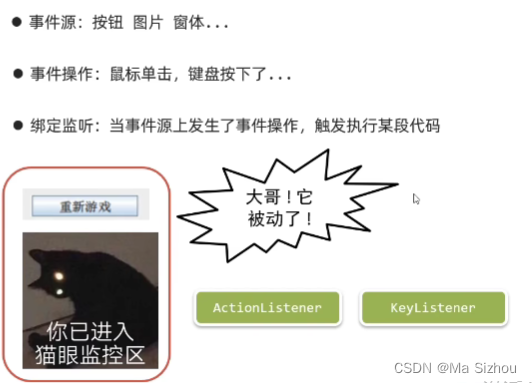
- 动作监听:

package com.itheima.action;import javax.swing.*;
import java.awt.event.ActionEvent;
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;public class ActionTest {public static void main(String[] args) {//1、窗体对象//创建窗体对象JFrame jf = new JFrame();//设置窗体大小jf.setSize(511, 511);//修改窗体的关闭模式jf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);//设置窗体标题jf.setTitle("我是标题");//取消窗体的默认布局jf.setLayout(null);//2、按钮对象//2.1 创建按钮对象JButton jb = new JButton("确定");jb.setBounds(51,51,111,111);//2.2 将按钮对象添加到面板对象当中jf.getContentPane().add(jb);//3、事件监听jb.addActionListener(new AbstractAction() {@Overridepublic void actionPerformed(ActionEvent e) {System.out.println("我被点击了");}});//设置窗体可见jf.setVisible(true);}
}
- 键盘事件:
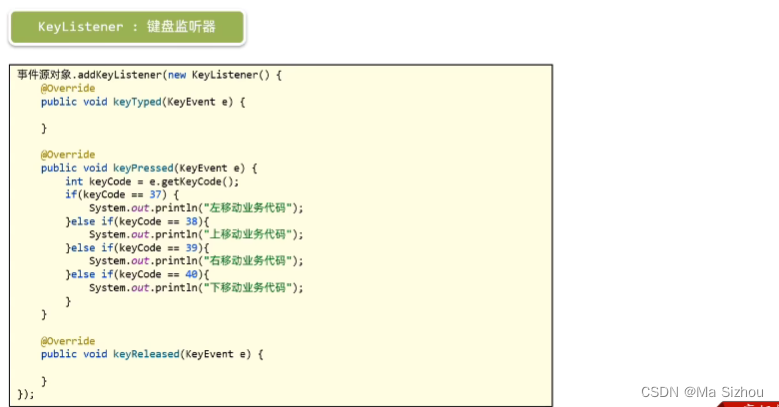
package com.itheima.action;import javax.swing.*;
import java.awt.event.ActionEvent;
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;public class KeyActionTest {public static void main(String[] args) {//1、窗体对象//创建窗体对象JFrame jf = new JFrame();//设置窗体大小jf.setSize(511, 511);//修改窗体的关闭模式jf.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);//设置窗体标题jf.setTitle("我是标题");//取消窗体的默认布局jf.setLayout(null);//键盘事件jf.addKeyListener(new KeyListener() {@Overridepublic void keyTyped(KeyEvent e) {}@Overridepublic void keyPressed(KeyEvent e) {//键盘按下时触发事件int keyCode = e.getKeyCode();if (keyCode == 37){System.out.println("左移动业务...");} else if (keyCode == 38) {System.out.println("上移动业务...");} else if (keyCode == 39) {System.out.println("右移动业务...");} else if (keyCode == 40) {System.out.println("下移动业务...");}}@Overridepublic void keyReleased(KeyEvent e) {//键盘松开时触发事件
// System.out.println("键盘松开了...");}});//设置窗体可见jf.setVisible(true);}
}
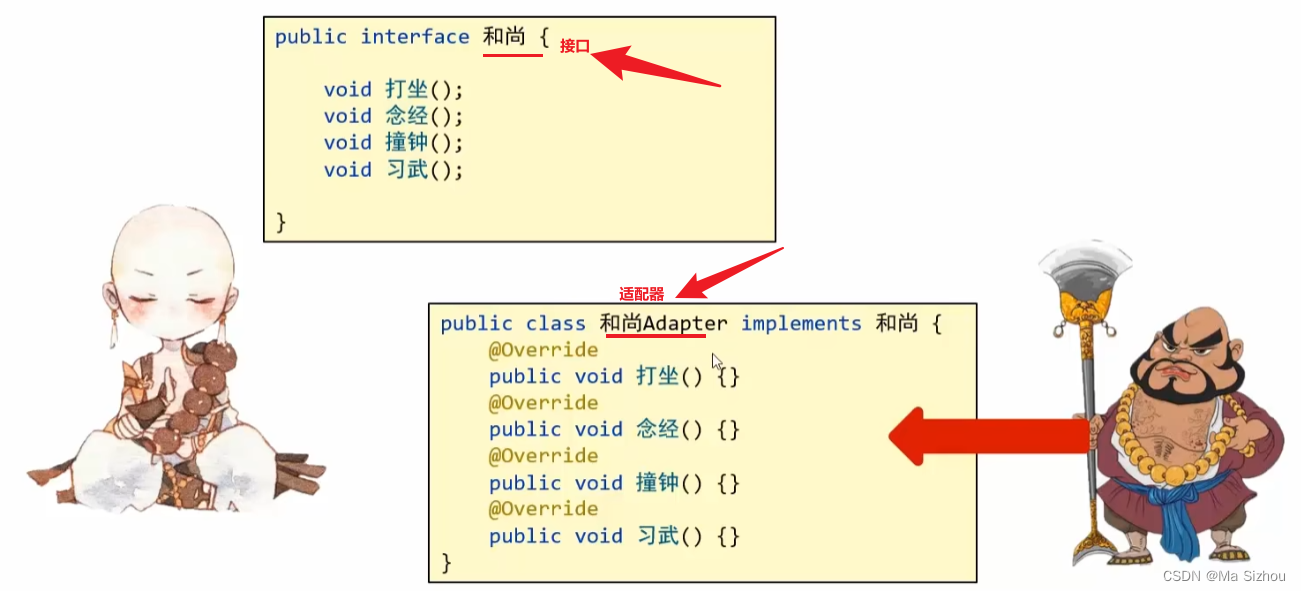
5.4 适配器设计模式

上述对适配器设计模式的描述可能不够清晰,下面再用大白话解释一下:
当我们写了一个接口后,我们会将这个接口进行实现。在进行一个实现时,我们发现无论怎么样,这个实现类是一定要重写接口里的所有方法的,那有什么方法只重写想要的方法呢,这个就是适配器要解决的问题。
- 解决思路:
先编写一个适配器(抽象方法),让适配器来实现这个接口,然后我们要写的实现类只需要继承适配器就可以了,这样我们需要实现哪个方法就重写哪个即可。
如下所示::
- 解决步骤:
5.5 模板设计模式
上面的陈述可能还不是太清晰,下面再通俗的解释一下:
模板设计模式,其实就是先写一个抽象类,然后在抽象类里写一个模板方法,依次调用业务逻辑代码,但是发现有些业务逻辑代码并不通用,于是把这些不通用的代码抽为一个或者几个方法,然后将这几个方法定义为抽象方法,让子类去实现,这样子类就会有各自的业务逻辑,这个就是模板设计模式。
下面看一段代码:
package com.itheima.design.template;public abstract class CompositionTemplate {/*** write方法是模板,但是里面的body是随着每个实现类的不同而不同,因此需要定义为抽象方法*/public void write(){System.out.println("我的爸爸");body();System.out.println("啊~ 这就是我的爸爸~");}abstract void body();
}public class Tom extends CompositionTemplate{@Overridevoid body() {System.out.println("我的爸爸是一个很严肃的人,每天工作很长时间。。。");}
}public class Test {public static void main(String[] args) {Tom t = new Tom();t.write();}
}输出:我的爸爸
我的爸爸是一个很严肃的人,每天工作很长时间。。。
啊~ 这就是我的爸爸~Process finished with exit code 0
注意:上述代码中,要是子类重写了write方法,那岂不是不遵循当初定义的模板了?为了防止重写write方法,可以把write方法定义为最终的,即前面加关键字
final,如下所示:
public abstract class CompositionTemplate {/*** write方法是模板,但是里面的body是随着每个实现类的不同而不同,因此需要定义为抽象方法*/public final void write(){//定义为最终的,防止重写System.out.println("我的爸爸");body();System.out.println("啊~ 这就是我的爸爸~");}abstract void body();
}
但其实业务代码中一般不会这么写死,因为万一你写的模板确实不适合人家的业务需求呢,那岂不是坏大事了。