提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

入行深度学习快2年了,是时间好好总结下基础知识了.现在看可能很多结论和刚学的时候不一样.因此要不断总结和比较

---

1. 线性回归

线性回归本质就是线性规划,高中的时候两条线相交后, 问如何选点和坐标轴围城的面积最大.就是一种.
机器学习中跟常用的是,给几个因素 input ,预测另一个output
比如:受教育程度–>年薪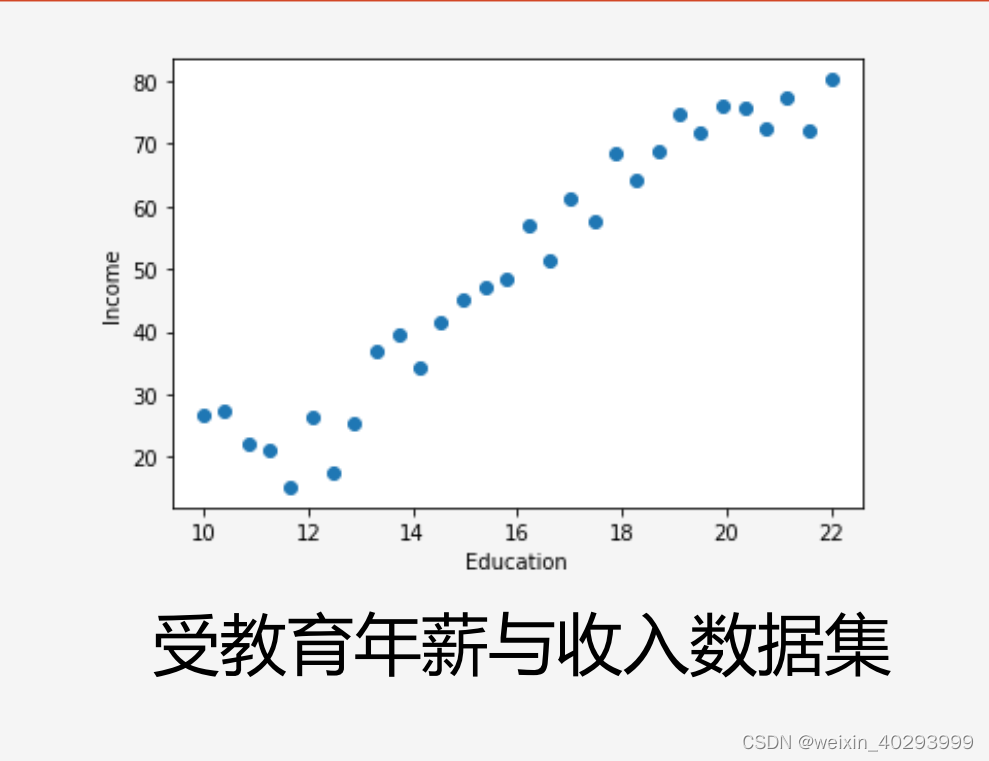
这样就构成了最简单的,单变量线性回归
单变量线性回归算法（比如，x代表学历，f(x)代表收入）：
f(x) = w*x + b
目标是得到这个 f(x) 的系数
系数就是权重, w, b的值.
输出是是预测的收入,
如何评价准不准,模型好不好, 就需要 拿真实的收入和预测的 作差平方求和比较(Loss), 最接近就是好的.
预测目标与损失函数
预测函数f(x)与真实值之间的整体误差最小
如何定义误差最小呢？
损失函数：
使用均方差作为作为成本函数
也就是 预测值和真实值之间差的平方取均值

优化的目标（y代表实际的收入）：
找到合适的 w 和 b ，使得 (f(x) - y)²越小越好
注意：现在求解的是参数 w 和 b

如何优化?? 优化测量：
使用梯度下降算法

2、逻辑回归

什么是逻辑回归 线性回归预测的是一个连续值，逻辑回归给出的”是”和“否”的回答?
其实是和否,是一种概率问题,就是多大的可能性是是,多大的可能性是否.比如 明天下雨的概率, 10%下 90% 不下.
但是我们的f(x) 计算的就是一个连续值啊, 如何转成概率呢,

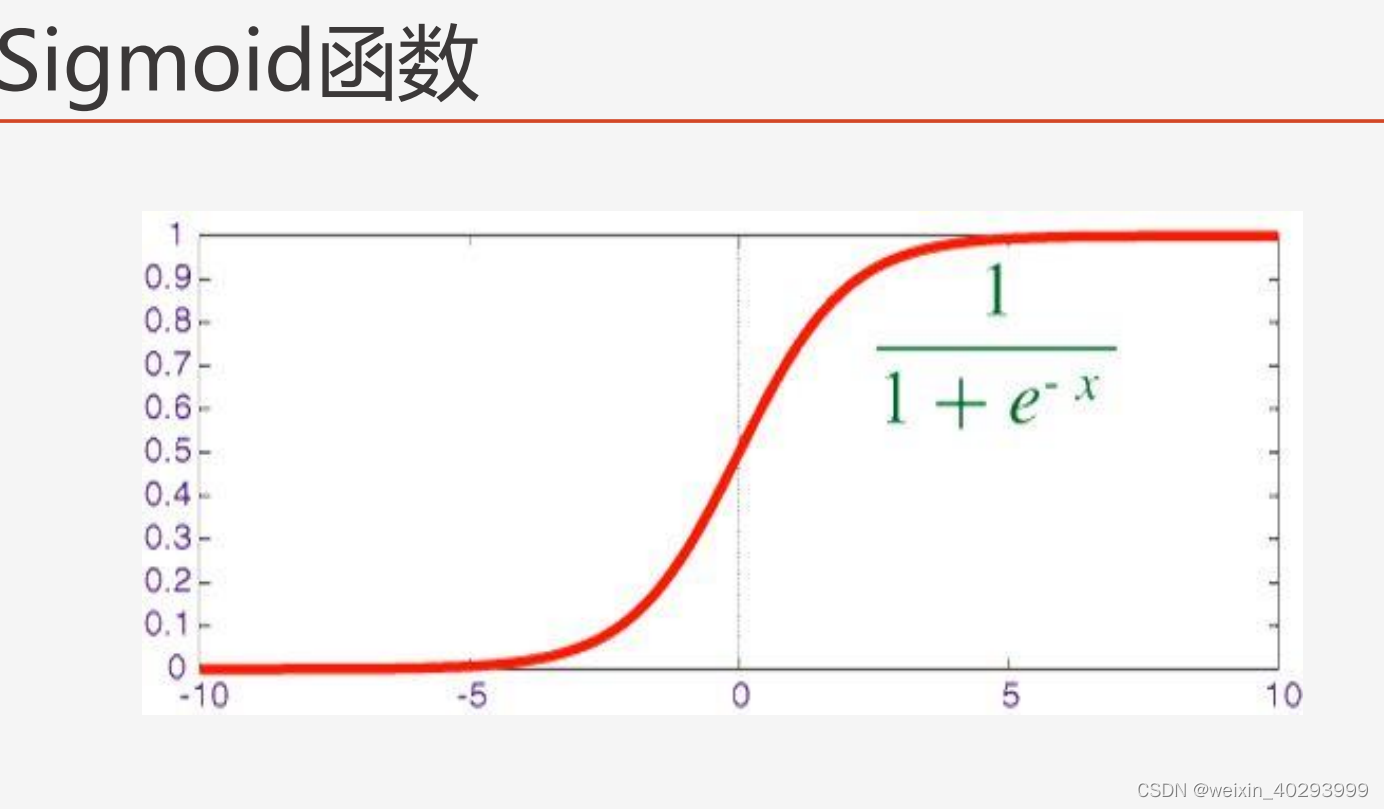
他把给定的所有输入x(其实是f(x)的结果)映射到了0,1直接, >0.5 就是是,小于就是否了.
sigmoid函数是一个概率分布函数，给定某个输入，它将输出为一个概率值

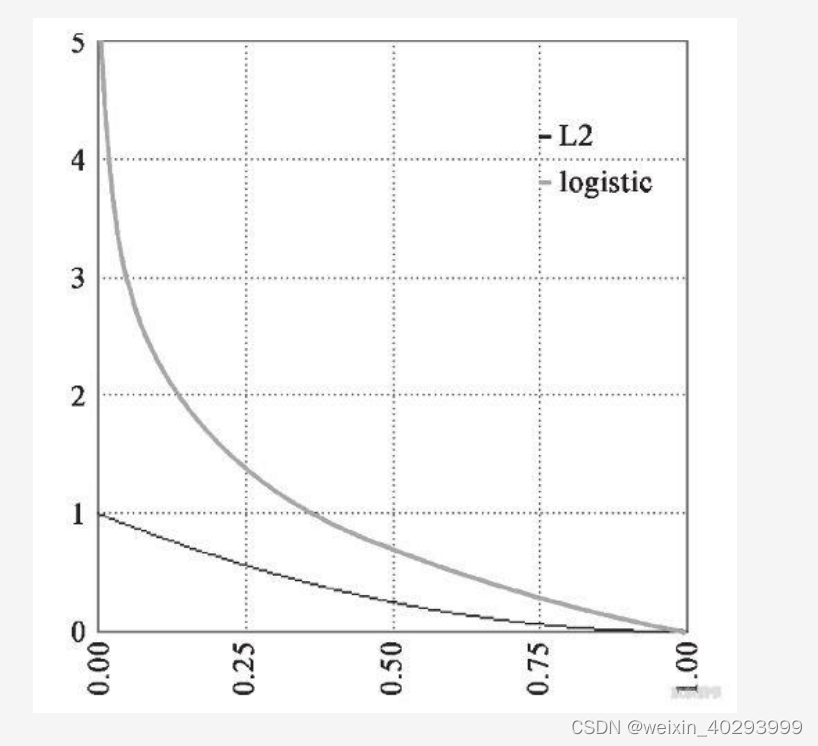
拿到f(x)的结果后,平方差做损失函数线性回归用平方差所惩罚的是与损失为同一数量级的情形.
对于分类问题，我们最好的使用交叉熵损失函数会更有效
交叉熵会输出一个更大的“损失
假设概率分布p为期望输出，概率分布q为实际输出，H(p,q)
为交叉熵，则
交叉熵损失函数

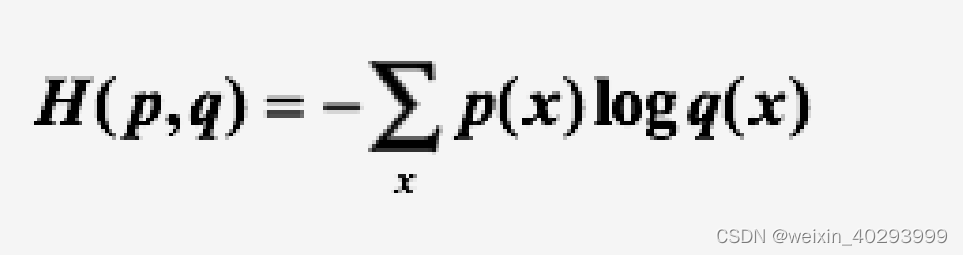
由此可以看到，线性回归和逻辑回归在模型端的区别就是，线性回归输出的是连续值，逻辑回归输出的是（0，1）的概率。 逻辑回归比线性回归多了一个连续值转化为概率的过程.
在优化目标的不同，方差做损失函数和交叉熵损失函数

3. 单层神经元的缺陷&多层感知机

单层神经元的缺陷
无法拟合“异或”运算 异或 问题看似简单，使用单层的神经元确实没有办法解决

原因：神经元要求数据必须是线性可分的,异或 问题无法找到一条直线分割两个类
这个问题是的神经网络的发展停滞了很多年

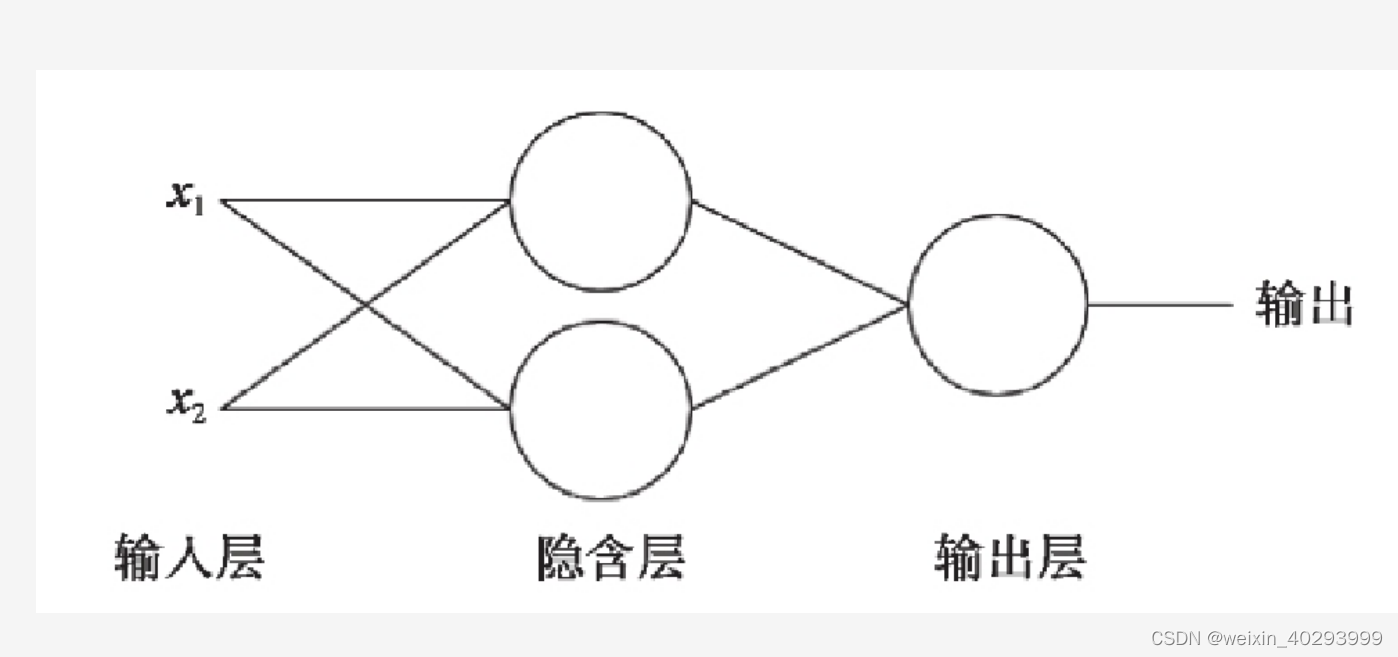
为了继续使用神经网络解决这种不具备线性可分性的问题，采取在神经网络的输入端和输出端之间插入更多的神经元–多层感知机

softmax 多分类

对数几率回归解决的是二分类的问题，
对于多个选项的问题，我们可以使用softmax函数它是对数几率回归在 N 个可能不同的值上的推广.
神经网络的原始输出不是一个概率值，实质上只是输入的数
值做了复杂的加权和与非线性处理之后的一个值而已，那么
如何将这个输出变为概率分布？
这就是Softmax层的作用

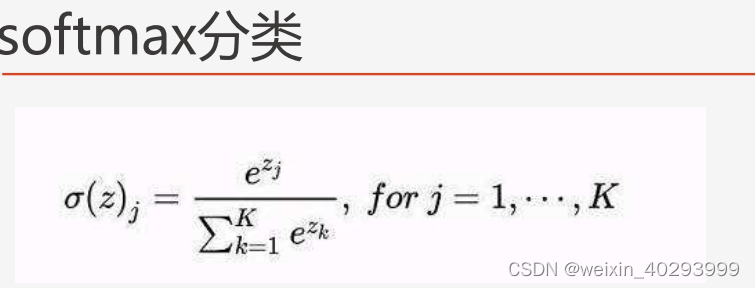
softmax要求每个样本必须属于某个类别，且所有可能的样本均被覆盖
softmax个样本分量之和为 1 当只有两个类别时，与对数几率回归完全相同

opt.step()
opt.zero_grad()
#实际是替代了
with torch.no_grad():for p in model.parameters(): p -= p.grad * lrmodel.zero_grad()

   		loss.backward()#反向传播是记录各个参数变化，后续用来求导opt.step()#利用上一步计算的梯度对内部参数进行更新计算opt.zero_grad()#将梯度归零，便于后面再次迭代计算时不会产生累加现象

最后再来一个 二分类的例子

step 1: 引入库

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import pandas as pd

数据初探:

data = pd.read_csv("./dataset/credit-a.csv",header=None)
data.head(5)

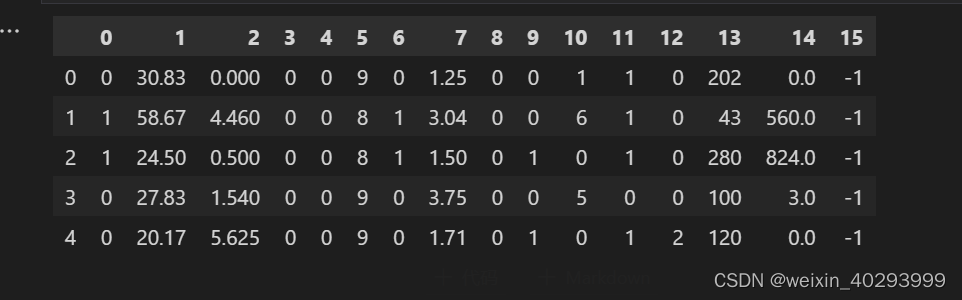
用前15列特征,预测最后一列

# 拆分数据X和y
X = data.iloc[:,:-1]
Y = data.iloc[:,-1]
# 把-1 替换成0 并做数据类型的转换
Y = data.iloc[:,-1].replace(-1, 0)
X = torch.from_numpy(X.values).type(torch.FloatTensor)
Y = torch.from_numpy(Y.values.reshape(-1, 1)).type(torch.FloatTensor)

step2 构建网络:

model = nn.Sequential(nn.Linear(15,1),nn.Sigmoid())
# 二元交叉熵, 二分类 
loss_fn = nn.BCELoss()
# 目标函数,设置目标函数的优化策略
opt = torch.optim.Adam(model.parameters(), lr=0.0001)

step3 训练:

batches = 16
# 整除的方式, 不足一个batch的就舍掉,比如0.25
no_of_batches = len(Y)//16for epoch in range(1000):total_loss = 0for batch in range(no_of_batches):# 起始位置start = batch*batchesend = start + batches# start = batch*batches# end = start + batchesx = X[start: end]y = Y[start: end]# 计算lossy_pred = model(x)loss = loss_fn(y_pred, y)total_loss+=loss.item()opt.zero_grad()loss.backward()opt.step()# 实际预测结果print(epoch,"acc",((model(X).data.numpy() > 0.5).astype('int')==Y.numpy()).mean())print(epoch,"loss",total_loss)

查看训练的权重参数:

model.state_dict()

step4:实际的结果

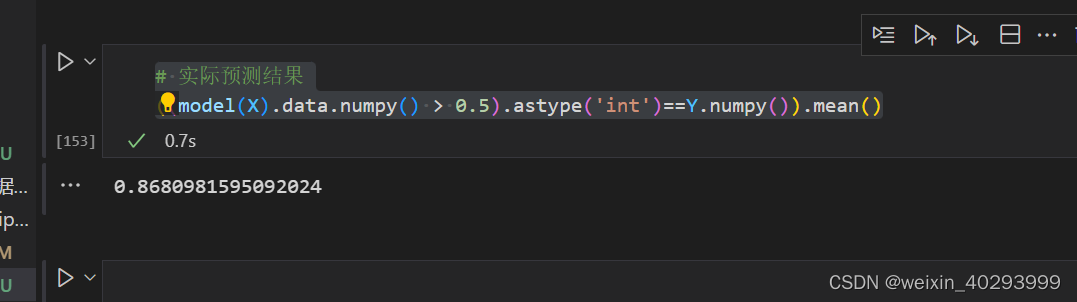
# 实际预测结果
((model(X).data.numpy() > 0.5).astype('int')==Y.numpy()).mean()