长沙便宜做网站品牌推广服务

毫末智行是一家致力于自动驾驶的人工智能技术公司,其前身是长城汽车智能驾驶前瞻分部,以零事故、零拥堵、自由出行和高效物流为目标,助力合作伙伴重塑和全面升级整个社会的出行及物流方式。
在自动驾驶领域中,是什么原因让毫末智行放弃了 MySQL 而选用分布式数据库?在进行分布式数据库选型的时候,为什么选择了 OceanBase ?毫末智行运维工程师赵国良分享了这一数据库替换到落地的历程和实践经验。

(一)数据的产生
在毫末智行大数据环境的组织机构业务中,数据的流转主要可以分为三个周期:数据采集、数据处理和数据管理。在每个不同周期,数据也都具备其相应特点:
-
数据采集:存在车型多样、解析规则复杂、数据包体积大、需要永久保留等特点。
-
数据处理:存在数据量大、时效性要求高,处理过程复杂等特点。
-
数据管理:根据业务特性、数据属性、成本等多个维度,决定了数据管理的复杂度极高。
其中数据采集部分比较抽象,难以理解,因此,我们将以毫末智行自身的案例为例,详细讲解数据采集阶段的具体情况,包括:不同的数据应该如何分配任务给不同的车型、如何根据车型和硬件信息来制定解析规则、为什么需要永久保留采集到的数据。
首先,在数据采集中,不同的车型会根据其所分配的任务去采集数据。这些车型可能包括家用轿车、SUV、越野等不同类型。其次,根据车型、硬件型号、雷达位置或图像收集位置等信息,需要制定一个详细的解析规则。由于需要考虑各种因素,这个解析规则可能相对复杂。最后,要将收集到的数据进行永久保留处理。因为在整个训练过程中,为了应对各种不同的训练场景,数据经常会通过筛选的方式被反复使用。
正是因为在数据产生过程中存在以上种种难点及问题,毫末智行逐渐萌生了从 MySQL 逐渐转为分布式数据库的想法。
(二)数据的处理和使用
我们的数据处理和使用可以划分为四个阶段:
第一阶段是脱敏阶段。在采集回来的数据,先逐帧进行敏感的数据定位和模糊,并且将数据中存在的敏感数据脱离。
第二阶段是推理阶段。在脱敏完成后,会进入推理阶段,这时需要在每一帧的数据上进行打标签分类,并对标签进行管理,便于以后的数据查询和筛选使用。
第三阶段是标注阶段。在推理阶段完成之后,进入标注阶段,在这个标注阶段需要逐帧进行自动标注或者人工检查,同时需要追踪数据的流动。
第四阶段是训练阶段。在标注阶段完成后,数据集将进行模型训练,并追踪数据的使用情况。
(三)数据处理应用场景
数据处理阶段是大数据应用中的核心环节之一,数据处理过程复杂,且数据标注具有时效性高、数据量大等特点。以下图为例,它是对数据处理阶段的一个简单概述。
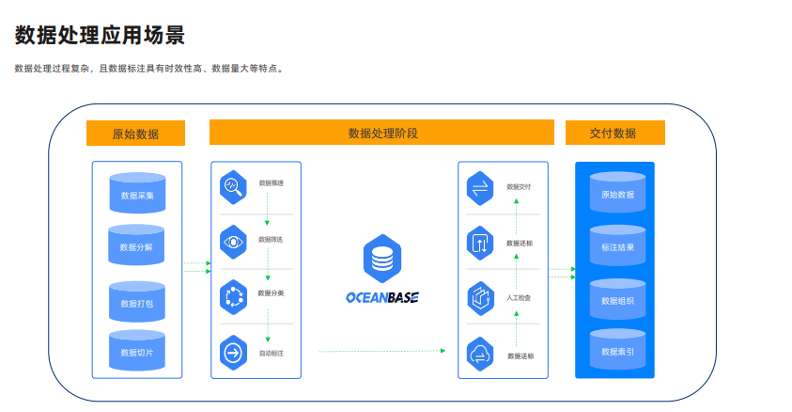
从图中可以看出,数据处理过程包括左侧原始数据中的数据采集、分解、打包到切片的步骤开始,以及数据推理、筛选、分类、自动标注,直到最终数据交付等步骤。整个过程相对复杂,且数据量大。
然而当数据交付完成后,仍然需要保留原始数据、标注结果、数据组织以及数据索引等操作。MySQL 的设计目标是面向 OLTP 场景,遇到处理这种量级的大数据量时会遇到性能瓶颈,且 MySQL 的扩展方式比较复杂,难以满足数据处理阶段对扩展性的要求。基于上述挑战,毫末智行决定选用分布式数据库技术路线,解决数据库的性能、扩展性、可用性和数据一致性问题。

由于公司规模和云环境的庞杂,数据管理对于公司来讲可能逐渐成为了一个严峻的任务,特别是当一个人负责多个云上的 RDS 产品和自建 MySQL 实例时,管理难度会进一步提升。以毫末智行为例,我们公司是基于多云的环境下,每个云上都有 RDS 产品,以及自建的 MySQL 主从实例。由少数或者单个运维单独负责数据管理部分,不仅工作量比较大,还会出现难以集中管理的问题。特别是,当公司数据量过亿之后,MySQL 的性能就会显得较为吃力。目前,公司数据量还会以每年 5 亿的速度不断增长,这将对公司的数据管理带来更大的压力和挑战。
另外由于存在大量的范围查询,导致 MySQL 频繁告警的问题,无论是从运维或者研发的角度来看,单独抽出时间和精力,利用分库分表或者其他方式进行解决告警频繁问题所付出的成本过高,并且时间和精力也有限。因此,这也就是为什么毫末智行要坚持选用分布式数据库的原因。在选择分布式数据库的过程中,毫末智行也了解过一些其他数据库,但相比之下,团队认为 OceanBase 更适合毫末智行的业务环境。
毫末智行选择 OceanBase 主要是因为它具备了以下核心能力:原生支持多租户架构及资源隔离能力、可视化管控、高度兼容 MySQL 生态等。OceanBase 自身的集群资源管控能力相比于我们测试的其他数据库更加优秀,它的租户按需分配等特性也更加符合我们的实际业务需求。迁移至 OceanBase 后,为业务带来了以下改善:
-
高可用:毫末智行一直使用公有云,最早的 OceanBase 集群已稳定运行了六个月,虽然期间经历了一次公有云的故障,但由于 OceanBase 自身的高可用特性,业务并未受到严重影响。
-
降低成本:使用 OceanBase 后,云端成本从使用 MySQL、RDS 时的 10 万/月缩减至使用 OceanBase 时的 4 万+/月。此外,通过自动化和智能化的管理方式,OceanBase 简化了运维流程,减少了人工干预和操作成本。特别是在公司数据量增长或业务调整时期,解决了之前 MySQL 告警频繁的问题,帮助运维人员减轻了大量的工作负担。
-
易于管理:在 采用 OceanBase 之前,运维人员需要自行进入公有云 A 或公有云 B 中分别进行管理,或者是登录 ECS 服务器去集中管理,这种方式非常复杂且不方便。采用 OceanBase 后,我们可以利用 OCP 进行集中管理多个集群或在一个集群中管理多个租户,这样就实现了对所有实例的统一管理。之所以没有选择 OCP Express 是因为它只能接管单一集群,而我们公司已经有多个集群的规划,所以选择了 OCP。
-
灵活调整:在灵活调整方面,其实公有云 20S 也可以做到灵活调整,但考虑到可能会存在较短时间的网络抖动风险,我们尽量避免不必要的风险对数据库造成潜在影响。OceanBase 的多租户特性可以很好地根据公司业务高峰或低峰快速调整资源并重新进行分配,大大减少了配置变更所带来的风险。
-
性能提升:OceanBase 的性能也超出了我们的预期。在 MySQL 操作上亿条数据时,即使有索引,SQL 执行时间至少会停留一分钟。经我们的实际测试,将数据迁移到 OceanBase 后,即使是超长的慢 SQL ,执行时间能够保持在 2 ~ 5 秒之间。

(一)OceanBase 的架构特征
在落地部署 OceanBase 之前,我们首先需要了解其架构特性和工作流程。当一个访问请求进入系统后,会通过负载均衡器将请求数据转发到 OBProxy 中,再根据 SQL 的路由转发功能,请求会被分布到系统内各个 Zone 中的 Server 节点进行处理。
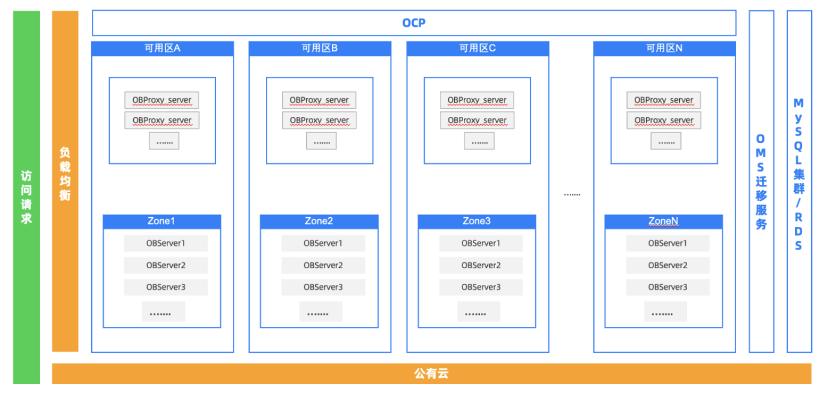
OceanBase 架构中的一些特征让它具有很高的灵活性和可靠性:
-
支持多云基础设施:OceanBase 是 share-nothing 架构,同时多租户的特性相当于具备了云的弹性和资源池化特性。这意味着它充分利用了云计算的弹性、可扩展性和高可用性。能够适配多云平台上基于基础设施的各类存储系统,为企业提供了更加灵活和可靠的数据存储和处理能力。
-
多副本策略:为了提高数据的可靠性和可用性,OceanBase 采用了多副本策略。这意味着数据在多个位置都有副本,可以防止某个位置的数据丢失或损坏。这种策略避免单点故障带来的停机风险,在确保数据的完整性和一致性的同时,提高了系统的可用性和容错性。
-
同城多活架构:在多副本策略的基础上,OceanBase 实现了同城多活架构。这意味着即使在一个城市内,不同的机房也可以作为数据副本的存储位置。这种架构确保了即使某个机房发生故障,系统仍然可以正常运行,并提供了高可用性和容错能力。
-
OMS 迁移工具:OMS 是 OceanBase 提供的一种第三方迁移工具。这种工具可以用于将数据从一个云环境迁移到另一个云环境,或者从一个数据库迁移到另一个数据库。与传统的迁移工具相比,OMS 提供了更高的定制性,可以根据企业的需求进行定制化的迁移和数据对比。
综上所述,从 OceanBase 的技术特征来看,不但拥有分布式数据库的可扩展性,又具备集中式数据库的单机性能,在业务需求上兼具可扩展性、高可用性以及可调度性,能满足企业在不同发展阶段、不同场景当中对于数据库的不同要求。
(二)基于混合云的同城多活架构
上面主要介绍了 OceanBase 架构的多个特征。接下来会详细说明下基于混合云的同城多活架构。同城多活架构通过利用 OMS 工具进行数据迁移,我们能够将数据从 MySQL 集群迁移到与它匹配的 OceanBase 集群,确保迁移过程中的数据完整性和准确性。这种迁移过程的高效性和定制性,使得企业能够根据自身需求进行数据管理和处理,并提供更好的数据管理和处理能力。
此外,OCP 集中管控工具的使用也为我们提供了更好的管理和监控能力。通过集中管控,能够更好地管理和监控各个集群的状态和性能,确保系统的稳定性和可靠性。
在过去半年中,我们完成了数个超 10 亿行数据的表的迁移工作,进一步证明了 OceanBase 的强大功能和卓越性能。这种大规模的数据迁移需要高度的技术能力和精细的管理,而 OceanBase 和 OMS 数据迁移工具的结合,使得这种迁移变得相对简单和高效。
因此,对于 OMS 工具的优秀表现和卓越性能,确实值得表扬。它为毫末智行提供了高效、可靠和可扩展的数据存储和处理解决方案,并为企业带来了更好的数据管理和处理能力。

OceanBase 的落地为毫末智行带来了多方面的收益,包括:
-
更强的数据可靠性和可用性
OceanBase 实现了城市级别的容灾,相比于传统的 RDS 服务,OceanBase 在容灾方面具有更强的能力,能够更好地应对各种故障和灾难场景,确保业务的连续性和稳定性。
-
更强的扩展性
OceanBase 具备动态扩容的能力,能够实现无感知的平滑扩容。这种特性使得企业在数据量增长或业务调整时期能够快速响应需求,而无需进行繁琐的扩容操作,使得企业能够更好地应对业务增长和变化。
-
更低的运维成本
OceanBase 通过自动化和智能化的管理方式,能够简化运维流程,减少人工干预和操作成本。特别是在数据量增长或业务调整时期,解决过往 MySQL 告警频繁的问题,从而帮助运维人员减轻大量的工作负担。
-
更低的云成本
与传统的 MySQL 或 RDS 相比,OceanBase 在存储成本和费用成本方面都有显著的缩减。云端成本从之前的约 10w/月缩减至 4w+/月,这为企业节省大量的成本,并提高资源的利用效率。
总的来说,OceanBase 的落地为企业带来了多方面的收益,包括实现城市级别的容灾、动态扩容能力、降低运维管理成本以及降低云的成本等。这些收益有助于企业提高业务的连续性和扩展性,降低成本并提高资源利用效率。

迁移至 OceanBase 后,企业能够获得多方面的显著收益,但在落地过程中会遇到一些挑战。以下是一些常见问题和解决方案:
首先,OCP 接管问题。OCP 接管 OBD 方式部署集群时会存在权限问题。这是因为 OBD 是使用 root 用户进行部署,而 OCP 则要求使用普通用户进行操作。由于OBD 和 OCP 的权限管理方式存在差异,因此在利用 OCP 接管其他集群时,需要确保使用正确的用户进行操作,否则就会出现权限不足的问题。
其次,部署问题。OCP 的备份功能能够确保数据的可靠性和恢复性。但当 OCP 云部署集群时,可能会发现集群备份没有可恢复的时间区显示值。这可能是由于 ob_admin 文件的位置问题导致的。ob_admin 文件是 OCP 用于管理备份的重要文件,它记录了备份的相关信息。当 ob_admin 文件位于 temp 目录下时,它可能无法正确地记录备份的时间信息,从而导致没有可恢复的时间区显示值的问题。
最后,升级问题。OCP 升级 4.2.1 版本双节点 Agent 自动升级任务失败。这是因为在升级时,如果选择单独升级了 A 节点,之后手动升级 B 节点,就会导致 Agent 自动升级时任务失败。并且当自动升级失败之后,缺乏批量操作功能无法直接跳过失败任务,只能逐一手动完成操作任务,还是比较遗憾的。

当前,毫末智行的数据量约为 20PB ,数据对象接近 60 亿。基于过去一年的增长趋势,以及现在的采集和业务规划,预计数据对象的体积将会翻倍,三年之后可能会达到 180 亿。
而在这些数据当中,目前它的强管理数据约为 2 亿,预计三年之后它会增加至6亿。针对以上数据相关的索引、特性、标签、地址等一系列内容都会在 OceanBase 当中进行存储。因为 OceanBase 具有高效的数据存储和处理能力,能够应对数据量增长和数据复杂性的挑战。这也是毫末智行选择 OceanBase 的理由之一。未来,对于 OCP、ODC 和 OMS 三个数据库管理平台,也有一些想法和规划:
首先,我们想基于 OCP、ODC 和 OMS 打造一个支持 Web 可视化的数据库管理平台。通过 OCP 对 OceanBase 提供的集群图形化管理能力,包括数据库组件及相关资源的全生命周期管理,故障恢复,性能诊断,监控告警等功能,不仅降低IT运维成本与学习成本,也能够提高工作效率。
其次,我们想利用 ODC Web 版,完成数据库审计、数据安全管理和基础数据开发等工作需求。尤其是在数据安全管理和基础数据的开发等需求场景下,数据库审计是非常必要的。虽然目前没有时间去深入探索 ODC 的一些功能,但已经把这项工作加入未来工作规划中。
最后,我们想利用 OMS 低风险、低成本、高效率的数据流通特性,将目前剩余未迁移的 MySQL 数据,全部迁移至 OceanBase 中。OMS 不仅可以节省大量的时间精力,还可以让业务数据建立在安全、稳定、高效的数据复制架构之上。这也是我们非常满意 OMS 的原因。
