福永外贸网站建设唐山网站制作app
大家好,我是良许,新年快乐呀~
在我女室友坚持不懈的努力之下,2022年的最后一天我终于被她传染了,阳了~
此时的我,正顶着37多度的低烧写下这篇年终总结。
2022年,对于大多数人而言,封控是主旋律——不停地核酸,不停地居家。特别是对于做实体行业的小伙伴,真的是损失惨重。
我在广州租住的地方有个步行街,我就亲眼看着那边的店铺一家家新开,又一家家倒闭。甚至看到新开的店铺,我就跟女室友打赌,赌它什么时候倒闭。
但是,像我这种做自媒体的,封控对我来讲几乎没任何影响。不就居家嘛,给我一台电脑,一根网线,我在月球都可以办公。
说没影响也是假的,大环境不好的情况下,谁都无法独善其身。现在也完全放开了,不论好坏,我们都应该接受这个事实。
好了,不说这个客观的大环境了,跟大家分享我的2022年吧。我的2022年真的可以用翻天覆地来形容,当然有好的一面,也有不好的一面。
在这一年里,我从广州搬回了福州,在短视频和直播领域扎根下来,并且也进军了知识付费。
1. 离开广州
2017年7月初,我从厦门搬去了广州,2022年7月初,我又从广州回归福州,在广州呆了整整5年。
良许离开广州
很多人问我为什么离开广州,广州毕竟是一线城市,各方面的资源都比福州好,而且也有很多投资人想投资我做点小事情。
的确,在广州我也认识了很多大佬,见过很多公司老板、高管,也结交了很多跟我一样的创业者,并且也有跟身价几亿的投资人畅聊行业趋势。
但对于我来讲,在广州,总有点漂的感觉,没有真正安定下来。虽然我也有能力在广州安家落户,但总是觉得这里不是我真正的家。
现在我回到福州了,虽然比不上广州,但这里的一切我都觉得非常亲切。而且现在住进了自己买的房子里,一切都是那么踏实而安定。
良许乔迁新居啦~
虽然我回到了二线城市,但在广州的5年,我的个人能力也得到了飞速的提升,也是我从一名普通打工者蜕变成创业者的地方。
所以,我依然还是鼓励年轻人,一定要去大城市,哪怕是闯荡几年也行,这会极大开阔你的视野和眼界。
2. 公众号
熟悉我的朋友都知道,我是做公众号起家的。从2018年6月到现在已经四年半了,而且我也会坚持写下去。
在公众号这个平台,我赚到了人生的第一个百万,也通过公众号我被很多人认识,同时也结交了很多大牛,所以我对公众号一直都非常有感情的。
但是随着短视频和直播的冲击,现在公众号的整体数据一直在稳步下降。
我在只有14W粉丝的时候,平均阅读量上万。而现在,我已经接近22W粉丝,平均阅读量也只有六七千。
没错,粉丝涨了,阅读量反而跌了。
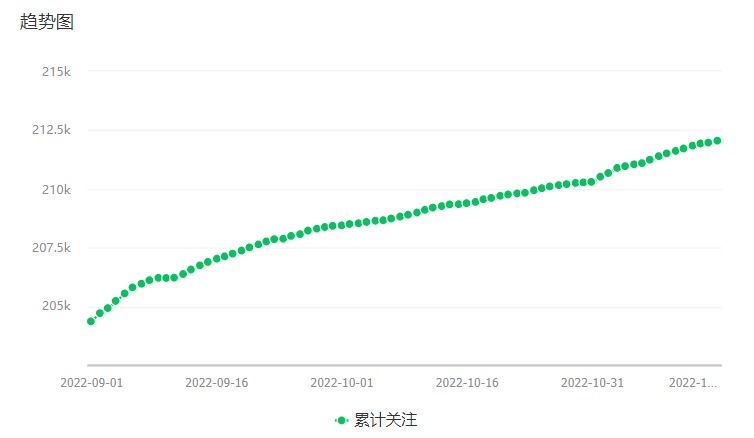
当然,也可能因为我最近原创变少的原因(忙于做视频,精力有限)。
而且,公众号的行情也在变差。不知道大家有没发现,这一年来很多公众号发的广告越来越少了,甚至不少号已经卖身或停更?
说实话,无利不起早,当你赚不到钱的时候,你就没有更新的动力了。
别跟我讲情怀,那些说自己写公众号是因为情怀的,我没见哪一个坚持下来的。
不瞒大家说,我从公众号赚到的钱,也一样减少了好几成。但我不会放弃的,公众号就是我的后花园,粉丝就是我的老朋友,偶尔跟老朋友聊聊天也是非常开心的事。
最近忙于录课,原创少了些,等我录完课我就多更新一些干货,大家等我哈~
3. 短视频
在两年前我就已经探索短视频,但由于方法方式不对,一直没做起来。
在年前年初的时候,我潜心钻研各种教程,研究各种套路,精心打磨视频,今年我的短视频终于迎来了爆发!
我的重点是抖音,但各个短视频平台也在同步更新(视频号、快手、小红书、B站)。
前几个月我稍微算了下,这几个平台一起涨粉了15W左右,而公众号涨到15W我用了近4年,可见短视频的威力所在。
现在我在抖音随便发个视频,都有一两万的播放量,而同样的内容在公众号只有七八千。
所以,2022年我非常重视短视频这个平台,选题、写稿、拍摄、剪辑,每个环节都要花费大量的时间,所以我也是我公众号原创下降的原因,毕竟精力有限嘛。
但是,虽然涨了这么多粉,我在短视频里基本上没赚到钱,这也是我用的方法不对吧。
但不管怎样,短视频是趋势,先把它做起来再说。当时我刚进军抖音的时候,我也不知道怎么赚钱,但我知道这是趋势。
4. 直播
今年3月,我参加生财有术团队的抖音直播大航海,从那个时候开始直播,一直坚持到现在,几乎没有断播过。
我这人最大的优点就是——特别能坚持。当时同期的1800多个船友,能坚持直播到现在的,估计不到100人,甚至更少。
刚开始直播的时候,只有一两人在线,现在场观基本稳定在2~3W。在5月份的时候,在线人数甚至一度超过3300人,而且还被生财老板亦仁发现,并在内部进行宣传。

一开始我做直播也是没赚到钱的,但我还是依然坚持直播。还是那句话,我相信这是趋势。
除了自己坚持直播,我每天还偷偷录制对标账号的直播,学习他们的内容、话术,然后应用在自己的直播间。
如果有经常来我直播间的小伙伴,应该有发现我的直播风格更换了好几款,这就是不停学习、不停迭代的结果。
未来,我还是会坚持直播下去,无它,就是脸皮厚而已。
5. 知识付费
刚开始做短视频和直播,一直都没有自己的变现产品,所以空有流量也愁于转化。
在5月份时,我花了一个半月的时间,录制了一套Linux命令的课程,介绍了150个常用命令的用法。
这套课程内容很干,录制虽然花了一个半月,但前期的准备也花了很久。这也是我做知识付费的一个探索。
本来我想卖68元,但经过小调查,发现大家普遍觉得命令用到再百度即可。算了,我也懒得多说什么了,就卖9.9元得了,交个朋友。
学习Linux命令的正确姿势
回到福州之后,我见了同在福州的抖音号主「上官社长」,跟他聊了一下午,交谈甚欢,于是一拍即合,一起联手做嵌入式培训!
 于是第二天,我就搬进他的公司办公,就是这么干脆利落!
于是第二天,我就搬进他的公司办公,就是这么干脆利落!
上官老师虽然只比我大一岁,但他的经验、阅历、眼界,都远高于我。虽然我们是合作关系,但我一直尊他为良师。
做职业教育,肯定离不开被说割韭菜。但是,为知识、为服务而付费在现在这个时代是再正常不过的事情,我希望大家能辩证看待这个问题。
收了钱,不做事,那是纯纯的割韭菜;但是收了钱,我把你培养成一名嵌入式工程师,这是多么双赢的一件事?
涨粉5.5W,良许又开始搞事了…….
6. 小小的总结
很多人说2022年很操蛋,但是对于一个创业者而言,没有经历过一些波澜,怎么对得起「创业」这个头衔?
2022年过去了,很多人拍手叫好,但说实话,我非常不舍!虽然2022年有很多黑天鹅事件,而且口罩事件让大家叫苦连天,但——
这才是人生!
2022年虽然一切都处于低迷,但一样的N多人发大财(国难财除外)。说因为疫情而没有赚到钱的,那只是你的借口罢了。
而且——现在放开了,你连这个借口都没有了……
2018年开始我边上班边创业,2020年我全职创业,现在已经被社会毒打两年了。
虽然我是做自媒体,但我一直都是做程序员这个赛道,所以我依然没有脱离程序员这个身份,完美将兴趣与赚钱结合。
2023年我就不立flag了,一方面怕被打脸,另一方面我也不喜欢立flag。
我只有一个心愿,让家人平安健康,不愁吃,不愁穿,日子不要过得紧巴巴,就够了!(貌似已经实现了?)
2023年,一起加油!
学习编程,千万不要急于求成,一定要多读一些经典书籍,多看源码,多下苦功夫去死磕代码,这样技术才能长进。给大家分享一些程序员必读经典书籍,一定要多读几遍:

免费送给大家,只求大家金指给我点个赞!
程序员必读经典书单(高清PDF版)
有收获?希望老铁们来个三连击,给更多的人看到这篇文章
推荐阅读:
- 干货 | 程序员进阶架构师必备资源免费送
- 刷题 | LeetCode算法刷题神器,看完 BAT 随你挑!
欢迎关注我的博客:良许Linux教程网,满满都是干货!
