雄县做网站logo设计在线生成免费商标
报错内容如下图:

Windows 系统会对全局安装的脚本进行一个限制,防止恶意脚本执行,所以此处会报错。
如何解决?通过修改 windows 执行策略来解决此问题。
一、什么是 windows 执行策略
Windows 给 PowerShell 设定了一个叫 “执行策略” 的东西。为了避免一些恶意脚本直接运行,一般电脑的 windows 系统默认将执行策略设置成了 Restricted,即受限制的。
所有的执行策略如下所示:
- AllSigned:要求所有脚本和配置文件均需受信任的发布者签名,包括在本地计算机上编写的脚本。(安全但是本地编写的脚本也要签名,麻烦)
- Bypass:不会阻止你运行任何脚本,也没有提示和警告。(不安全)
- Default:默认的执行策略;普通桌面Windows默认Restricted,服务器windows默认RemoteSigned。
- RemoteSigned:要求从互联网上下载的所有脚本和配置文件均需要受信任的发布者签名,本地脚本则不需要签名。是Windows服务器的默认执行策略。(较为安全)
- Restricted:无法加载配置文件或运行脚本。桌面Windows的默认执行策略。(安全,但无法运行脚本)
- Unrestricted:允许所有的脚本运行。
若要按优先级顺序显示每个范围的执行策略,请使用 Get-ExecutionPolicy -List 。
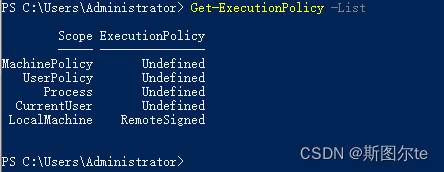
若要查看 PowerShell 会话的有效执行策略,请使用 Get-ExecutionPolicy 不带参数的。

windows执行策略参考: Learn/PowerShell/脚本编写/参考/Microsoft.PowerShell.Security
二、解决方式
-
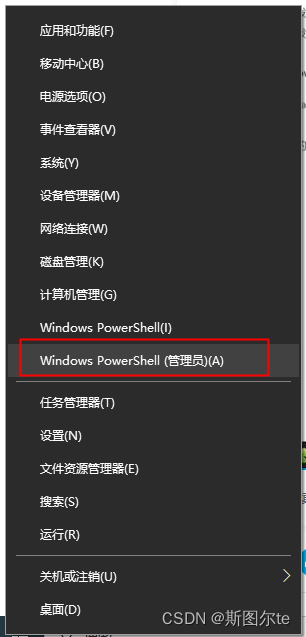
鼠标右键 windows 键(电脑左下角),以管理员身份打开 PowerShell:
-
可以先查看一下当前的执行策略
get-ExecutionPolicy,结果显示是受限制的:

-
修改执行策略,输入指令
set-ExecutionPolicy RemoteSigned,
这里指令其实是不区分大小写的,完全可以写成set-executionpolicy remotesigned;

输入A,点击 enter 键确认;

-
查看是否修改成功 windows 执行策略,输入
get-ExecutionPolicy,显示修改成功:

-
重新执行
nodemon -v:

