海口建设工程信息网站建筑业企业所得税2%
震动刀切割设备是一种利用振动刀片在各种非金属材料表面上切割的设备,振动刀切割机利用刀片高频振动和360度旋转,能保证每分钟上万次的振动频率,可在平面进行垂直切割,锋利裁剪。震动刀切割设备切割速度快,可以单层切割和多层切割,可以大大提高产品生产的速度和量产的效率,非常适合用于大批量的产品;由于振动刀切割机的刀片振动频率非常高,而且振动幅度小,加上运行稳定,切割精度高,非常的灵活,适用性非常广泛,可以在聚氨酯泡棉、硅橡胶、橡胶片、泡棉、海绵、塑料薄膜、纸品包装、广告标识、纺织面料等材料上进行垂直切割,加工成设计的形状和大小。
震动刀切割设备切割速度快,且可以单层切割多层切割 ,可以大大提高产品生产的速度和量产的效率,非常适合用于大批量的产品;该设备具有无烟无味无粉尘等特点,是一种先进的环保切割技术,深受企业喜爱,具有广阔的市场。
当前全球已步入数字经济时代,震动刀加工作为一种先进的加工技术,具有智能化、标准化、连续性等特点,易于与精密机械、精密测量技术和电子计算机相结合,能够与工业机器人等进行自动化集成,实现精密加工的高度自动化和智能化,从而提高加工效率。
我国传统制造业正处于加速转型阶段,震动刀加工设备作为智能化与自动化结合的重要设备,将助鞋履制造、服装纺织等传统制造业生产工艺转型升级。
近来年,随着智能切割行业的高速发展,吸引了越来越多的企业发展智能切割行业相关产业,市场竞争加剧,会对企业自身的产品价格、毛利率、利润等产生不利影响。如果企业不能在日趋激烈的市场竞争中及时提高市场开发能力,无法精确把握相关领域技术应用的开发速度,将面临销售规模和盈利能力下降的风险。
地缘政治在对纺织鞋业智能切割设备行业造成多方面影响,包括贸易壁垒的提升、市场准入受限、抑制跨国投资与技术合作、促使企业重新评估供应链安全、政府推出政策导向与补贴措施,以及引发货币汇率波动,这些因素共同要求企业具备高度灵活性以适应快速变化的国际环境。
随着终端客户对产品个性化、定制化需求的不断提升,鞋履制造、服装纺织等行业的产品创新力度逐渐加强,设计理念、产品款式推陈出新速度快,因此不断出现的个性化产品使得生产工艺标准化下降,单纯的加工设备已无法应对产品生产工艺的快速变化与客户需求。
随着智能制造理念的日益成熟,震动刀加工设备逐步从单体加工设备向以震动刀加工为核心,集成其他功能部件的自动化智能加工产线转型,并结合机器视觉、在线检测等技术,实现智能生产。震动刀加工设备通过结合工业互联网技术与震动刀加工技术,实现生产计划管理、设备在线监控和维护、故障在线诊断等一系列功能的数字化设备,帮助生产企业提升效率、降低成本,未来震动刀+配套自动化设备的系统集成、智能化需求成为趋势。
随着客户对产品个性化、定制化需求的不断提升以及应用的深度挖掘,下游行业对产品设计、特殊工艺、多样化功能以及生产效率、精度等性能指标都提出了新的要求,生产工序也从单一工序的简单加工,演变成模块化、平台化、小批量、多品种的柔性生产,多种切割工艺并存且可灵活配置,智能切割设备也开始被运用于高精度切割等附加值较高的生产工序中。
伴随新材料出现,针对新材料的应用工艺开展研究,进行切割工艺突破,可以进入很多其他领域。如智能切割设备可以切割的材料从原来局限于布匹、纸张等柔性材料,逐渐向玻璃纤维、碳纤维、亚力克板、PVC、ETFE、PTFE、HAPALON 等新材料发展,进入新能源、航天航空材料、船舶材料、风电材料、光伏材料、医疗、建筑等多个新行业的切割工序中。
据恒州博智(QYR)调研团队最新报告“全球柔性鞋材振动刀智能视觉裁切机市场报告2024-2030”显示,预计2030年全球柔性鞋材振动刀智能视觉裁切机市场规模将达到1.6亿美元,未来几年年复合增长率CAGR为5.4%。
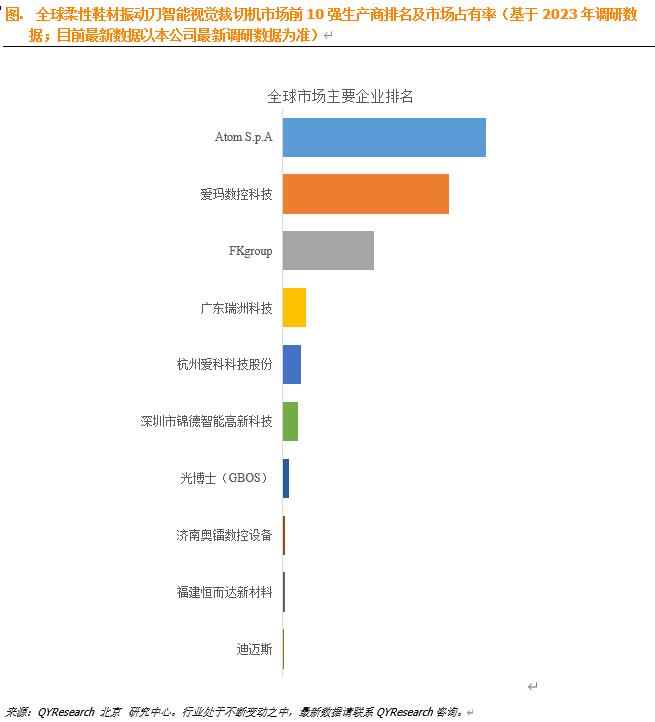
根据恒州博智(QYR)研究中心调研,全球范围内柔性鞋材振动刀智能视觉裁切机生产商主要包括Atom S.p.A、爱玛数控科技、FKgroup、广东瑞洲科技、杭州爱科科技股份等。2023年,全球前五大厂商占有大约87.0%的市场份额。
根据恒州博智(QYR)研究中心调研,全球范围内柔性鞋材振动刀智能视觉裁切机生产商主要包括Atom S.p.A、爱玛数控科技、FKgroup、广东瑞洲科技、杭州爱科科技股份、深圳市锦德智能高新科技、光博士(GBOS)、济南奥镭数控设备、福建恒而达新材料、迪迈斯等。2022年,全球前十强厂商占有大约92.0%的市场份额。
就产品类型而言,目前单龙头是最主要的细分产品,占据大约72.4%的份额。
就产品应用而言,目前大批量生产是最主要的需求来源,占据大约86.6%的份额。
