网站模块顺序调整html编辑器怎么用
文章目录
- 一、智慧物联案例分析
- 二、M2M技术
- 三、数据保护综合案例分析
一、智慧物联案例分析
智能物流是一种典型的物联网应用。一个物流仓储管理系统架构如下图所示:
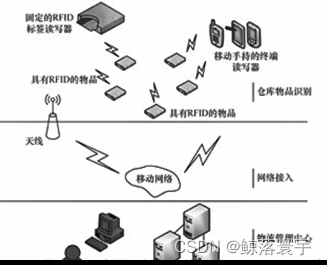
[问题1] 图中的三层功能:仓库物品识别、网络接入、物流管理中心,分别可对应到物联网基本架构中的哪一层?
[答案1]仓库物品识别功能对应于物联网的感知层;网络接入功能对应于物联网的传输层;物流管理中心功能对应于物联网的应用层
[问题2] 结合该图说明物联网三层架构各层的作用是什么? 所包含的主要技术有哪些?
[答案2]物联网的三层架构包括感知层、传输层和应用层。
感知层:其主要作用是实现物理世界信息的采集、自动识别和智能控制。涉及的技术包括传感器、RFID、二维码等数据采集技术,GPS定位技术等。本图中用到了RFID技术传输层:其主要作用是将感知层获取的各种不同信息传递到处理中心进行处理。
传输层:是基于既有的通信网络和互联网建立的,包括各种无线、有线网络,接入网,核心网。本图中用到了无线通信技术、移动通信网络.互联网技术
应用层:实现对采集到的数据的智能性处理。涉及的技术包括人工智能、中间件、云计算、大数据等技术,为不同行业提供应用解决方案。本图中用到了计算机软硬件、分布
