东莞网站开发方案关于网站开发的文献
注:本文为“圆与 π”相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
圆的历史:圆形几何图案在人类文明史中的演变轨迹与内涵
原创 遇见数学 2025年06月02日 10:30 河南
圆在史前文明中的出现
早在文字记录之前,人类就已经开始创造圆形结构。史前人类建造了巨大的石圆和木圆结构,英国的巨石阵就是最著名的例子之一。这些圆形结构可能与天文观测或宗教仪式有关。圆形元素在岩画和洞穴绘画中也很常见,显示了早期人类对这一完美形状的关注。

▲加利福尼亚州圣巴巴拉县的圆形洞穴壁画
考古发现的圆盘状史前文物包括内布拉星象盘(德国发现的青铜时代天文器具)和中国古代的玉璧。这些文物不仅是艺术品,也可能是早期天文或宗教物品。

▲内布拉星象盘,约 1800–1600 BC

▲战国时期双龙纹璧
圆在早期数学中的地位
圆的数学研究可以追溯到最早的文明。约公元前 1700 年的埃及莱因德纸草书提供了计算圆面积的方法。这个古老的数学文献使用了相当于将 π 值取为(约等于 3.16049…)的近似计算法。考虑到当时的技术条件,这已经是相当精确的近似值了。
莱因德纸草书是当前所知最具代表性的古埃及数学原始文献之一,由埃及抄写员阿赫梅斯(Ahmes)抄写。它不仅包含圆的计算,还有各种几何和代数问题的解法,展示了古埃及数学的高度发展。
古希腊数学家欧几里得在他的《几何原本》第三卷中系统地探讨了圆的性质。他对圆的严格定义奠定了几何学研究圆的基础:
圆是一个平面图形,由一条曲线所包围,并且从其内部的某一定点到这条包围线上任意点的所有直线都相等。这包围线被称为圆周,而那个点被称为圆心。-- 欧几里得,《几何原本》第一卷
这个定义精确地捕捉了圆的本质特征,至今仍被广泛使用。

▲ 画作《阿基米德之死》,据说阿基米德在被杀前所说 “别碰我的圆”。
柏拉图在《第七封信》中进一步深入探讨了圆的概念。他区分了理想中的完美圆与任何物理绘图或语言描述之间的差异,暗示了数学对象的抽象本质。这种思考反映了柏拉图的理念论哲学,认为真正的知识关注的是永恒不变的理念,而非感官世界中的具体实例。
圆与神圣观念的联系

古阿拉伯天文图画中的圆圈
在中世纪,科学(尤其是几何学、占星术和天文学)常与神学密切相关。许多学者认为圆形中蕴含着某种 “神圣” 或 “完美” 的品质。圆的完美对称性被视为上帝创造的象征,这也解释了为什么圆形在宗教艺术和建筑中如此普遍。
中世纪的哥特式教堂常常以巨大的玫瑰窗为特色,这些精美的圆形彩色玻璃窗不仅是建筑奇迹,也是数学与宗教结合的象征。它们通常采用复杂的几何图案,包含各种对称性和数学比例,被视为宇宙和神圣秩序的微缩表现。
圆的数学特性也持续吸引着学者们的研究。一个长期存在的几何问题是 “化圆为方”—— 即用有限步的直尺和圆规作图,构造一个与给定圆面积相等的正方形。这个问题困扰了数学家们数千年,直到 1880 年,德国数学家费迪南德・冯・林德曼最终证明了 π 是超越数,从而证明了这个问题在经典几何条件下无解。
现代艺术中的圆
进入 20 世纪,随着抽象艺术的兴起,几何形状本身成为了艺术表达的主题。俄罗斯艺术家瓦西里・康定斯基尤其喜欢在他的作品中使用圆形元素,将其视为表达宇宙和谐与精神维度的完美形式。

▲康定斯基《几个圆》,1926 年,纽约市所罗门・R・古根海姆博物馆
康定斯基在他 1926 年的作品《几个圆》中,展示了各种大小和颜色的圆漂浮在黑色背景上的构图。
圆的象征意义与宗教使用

▲对大多数中世纪学者来说, 科学 ,尤其是几何学和天文学 / 占星术 ,与神灵直接相关。这份 13 世纪手稿中的圆规象征着上帝的创世之举。上帝按照几何和谐律创造了宇宙,因此,寻求这些律则就是寻求和崇拜上帝
从人类最早的文明开始,圆就在视觉艺术中被用来传达各种思想和信息。不同文化对圆的理解和运用反映了其独特的世界观。例如亚述文明、古埃及文明、印度河流域文明和中国黄河流域文明,以及古典时期古希腊和古罗马等西方文明。
有些文化强调圆的周长,将其视为民主和平等的象征,因为圆周上的每一点都与中心等距。而其他文化则聚焦于圆心,将其视为宇宙统一和中心化权威的象征。

▲石刻法论
在神秘学说中,圆主要象征存在的无限和循环本质。衔尾蛇(一条吞食自己尾巴的蛇形成的圆)就是这种循环不息、永恒再生概念的经典表现。而在各种宗教传统中,圆形常代表天体和神圣精神。
圆承载了许多神圣和精神概念,包括统一、无限、完整、宇宙、神性、平衡、稳定和完美等。这些概念通过各种符号在全球文化中得到表达:圆规(创造的象征)、光环(神圣的标志)、鱼形符号及其衍生物、法轮、彩虹、曼荼罗和玫瑰窗等。

▲The Magic Circle by John William Waterhouse (1886)
在西方密传传统中,魔法圆被认为能创造一个神圣空间,保护施法者免受外界力量的干扰。这种观念在现代流行文化中仍有体现。
原内容及图片源自维基百科,遵循 CC BY-SA 4.0 协议。
原文:https://en.wikipedia.org/wiki/Circle#History
翻译:【遇见数学】译制,并补充部分内容 / 图片
π 的奇幻漂流:从祖冲之到超级计算机的 100 万亿位之旅
数学工作坊 2025年06月09日 10:01 上海
一根无限延伸的弦,串联起四大古文明的智慧结晶;
一串永不循环的数字,激荡着人类最疯狂的算力竞赛。
π 的故事,正是数学文明最壮丽的漂流史诗。

文明溯源
古埃及:金字塔里的数学智慧

古埃及工程师建造宏伟金字塔时,已经在实践中体现了对圆与方的独特理解。他们通过用正八边形逼近圆的方法来估算圆周率:将正八边形的每条边近似为圆的弧,便可以通过测量正八边形的周长来近似圆的周长。具体过程如下:
画一个逼近圆的正八边形,假设要逼近的圆直径为 d,计算出正八边形的周长 C 后根据 C=πd 计算 π 的近似值。莱茵德纸草书(公元前 1650 年)记载:用正八边形逼近圆时,圆周率 ≈ 3.1605。
古巴比伦:楔形文字中的数学密码
在古巴比伦的楔形文字泥板上,同样藏着圆周率的秘密。约公元前 1900 - 1600 年的一块泥板显示,他们使用 60 进制,将圆周率近似为 25/8,也就是 3.125。而在另一块年代稍晚的泥板上,同样出现了 3 + 1/8 ≈ 3.125 的近似值,展现出古巴比伦人高超的数学水平。
古印度:梵文古籍里的数学印记
在一些古老的梵文数学文献中,记载着他们对圆周长和直径关系的研究。公元 5 世纪,印度数学家阿耶波多在其著作《阿耶波多历算书》中,给出了圆周率的近似值,认为圆周率等于 62832/20000,即 3.1416 ,这一结果在当时处于世界领先水平,体现了古印度数学的独特魅力和深厚底蕴。
古代中国:算筹上的圆周率传奇

早在《周髀算经》中,就有 “周三径一” 的记载,简单认为圆周率约等于 3。到了汉代,数学家刘歆、张衡等不断钻研改进,让圆周率的计算更加精确,他们的努力为后世祖冲之算出领先世界近千年的圆周率数值奠定了坚实基础。
四大古文明 π 值对比


关键突破

公元 5 世纪,中国南北朝时期的伟大数学家祖冲之与其子祖暅,运用被称为 “缀术” 的方法(具体算法已失传,推测可能基于刘徽的 “割圆术”)将圆周率计算推进到空前绝后的精度:3.1415926 < π < 3.1415927。他不仅给出了约率 22/7,更发现了密率 355/113(这是分母小于 16604 的最佳分数近似),领先世界近千年。这需要难以想象的耐心与毅力,在算筹间进行千万次的开方、乘除迭代。
17 世纪,牛顿和莱布尼茨几乎同时发明了微积分,这为 π 的计算打开了全新的维度。
莱布尼茨公式:无穷级数的奇妙旅程
莱布尼茨公式是数学史上第一个用于计算圆周率 π 的无穷级数公式,它揭示了 π 与奇数序列之间的神秘联系。
π = 4 ( 1 − 1 3 + 1 5 − 1 7 + 1 9 − ⋯ ) \pi =4\left( 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots \right) π=4(1−31+51−71+91−⋯)
这个级数由德国数学家莱布尼茨在 17 世纪提出,虽然收敛速度较慢,但它开创了用无穷级数计算 π 的先河,展现了数学的无穷魅力。
马青公式:快速计算 π 的奇迹
马青公式是 18 世纪数学家约翰・马青发现的一个高效计算 π 的公式。它利用反正切函数的性质,将 π 表示为:
π = 16 arctan ( 1 5 ) − 4 arctan ( 1 239 ) \pi =16\arctan \left( \frac{1}{5} \right)-4\arctan \left( \frac{1}{239} \right) π=16arctan(51)−4arctan(2391)
马青成功计算出 π 的 100 位小数,这在当时是一个巨大的突破。马青公式不仅计算速度快,还为后续的 π 计算提供了重要思路。
反正切函数:连接几何与代数的桥梁
反正切函数 arctan (x) 是一个重要的数学函数,它表示角度的正切值为 x 的角度。在 π 的计算中,反正切函数扮演了关键角色。例如,马青公式正是基于反正切函数的性质,通过巧妙的组合和计算,实现了对 π 的高效逼近。反正切函数不仅连接了几何与代数,还为数学家们提供了探索 π 的强大工具。
从莱布尼茨的无穷级数到马青的高效公式,再到现代计算机算法,人类对 π 的探索从未停止。利用这些公式,数学家们可以系统地、理论化地逼近 π 值。π 的计算不再是单纯的几何测量,而是成为了分析数学的华丽舞台,精度开始飞跃式提升。
π 值计算里程碑

趣味应用
蒙特卡罗方法:基于随机抽样估算 π
蒙特卡罗法是一种基于随机抽样的计算方法,可用于估算圆周率 π。其原理是利用随机点在单位正方形内与单位圆内的分布比例来近似计算圆的面积。具体操作为:在单位正方形内随机生成大量点,统计其中落在单位圆内的点数与总点数的比例。由于单位圆的面积为 π,单位正方形的面积为 1,因此该比例应接近 π/4。通过:
π ≈ 4 × 圆内点数 总点数 \pi \approx 4\times \frac{圆内点数}{总点数} π≈4×总点数圆内点数
即可估算出圆周率。这种方法简单直观,且随着随机点数量的增加,估算结果会逐渐趋近于真实值。

大家可以准备一个正方形的纸板和一个内切的圆形纸板,再准备一袋小豆子。将圆形纸板放在正方形纸板的正中央,然后随机向正方形纸板内投掷豆子,记录落在圆形纸板内的豆子数量 I 和总豆子数量 A。根据蒙特卡罗法的原理,圆的面积与正方形面积的比值等于落在圆内的豆子数量与总豆子数量的比值。
即:
I A ≈ π 4 \frac{I}{A} \approx \frac{\pi}{4} AI≈4π
通过计算,我们可以得出圆周率的近似值:
π ≈ 4 × I A \pi \approx 4 \times\frac{I}{A} π≈4×AI
在看似随机的投掷中,隐藏着严谨的数学规律,这正是数学的魅力所在。
《圆周率之歌》
在数学与艺术的交汇处,总有一些奇妙的创意让人眼前一亮。作曲家大卫・麦克唐纳以 π 的前 31 位数字为音符(如 3 = M i , 1 = D o 3=M_i,1=D_o 3=Mi,1=Do),通过这样的转换,麦克唐纳将数学的严谨性与音乐的感性完美结合,创造出了一段空灵的旋律,即钢琴曲《圆周率之歌》。现在也有不少博主将 0-9 数字分别对应音符进行弹奏,让更多人感受到了数学与艺术结合的魅力:
从巴比伦泥板上的 60 进制分数,到瑞士机房中轰鸣的超级计算机;从祖冲之在算筹间刻画的千万次迭代,到记忆冠军脑海中奔流的数字长河 ——π 的奇幻漂流史,本质是人类对无限永恒的悲壮致敬。正如数学家迪尔曼所言:
“通过数学,自然在论述;通过数学,创造者在表达。”
END
撰稿丨施玟 万嘉婧
编辑丨万嘉婧 施玟
总责丨刘威娅 张颖
圆周率 π 的双重身份:无理数特性与正规性猜想全解读
原创 遇见数学 2025年05月31日 15:30 河南
无理性与正规性
π 是一个无理数(irrational number),这意味着它不能写成两个整数相除的形式。
虽然我们常用 22 7 \frac{22}{7} 722 和 355 113 \frac{355}{113} 113355 这样的分数来近似表示 π,但实际上没有任何一个分数能够精确等于 π 的值。

作为无理数,π 的小数部分永无止境,并且不会出现循环重复的模式。这与有理数形成鲜明对比 —— 所有有理数的小数部分最终都会进入循环。
证明 π 是无理数有多种方法,这些证明通常采用 “反证法”—— 假设 π 可以表示为分数,然后推导出矛盾,从而证明原假设错误。这些证明虽然需要一定的微积分知识,但核心思想并不复杂。
π 能被分数近似的难易程度(专业术语称为 “无理测度”,irrationality measure)是个有趣的问题。研究表明,π 的无理测度大于或至少等于自然对数底数 e,但小于 “刘维尔数”(Liouville numbers)。用通俗的话说,π 不太容易被简单分数精确近似,但也没有难到极端的地步。
无理测度可以类比为 “相机对焦的难度”:有些数字像清晰的风景,容易对焦(即用分数表示);而 π 则像是稍微模糊的对象,需要更精细的调整才能对焦清晰。刘维尔数则类似于极难对焦的烟雾,几乎无法用简单分数精确捕捉。
π 的数字序列展现出令人惊讶的随机性特征。它通过了各种统计随机性测试,包括检验它是否为 “正规数”(normal number)。一个正规数是指在其小数展开中,任何特定长度的数字组合出现的频率最终都相等。
简单来说,在一个十进制正规数中,每个数字 0-9 应各占约 10%,每个两位数组合(00-99)应各占约 1%,依此类推。
尽管有充分理由相信 π 是正规的,但这一猜想至今仍是一个开放问题 —— 既未被证明,也未被否定。这是数学中一个引人入胜的未解之谜。
计算机技术的进步使科学家能够计算 π 的万亿位小数,为统计分析提供了海量数据。日本数学家金田康正(Yasumasa Kanada)对 π 的小数部分进行了细致分析,结果支持 π 具有正规性的猜想。他检验了数字 0 到 9 的出现频率,发现它们分布均匀,没有偏好特定数字的迹象。

▲无限猴子定理指出,一只猴子在打字机键盘上独立且随机地敲击键盘,持续无限长的时间 ,几乎肯定会打出任何给定的文本,包括威廉・莎士比亚的全集。
根据 “无限猴子定理”(infinite monkey theorem),任何足够长的随机序列中必然会出现看似有规律的片段。这解释了为什么 π 的小数部分虽然整体随机,却能找到一些引人注目的模式。

▲π 的首一千个小数位(三位及更多相同数字连续出现的数字段已标出,内含六个 9)
最著名的例子是从 π 的小数点后第 762 位开始的连续六个 9(999999)。这个序列被数学爱好者亲切地称为 “费曼点”(Feynman point),因为据说著名物理学家理查德・费曼(Richard Feynman)曾开玩笑说他要把 π 背到这个位置,然后说 “九九九九九九,如此等等”,让人误以为此后 π 的小数点后全是 9。虽然这个轶事广为流传,但实际上没有确凿证据表明它与费曼有直接关系。
原内容及图片源自维基百科,遵循 CC BY-SA 4.0 协议。
原文:https://en.wikipedia.org/wiki/Pi#Fundamentals
翻译:【遇见数学】译制,并补充部分内容 / 图片
当圆周率遇见物理学:探索数学常数 π 如何参与塑造我们的物理世界观
原创 遇见数学 2025年05月29日 11:17 河南
在数学之外的应用:描述物理现象
虽然 π 不是像光速或普朗克常数那样的物理常数,但它经常出现在描述宇宙基本原理的方程中。这主要是因为 π 与圆和球面坐标系(spherical coordinate systems)有着内在联系,而自然界中许多现象都具有圆形或球形特性。
单摆
在经典力学领域中,描述简单摆的周期公式就包含 π。对于一个长度为 L L L、小幅度摆动的简单摆,其近似周期 T T T 可以表示为:
T ≈ 2 π L g T \approx 2\pi \sqrt{\frac{L}{g}} T≈2πgL
其中 g g g 是地球重力加速度。这个公式揭示了摆动周期与摆长的平方根成正比的关系。
遇见数学:这个公式解释了为什么长摆钟比短摆钟摆动得慢,这也是为什么古老的座钟通常都很高大——它们需要足够长的摆来获得精确的计时。
量子力学
量子力学的基石之一是海森堡不确定性原理(Heisenberg’s uncertainty principle),它表明我们无法同时精确测量粒子的位置( Δ x \Delta x Δx)和动量( Δ p \Delta p Δp):
Δ x Δ p ≥ h 4 π \Delta x \Delta p \geq \frac{h}{4\pi} ΔxΔp≥4πh
其中 h h h 是普朗克常数。这个原理揭示了微观世界的基本限制,也是量子力学与经典物理的本质区别。
粒子物理
π 近似等于 3 这一看似简单的事实,在粒子物理学中具有深远影响。例如,它影响了正电子偶素(正电子和电子形成的特殊束缚态)的寿命。以精细结构常数 α \alpha α 的最低阶表示的逆寿命为:
1 τ = 2 π 2 − 9 9 π m e α 6 , {\displaystyle {\frac {1}{\tau }}=2{\frac {\pi ^{2}-9}{9\pi }}m_{\text{e}}\alpha ^{6},} τ1=29ππ2−9meα6,
其中 m e m_e me 是电子质量。π 与 3 的微小差异在这里产生了重要影响。
结构工程
在结构工程中, π π π 出现在欧拉(Euler)推导的屈曲公式中。这个公式计算了细长柱体在不发生弯曲破坏的情况下能承受的最大轴向载荷:
F = π 2 E I L 2 F = \frac{\pi^2 E I}{L^2} F=L2π2EI
其中 L L L 是柱长, E E E 是弹性模量, I I I 是截面惯性矩。这个公式对于设计桥梁、建筑和各种承重结构至关重要。
遇见数学:这就解释了为什么高大的建筑物需要更粗的支柱——当高度( L L L)增加时,支撑能力( F F F)会按平方反比减小,必须通过增加截面积来补偿。
流体动力学
在流体动力学中,斯托克斯定律(Stokes’ law)描述了小球体在粘性流体中运动时受到的阻力,公式中也包含 π:
F = 6 π η R v . {\displaystyle F=6\pi \eta Rv.} F=6πηRv.
其中 F F F 是摩擦力, η \eta η 是流体动态粘度, R R R 是球体半径, v v v 是运动速度。这个定律解释了从雨滴下落到血细胞在血管中流动的各种现象。
电磁学
在电磁学领域,麦克斯韦方程(Maxwell’s equations)中的真空磁导率常数 μ 0 \mu_0 μ0 包含 π π π。在 2019 年 5 月 20 日国际单位制重新定义之前,它被精确定义为:
μ 0 = 4 π × 10 − 7 H/m ≈ 1.2566370614 × 10 − 6 N/A 2 \mu_0 = 4\pi \times 10^{-7} \, \text{H/m} \approx 1.2566370614 \times 10^{-6} \, \text{N/A}^2 μ0=4π×10−7H/m≈1.2566370614×10−6N/A2
这个常数连接了电流和磁场,是电磁理论的核心参数。
原内容及图片源自维基百科,遵循 CC BY-SA 4.0 协议。
原文:https://en.wikipedia.org/wiki/Pi#Outside_mathematics
翻译:【遇见数学】译制,并补充部分内容 / 图片
复数与欧拉恒等式:π 如何在复平面上展现数学之美?
原创 遇见数学 2025年06月05日 11:16 河南
复数的极坐标表示
在复数世界中,任何复数 z z z 都可以用两个实数来表示:
z = a + b i z = a + b i z=a+bi
而在极坐标系统中,我们用另一种更直观的方式表示:
z = r ⋅ ( cos φ + i sin φ ) z = r \cdot ( \cos \varphi + i \sin \varphi ) z=r⋅(cosφ+isinφ)
这里:
- r r r 是模(radius):表示复数 z z z 在复平面上距离原点的距离。
- φ \varphi φ 是辐角(angle):表示从正实轴逆时针旋转到达点 z z z 所需的角度。
- i i i 是虚数单位:满足 i 2 = − 1 i^{2} = -1 i2=−1。
直观的几何解释:想象复平面上有一个从原点出发的射线,长度为 r r r,与正实轴的夹角为 φ \varphi φ。这个射线的终点就代表复数 z z z。
例如,复数 3 + 4 i 3 + 4i 3+4i 可以用极坐标表示为 5 e i arctan ( 4 / 3 ) 5 e^{i \arctan (4 / 3)} 5eiarctan(4/3),其中 r = 5 r = 5 r=5(因为 3 2 + 4 2 = 5 \sqrt{3^{2} + 4^{2}} = 5 32+42=5),而 φ = arctan ( 4 / 3 ) \varphi = \arctan (4 / 3) φ=arctan(4/3),约为 0.927 0.927 0.927 弧度或 53.13 53.13 53.13 度。
欧拉公式:连接指数与三角函数
在复分析中,π 频繁出现的原因与复变量指数函数的行为密切相关,这可以通过著名的欧拉公式(Euler’s formula)来理解:
e i φ = cos φ + i sin φ e^{i \varphi} = \cos \varphi + i \sin \varphi eiφ=cosφ+isinφ
这里的常数 e e e 是自然对数的底(约等于 2.71828 2.71828 2.71828)。这个优雅的公式建立了 e e e 的虚数幂与复平面中以原点为中心的单位圆上点之间的精确对应关系。

▲ 复平面上所示的欧拉公式
欧拉公式说明指数函数和三角函数之间令人惊讶的关系,当我们计算 e e e 的纯虚数幂时,结果是落在复平面的单位圆上的复数,其实部是角度 φ \varphi φ 的余弦值,虚部是角度 φ \varphi φ 的正弦值。例如:
- e i ⋅ 0 = 1 e^{i \cdot 0} = 1 ei⋅0=1(单位圆与正实轴的交点
- e i ⋅ π / 2 = i e^{i \cdot \pi / 2} = i ei⋅π/2=i(单位圆与正虚轴的交点)
- e i ⋅ π = − 1 e^{i \cdot \pi} = -1 ei⋅π=−1(单位圆与负实轴的交点)
这就像是在单位圆上绕行,角度 φ \varphi φ 决定了行进的距离。
欧拉恒等式:五个常数的完美融合
当我们在欧拉公式中设定 φ = π \varphi = \pi φ=π 时,就得到了令数学家们赞叹不已的欧拉恒等式(Euler’s identity):
e i π + 1 = 0 e^{i \pi} + 1 = 0 eiπ+1=0
这个简洁的等式之所以备受推崇,是因为它神奇地将数学中五个最重要的常数—— 0 0 0、 1 1 1、 π \pi π、 e e e 和 i i i,以及三种基本运算:加法、乘法和指数运算——联系在了一个简单而深刻的关系中。
欧拉恒等式常被称为“数学中最美丽的公式”。它将代数中的 1 1 1 和 0 0 0、自然常数 e e e、圆周率 π \pi π 和虚数单位 i i i 完美结合,展现了数学内在的和谐与统一。物理学家理查德·费曼曾称它为“我们的珠宝”,而数学家本杰明·皮尔斯则形容它为“绝对天才之作”。
单位根:复数的周期性
欧拉公式还帮助我们理解“单位根”的概念。在复数理论中,方程 z n = 1 z^{n} = 1 zn=1 有 n n n 个不同的复数解,这些解被称为“单位根”( n n n-th roots of unity)。它们可以通过以下优雅的公式表示:
e 2 π i k / n ( k = 0 , 1 , 2 , … , n − 1 ) e^{2 \pi i k / n} \quad ( k = 0, 1, 2, \dots, n - 1 ) e2πik/n(k=0,1,2,…,n−1)

▲复平面上的三次单位根
单位根在复平面上形成一个正 n n n 边形,均匀分布在单位圆上。例如:
- 当 n = 3 n = 3 n=3 时,三个单位根是 1 1 1、 e 2 π i / 3 e^{2 \pi i / 3} e2πi/3、 e 4 π i / 3 e^{4 \pi i / 3} e4πi/3,它们在单位圆上形成一个正三角形。
- 当 n = 4 n = 4 n=4 时,四个单位根是 1 1 1、 i i i、 − 1 -1 −1、 − i -i −i,它们在复平面上形成一个正方形,分别位于实轴和虚轴上。
单位根在信号处理、数论和代数几何中有重要应用,特别是在快速傅里叶变换算法中发挥着核心作用。
版权声明:CC BY - SA 4.0
参考来源:https://en.wikipedia.org/wiki/Pi#Complex_numbers_and_Euler’s_identity
圆周率不只是无理数:探秘 π 的超越性与 “化圆为方” 不可能的数学奥秘
原创 遇见数学 2025年06月03日 11:17 河南
圆周率的超越性:超越代数方程的神奇常数
超越数的奇妙性质
圆周率 π 不仅是一个无理数(不能表示为两个整数的比值),它还拥有更深层次的神秘特性 —— 它是一个超越数(transcendental number)。
什么是超越数?简单来说,超越数是那些不能成为任何非零有理系数多项式方程的解的数。例如,π 不可能是下面这样的方程的解:
这个重要性质是由林德曼 - 威尔施特拉斯定理(Lindemann–Weierstrass theorem)证明的。这个定理同时也证明了自然对数的底数 e 也是超越数。

超越数的概念最早由欧拉在 1744 年提出,但直到 1844 年才由法国数学家约瑟夫・刘维尔(Joseph Liouville)首次证明超越数的存在。随后在 1882 年,德国数学家林德曼证明了 π 的超越性,解决了古希腊以来的 “化圆为方” 问题。

超越性带来的重要结论
π 的超越性质导致了两个极其重要的结论:
首先,π 不能用任何有限组合的有理数和平方根或 n 次方根来精确表达。也就是说,不存在像 2 \sqrt{2} 2 或 5 3 \sqrt[3]{5} 35 这样的根式组合能够精确等于 π。这解释了为什么我们只能用无限小数或无限级数来逼近 π 的值。
其次,由于超越数无法通过尺规作图法构造(只用直尺和圆规),因此古老的 “化圆为方” 问题被证明是不可能完成的。换句话说,不可能仅使用圆规和直尺,构造出一个面积恰好等于给定圆面积的正方形。
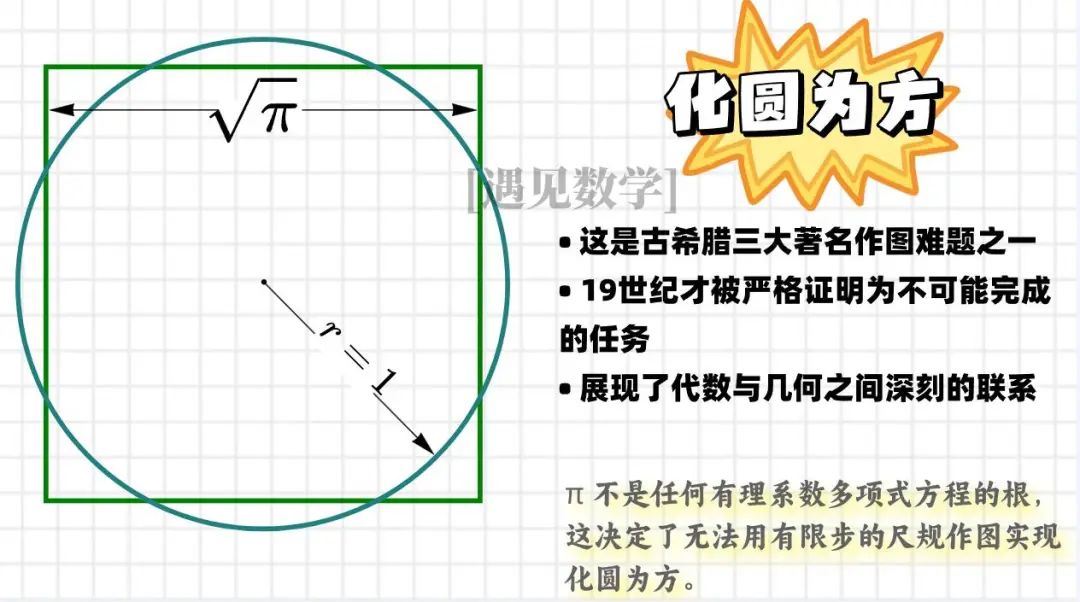
尺规作图只能构造有理数和可以由有理数通过有限次加减乘除和开平方根得到的数。这样的数被称为规矩数 (constructible number)。由于 π 是超越数,它不是尺规数,因此无法通过尺规作图精确构造长度为 π 的线段,这直接导致了 “化圆为方” 问题的不可解性。
“化圆为方” 的历史意义
“化圆为方”(squaring the circle)是古典几何学中最著名的三大作图难题之一(另外两个是三等分角和倍立方体)。这个问题可以追溯到古希腊时期,曾吸引了无数数学家尝试解决。
尽管现代数学已经严格证明这个问题在尺规作图下是不可能的,但仍有一些业余数学爱好者声称找到了解决方案 —— 这些声称从数学上来说是不成立的,因为它们违背了 π 的超越性这一基本性质。
数学前沿的未解之谜
在现代数学中,关于 π 的一个重要未解决问题是:π 和 e(自然对数的底数)是否代数独立(algebraic independence),也称为 “相对超越”(relatively transcendental)。简单来说,这个问题询问:π 和 e 之间是否存在某种非平凡的代数关系?
这个问题能够由尚未被证明的沙努埃尔猜想(Schanuel’s conjecture)解决 —— 该猜想是林德曼 - 威尔施特拉斯定理的一个广泛推广,涉及到超越数理论的深层问题。
如果两个超越数是代数独立的,那么它们的任意有理系数多项式组合(至少有一个系数非零)也都是超越数。目前已知 π 和 e 各自是超越数,但还不知道像 π+e 或 πe 这样的组合是否是超越数。
原内容及图片源自维基百科,遵循 CC BY-SA 4.0 协议。
原文:https://en.wikipedia.org/wiki/Pi#Transcendence
翻译:【遇见数学】译制,并补充部分内容 / 图片
圆周率 π 不止一种定义:从直观几何到抽象代数,多视角解读这个数学常数
原创 遇见数学 2025年06月04日 11:17 河南
π 的多种定义方式
圆周率 π 是数学中最基本的常数之一。看下面简单的圆形图,我们能看到标注的直径(diameter)和周长(circumference)。

最直观的定义是将 π π π 视为圆周长与直径的比值:
π = C d π = \frac{C}{d} π=dC
这个比值 C d \frac{C}{d} dC 是恒定的,与圆的大小无关。无论圆有多大或多小,这个比值始终不变。例如,如果一个圆的直径是另一个圆的两倍,那么它的周长也恰好是另一个圆的两倍,从而保持比值 C d \frac{C}{d} dC 不变。
想象一个直径为 2 厘米的小圆和一个直径为 20 厘米的大圆。小圆周长约为 6.28 厘米,大圆周长约为 62.8 厘米。虽然大小相差 10 倍,但 “周长 ÷ 直径” 的结果都是 π!
这种 π 的定义基于平面(欧几里得)几何;虽然圆的概念可以扩展到曲面(如球面)几何中,但在那些空间里的 “圆” 将不再满足公式 π = C d π = \frac{C}{d} π=dC。
圆的周长指的是围绕圆周的弧长,这个量可以使用微积分中的极限概念严格定义。例如,我们可以直接计算单位圆(半径为 1 的圆)上半部分的弧长,这个单位圆由方程 x 2 + y 2 = 1 x^2 + y^2 = 1 x2+y2=1 表示,通过积分可得:
π = ∫ − 1 1 d x 1 − x 2 \pi = \int_{-1}^{1} \frac{dx}{\sqrt{1 - x^2}} π=∫−111−x2dx
这个积分计算的是从点 (-1,0) 到点 (1,0) 沿单位圆上半部分的弧长,结果恰好等于 π。这展示了 π 不仅是几何概念,也可以通过纯数学分析方法定义。
这样的积分是由卡尔・魏尔斯特拉斯(Karl Weierstrass)在 1841 年提出作为 π 的定义,他直接将其定义为一个积分。不过在大学数学课程安排中,积分学这一部分通常安排靠后。
雷默特(Remmert)在 2012 年的著作中解释了这一点:如果定义 π 需要用到积分,那么学生在学习微分学时就无法严格理解 π,这不符合教学顺序。因此,数学家们希望找到一个不依赖积分的 π 定义。
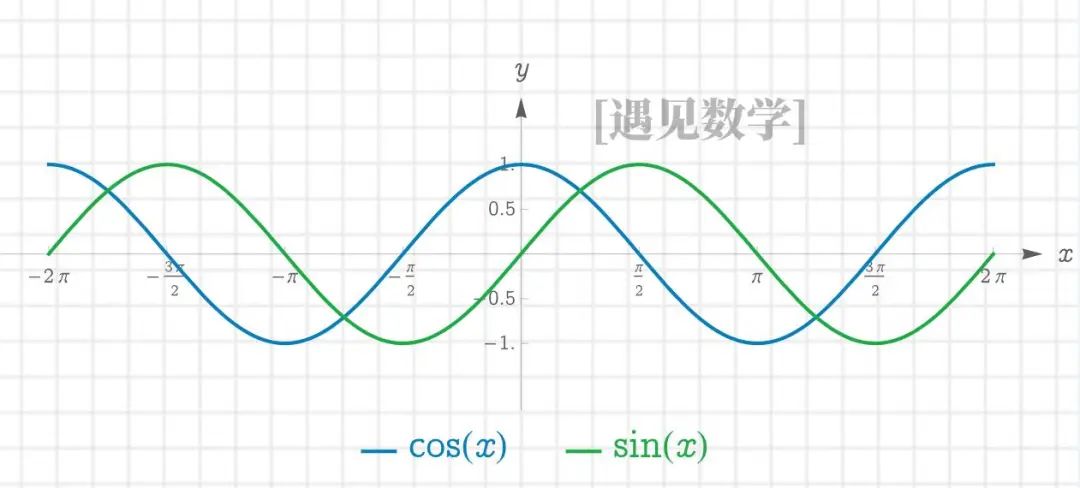
π 的第二种重要定义来自三角函数。数学家理查德・巴尔策尔(Richard Baltzer)提出并被埃德蒙・兰道(Edmund Landau)推广的定义是:
π 是余弦函数等于 0 的最小正数的两倍
这个定义非常巧妙,因为不需要用到积分;它与几何直觉相符(在单位圆上,从 (1,0) 走到 (0,1) 时的角度是 π 2 \frac{\pi}{2} 2π,此时余弦值为 0);可以在纯分析的框架内理解。
同样地,π 也可以定义为:
- 使正弦函数等于 0 的最小正数(即 π 本身)
- 正弦函数连续零点之间的差值(正弦函数在 0 , π , 2 π 0, π, 2π 0,π,2π 等点处等于 0)
重要的是,现代数学可以完全独立于几何来定义余弦和正弦函数,例如通过幂级数或微分方程。
π 的第三种定义来自复分析。π 可以使用复指数函数 e z e^{z} ez 的性质来定义,其中 z z z 是一个复数。
当我们寻找满足 e z = 1 e^{z} = 1 ez=1 的所有复数 z z z 时,它们形成了一个等差数列:
{ ⋯ , − 4 π i , − 2 π i , 0 , 2 π i , 4 π i , ⋯ } = { 2 π k i ∣ k ∈ Z } \left\{ \cdots ,-4\pi i,-2\pi i,0,2\pi i,4\pi i,\cdots \right\}=\left\{ 2\pi ki|k\in \mathbb{Z} \right\} {⋯,−4πi,−2πi,0,2πi,4πi,⋯}={2πki∣k∈Z}
这个序列中的数相隔 2 π i 2πi 2πi,而 π 就是使这个规律成立的唯一正实数。这个定义连接了 π 与自然对数的底 e e e,展示了数学中深刻的内在联系。
当我们在复平面上以原点为中心转一整圈(角度为 2 π 2π 2π)时, e i θ e^{i\theta} eiθ 正好完成一个完整循环回到起点 1。这个让函数回到起点所需的角度的一半,就是 π。这个定义本质上是在说:π 与复平面上的周期性密切相关。其实和第四种定义表达同一件事:π 是复平面上基本周期单位的一半。
还有更抽象的第四种定义,涉及拓扑学和代数学概念:π 可以定义为从 “圆周群”(实数模整数 R / Z \mathbb{R}/\mathbb{Z} R/Z,可以想象为把直线卷成圆)到复平面单位圆的自然同构映射 f ( t ) = e 2 π i t f(t) = e^{2πit} f(t)=e2πit 的导数大小的一半。
简单说,π 是连接两种不同表示 “圆” 方法的桥梁。一种方法用 0 到 1 之间的实数表示圆周上的位置(超过 1 就又回到起点),另一种用复平面上的单位圆表示。当位置值增加 1 个完整周期时,对应复数的变化速率正好是 2 π 2π 2π。这个关系显示了 π 在数学结构中的核心地位:它是使圆周运动在不同数学体系中完美对应的那个关键常数。
原内容及图片源自维基百科,遵循 CC BY-SA 4.0 协议。
原文:Pi - Wikipedia
翻译:【遇见数学】译制,并补充部分内容 / 图片
弹性碰撞次数与 π 的关联
欣泽物理解题研究 2023年01月15日 08:00 山东



一道弹性碰撞的物理题,结果为什么会出现 π?
王赟 遇见数学 2025年05月30日 11:16 河南
来源 | 《你没想到的数学》
作者 | 王赟
第一次波折:争议与批评
有这样一道有趣的物理题,出现在 “3Blue1Brown”“李永乐老师” 等许多在线视频中。
如图 1.1 所示,光滑的地面上放着大小两个滑块,左边是墙。大滑块的质量是小滑块的 n 倍。给大滑块一个向左的初速度,两个滑块之间及小滑块与墙之间会发生多次碰撞。假设碰撞没有能量损失,问一共会发生多少次碰撞?
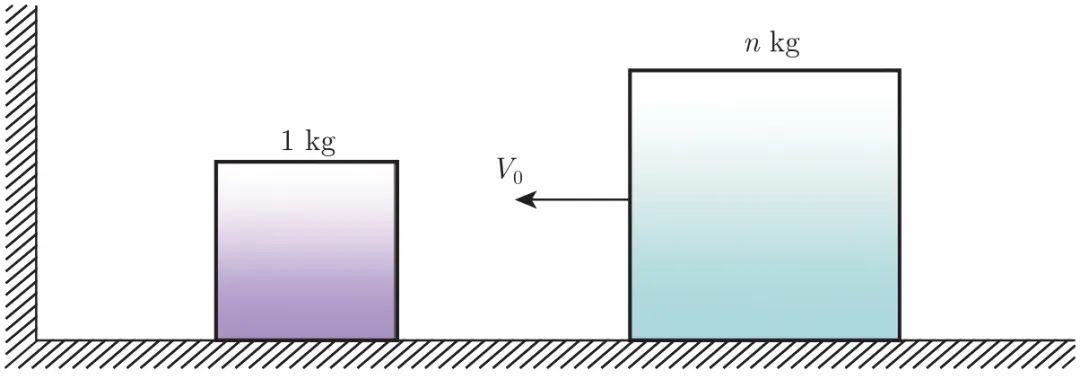
图 1.1 两个小滑块
在初步接触该物理问题时,可能会认为这是一道常规的力学习题而忽视其深层内涵。事实上,当对系统参数进行量化分析后,可观察到碰撞次数与质量比之间存在规律性关联。以下为不同质量比条件下的碰撞次数统计:
- 当两滑块质量相等(即质量比 n = 1 n = 1 n=1)时,系统共发生 3 次碰撞;
- 当大滑块质量为小滑块的 100 倍( n = 10 2 n = 10^2 n=102)时,碰撞次数为 31 次;
- 当质量比为 n = 10 4 n = 10^4 n=104(即 1 万倍)时,碰撞次数增至 314 次;
- 质量比 n = 10 6 n = 10^6 n=106(1 百万倍)时,碰撞次数为 3141 次;
- 质量比 n = 10 8 n = 10^8 n=108(1 亿倍)时,碰撞次数达到 31415 次。
上述数据呈现出显著的规律性:当质量比为 100 k 100^k 100k(100 的幂时,即 10 2 k 10^{2k} 102k)时,碰撞次数序列恰好对应圆周率 π \pi π 去掉小数点后的前 k + 1 k + 1 k+1 位数字(如 π = 3.1415926 ⋯ \pi = 3.1415926\cdots π=3.1415926⋯)。这一现象引发思考:在看似纯力学的“线性-碰撞”系统中,为何会出现与圆几何相关的常数 π \pi π?该问题的特殊性在于打破了几何图形与物理过程的表观界限,揭示了不同学科领域内在的数学统一性。
“3Blue1Brown” 频道给出了一个提示:凡是出人意料地出现 π 的题目,背后总是隐藏着一个圆。而这道物理题里的圆,隐藏在能量守恒方程式中:
1 2 m v 2 + 1 2 M V 2 = 常数 (1.1) \frac {1}{2} m v^{2}+\frac {1}{2} M V^{2}= 常数 \tag{1.1} 21mv2+21MV2=常数(1.1)
其中, M M M 和 m m m 分别表示大滑块与小滑块的质量, V V V 和 v v v 分别表示大滑块与小滑块的速度。建议读者在继续阅读之前,先基于式(1.1)进行自主推导,探究能否推导出圆周率 π \pi π 的相关表达。
隐藏的椭圆
式 (1.1) 实际上表示了 v − V v-V v−V 空间中的一个椭圆。设大滑块的初速度为 - 1 (负号代表向左),则能量守恒方程式可以化简为:
v 2 n + V 2 = 1 (1.2) \frac {v^{2}}{n}+V^{2}=1 \tag{1.2} nv2+V2=1(1.2)
这个方程式表示的椭圆如图 1.2 所示 (图中取 n = 4 n=4 n=4 )。在运动过程中的任何时刻,两个滑块的速度都会落在椭圆上;两个滑块的初速度,对应着短轴的下端 (图中 A 点)。
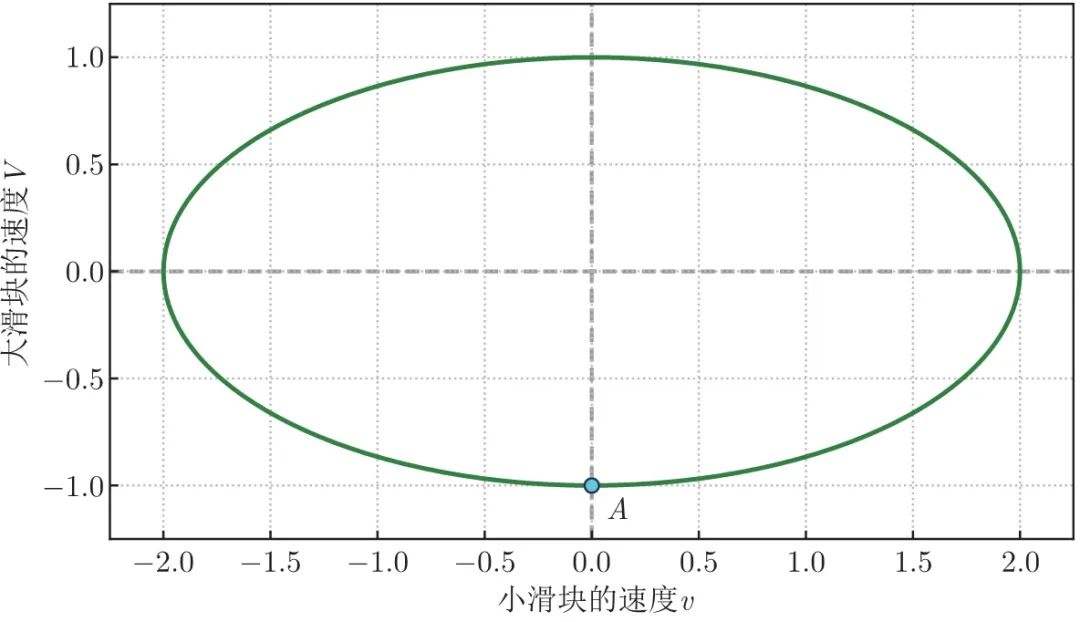
图 1.2 椭圆代表能量守恒
下面我们试着在椭圆中画出碰撞过程。第一次碰撞,是大滑块撞小滑块。碰撞前后,两个滑块的速度除了满足能量守恒以外,还要满足动量守恒,即:
m v + M V = 常数 (1.3) m v+M V = 常数 \tag{1.3} mv+MV=常数(1.3)
式 (1.3) 在 v − V v-V v−V 空间中,代表一条斜率为 − m / M -m/M −m/M 的直线,这个例子中的斜率为 − 1 / n -1/n −1/n 。如图 1.3,过 A 点作一条斜率为 − 1 / n -1/n −1/n 的直线,它与椭圆的另一个交点 B 就代表了第一次碰撞后,两个滑块的速度。
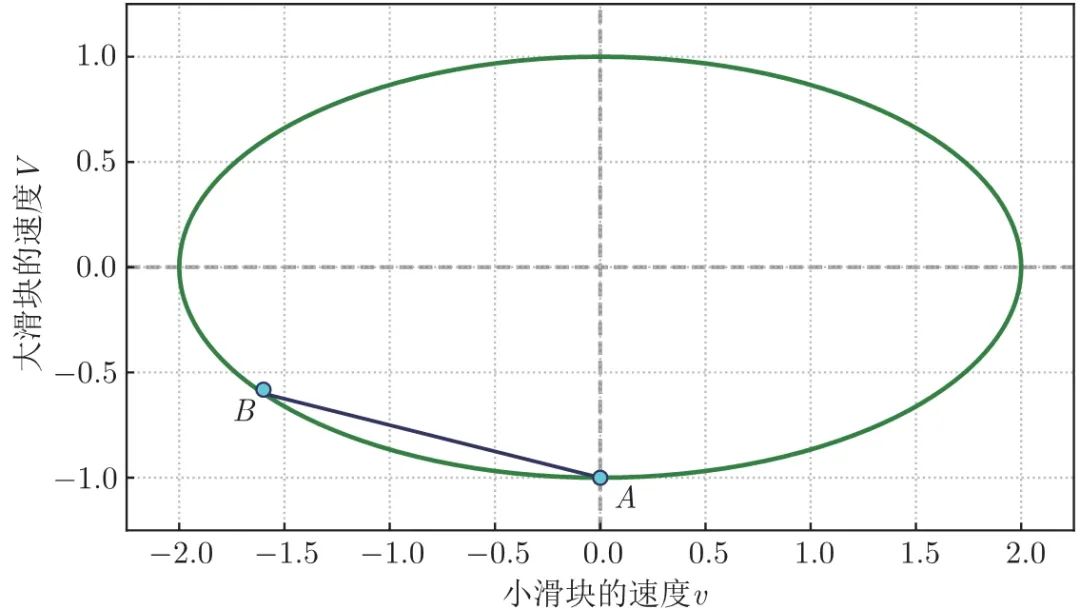
图 1.3 倾斜直线代表两个滑块相撞时动量守恒
第二次碰撞,是小滑块撞墙。其结果很简单,就是小滑块的速度变为反向。如图 1.4,过 B 点画一条与横轴平行的直线,这条直线与椭圆的交点 C 就代表了第二次碰撞后两个滑块的速度。

图 1.4 水平直线代表小滑块与墙碰撞
重复上述过程,直到 V ≥ v ≥ 0 V ≥v ≥0 V≥v≥0 。此时,两个滑块都向右运动,但小滑块追不上大滑块了,于是不会再发生碰撞。在 v − V v-V v−V 空间中,代表两个滑块最终速度的点一定会位于第一象限中直线 V = v V=v V=v 上方 (图中的黄色区域),这个例子中是图 1.5 中的 G 点。
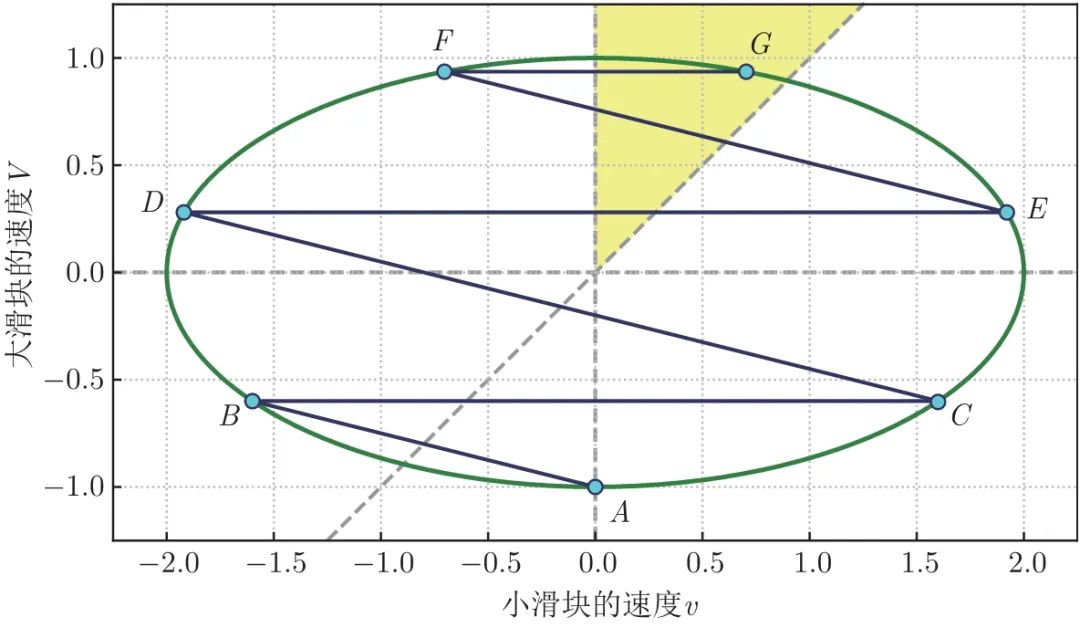
图 1.5 v − V v-V v−V 空间中的整个碰撞过程
可以注意到图 1.5 中弧 A C 、 B D 、 C E 、 D F 、 E G A C、B D、C E、D F、E G AC、BD、CE、DF、EG 所对的 “椭圆周角”(角 B、C、D、E、F) 都是相等的,等于 θ。弧 A B A B AB 与 A C A C AC 对称,也可以让它对应 “椭圆周角” A C B A C B ACB ,这个角也等于 arctan ( 1 / n ) \arctan (1 /n) arctan(1/n) 。联想到圆中有 “等弧所对圆周角相等” 的性质,而椭圆中没有,于是想到如果把椭圆 “捏” 成圆,会不会有意外发现?
将图 1.5 整体在横向上压缩到原来的 1 / n 1/\sqrt {n} 1/n 倍,则椭圆就变成了单位圆,如图 1.6 所示。
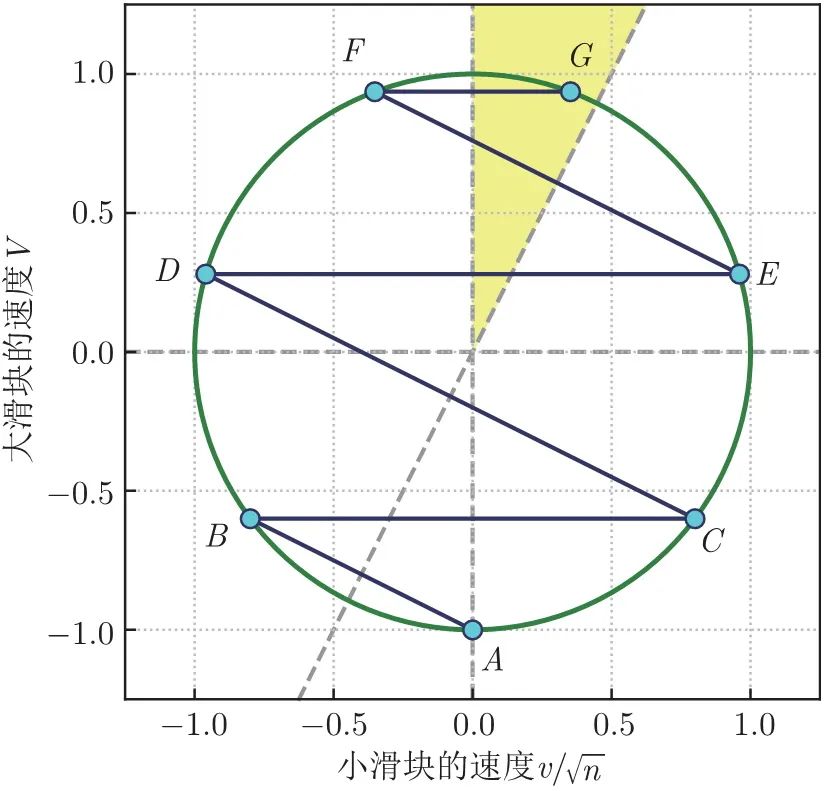
图 1.6 把椭圆 “捏” 成单位圆
这样一压缩,线段 A B 、 C D 、 E F A B、C D、E F AB、CD、EF 的斜率就都从 − 1 / n -1/n −1/n 变成了 − 1 / n -1/\sqrt {n} −1/n ,各段圆弧 (除了 F G F G FG ) 所对的圆周角也都变成了 arctan ( 1 / n ) \arctan (1 / \sqrt {n}) arctan(1/n) 。现在可以利用 “等弧所对圆周角相等” 了 —— 这些圆弧的长度,都等于这个圆周角的 2 倍,即 2 arctan ( 1 / n ) 2 \arctan (1 / \sqrt {n}) 2arctan(1/n) 。滑块的碰撞,可以看成从单位圆上不断切下一段长度为 2 arctan ( 1 / n ) 2\arctan (1 / \sqrt {n}) 2arctan(1/n) 的圆弧,直到剩余部分长度不超过 2 arctan ( 1 / n ) 2 \arctan (1 / \sqrt {n}) 2arctan(1/n) 为止。而整个单位圆的周长是 2 π 2 \pi 2π (注意 π 出现了!),于是可以得到总的碰撞次数:
⌈ 2 π 2 arctan ( 1 / n ) ⌉ − 1 (1.4) \left\lceil\frac {2 \pi}{2 \arctan (1 / \sqrt {n})}\right\rceil-1 \tag{1.4} ⌈2arctan(1/n)2π⌉−1(1.4)
这里的取整符号看起来较复杂,实际想要达到的效果是,一般情况 (不能整除时) 向下取整,特殊情况 (能整除时) 取商再减一。请读者自行验证。
由式 (1.4) 可以算出,当两个滑块质量相等时, arctan ( 1 / n ) = π / 4 \arctan (1 / \sqrt {n})=\pi / 4 arctan(1/n)=π/4 ,碰撞总次数为 3。而当两个滑块质量悬殊时, 1 / n 1/\sqrt {n} 1/n 会很小,此时 arctan ( 1 / n ) \arctan (1 / \sqrt {n}) arctan(1/n) 可以直接用 1 / n 1/ \sqrt {n} 1/n 来近似表示,于是碰撞总次数约为 ⌊ n π ⌋ \lfloor\sqrt {n} \pi\rfloor ⌊nπ⌋ 。当两个滑块的质量之比 n 是 100 的幂时, n \sqrt {n} n 就是 10 的幂,这就解释了碰撞总次数为什么会恰好是 π π π 去掉小数点后的前若干位。
via:
- 圆的历史:揭秘圆形几何图案在人类文明史中的演变轨迹与内涵
https://mp.weixin.qq.com/s/qJMBfgKdlF6zQVzPTBi5Lg - 圆周率 π 的双重身份:无理数特性与正规性猜想全解读
https://mp.weixin.qq.com/s/vQTVlzhCTy5e1M89aww8uQ - 当圆周率遇见物理学:探索数学常数 π 如何参与塑造我们的物理世界观
https://mp.weixin.qq.com/s/35ObBSw_GrkWBN9_XrCMMg - 【学数学】π 的奇幻漂流
https://mp.weixin.qq.com/s/00RfSvJMajQf2WO2kkkCEg - 复数与欧拉恒等式:π 如何在复平面上展现数学之美?
https://mp.weixin.qq.com/s/2glEaDPEH0HFCRJ7Eomlwg - 圆周率不只是无理数:探秘 π 的超越性与 “化圆为方” 不可能的数学奥秘
https://mp.weixin.qq.com/s/eQDu0hMBvZnAL5vwWVWYyw - 圆周率 π 不止一种定义:从直观几何到抽象代数,多视角解读这个数学常数
https://mp.weixin.qq.com/s/4UtMFjYrqGcY51tfoHampQ - 弹性碰撞次数与 π 的关联
https://mp.weixin.qq.com/s/SurK3L20yiAKwds2n3X4Fw - 一道弹性碰撞的物理题,结果为什么会出现 π?
https://mp.weixin.qq.com/s/eyspKHx23Igs3ra2hN-baA
