上海网站建设费用多少微信小程序怎么删除
御风以翔
破浪以飏
🎥个人主页
🔥个人专栏
目录
点亮一盏LED灯
LED的组成原理
LED的硬件模型
点亮一盏LED灯的程序设计
LED灯闪烁
LED流水灯
独立按键控制LED灯亮灭
独立按键的组成原理
独立按键的硬件模型
独立按键控制LED灯状态
按键的抖动
独立按键控制LED灯移位
位移的原理
点亮一盏LED灯
LED的组成原理
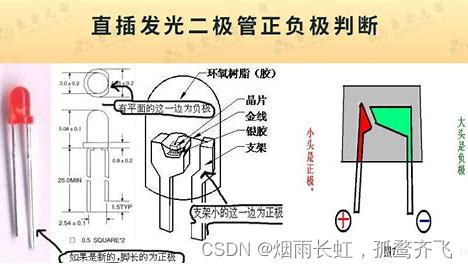
<1>LED即发光二极管,是一种有方向性的半导体固体发光器件,在单片机上是贴片形式
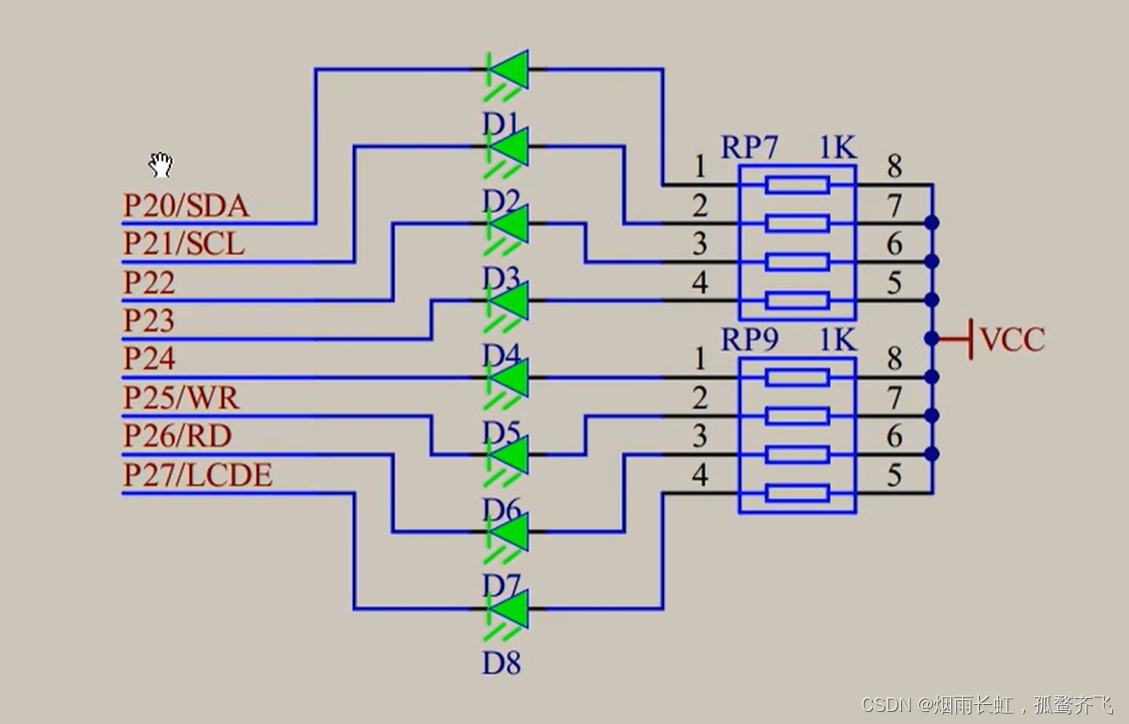
<2>LED的 阳极 串联一个电阻,然后连接到电源VCC,而LED的 阴极 连接到单片机的P2口,如果想把LED灯点亮,就把单片机相关的 I/O 口赋为低电平
<3>单片机中,用 0 表示低电频,用 1 表示高电频
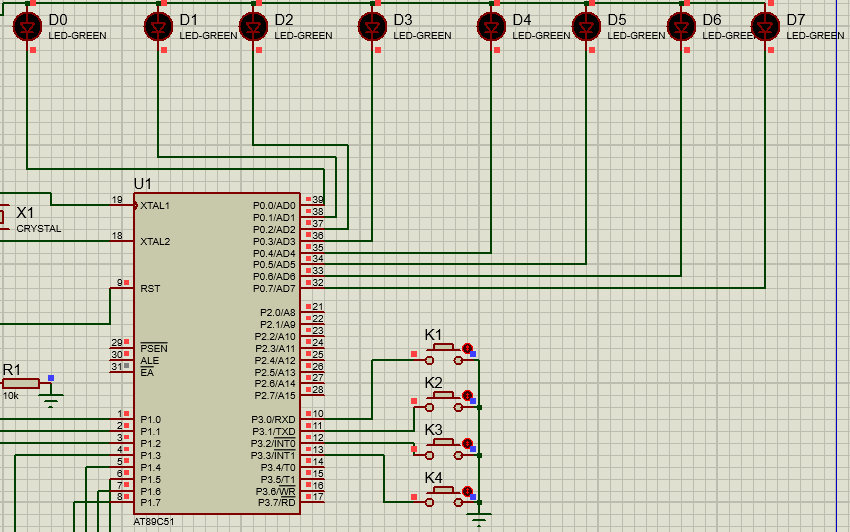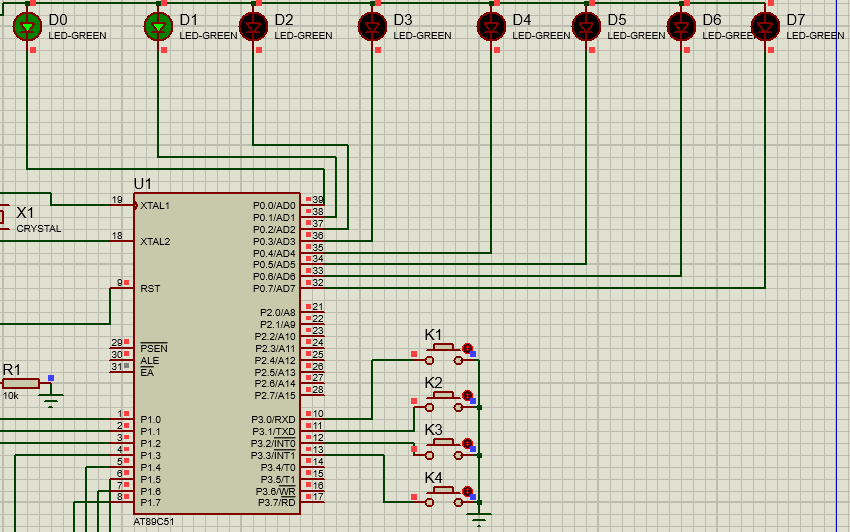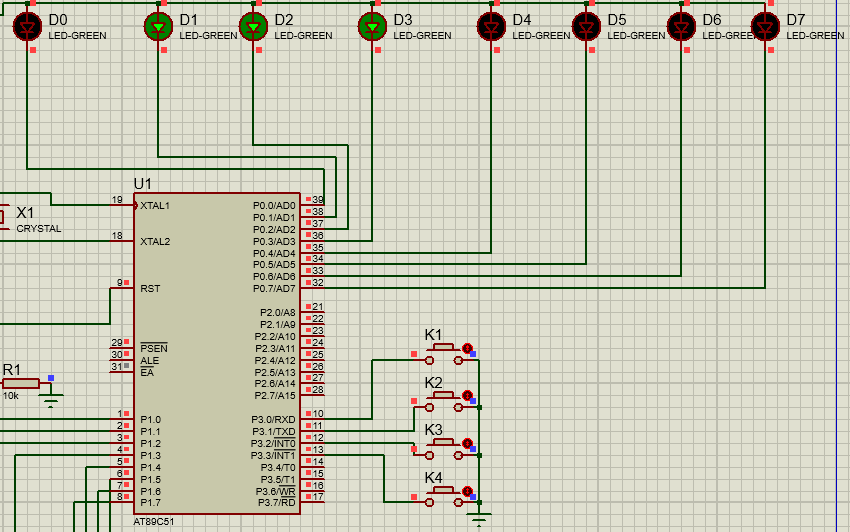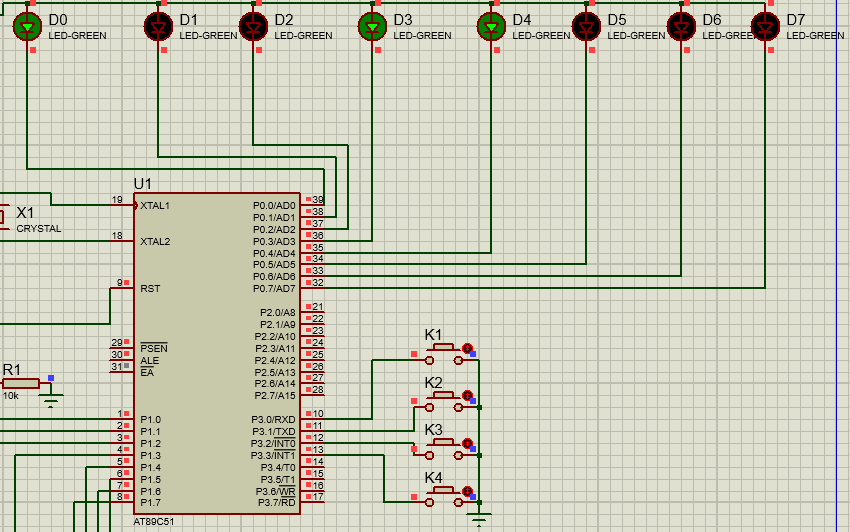
LED的硬件模型
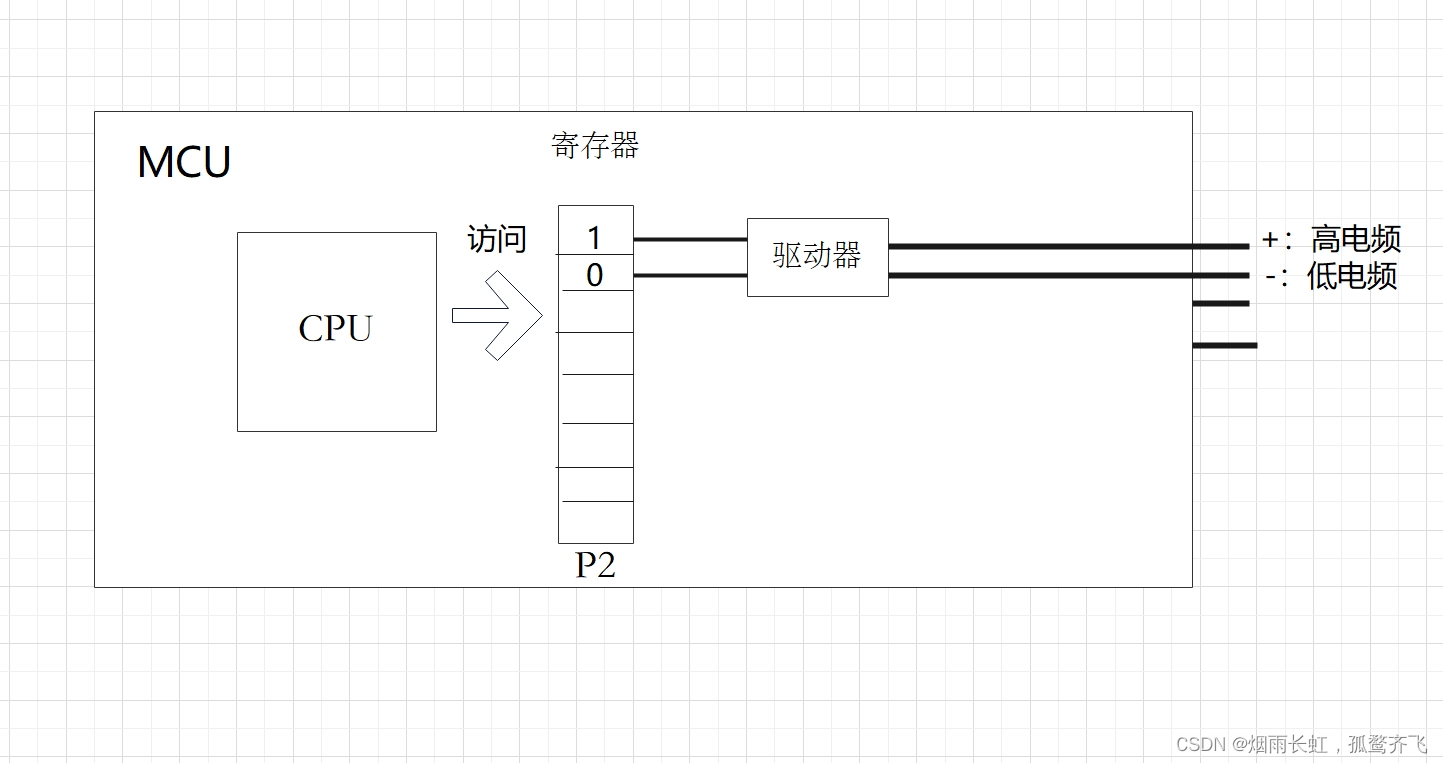
我们可以看到LED连上了单片机的管脚。而单片机需要通过CPU控制寄存器的值,进而通过驱动器加大控制力度,由控制电路输出高低电平
CPU访问寄存器为 1 输出高电频,为 0 输出低电频
点亮LED灯的程序就是让 LED = 0 (低电平),熄灭LED灯的程序就是 LED = 1(高电平)
所以我们只要在对应的寄存器上写 0 或 1 ,即可控制LED的亮灭
点亮一盏LED灯的程序设计
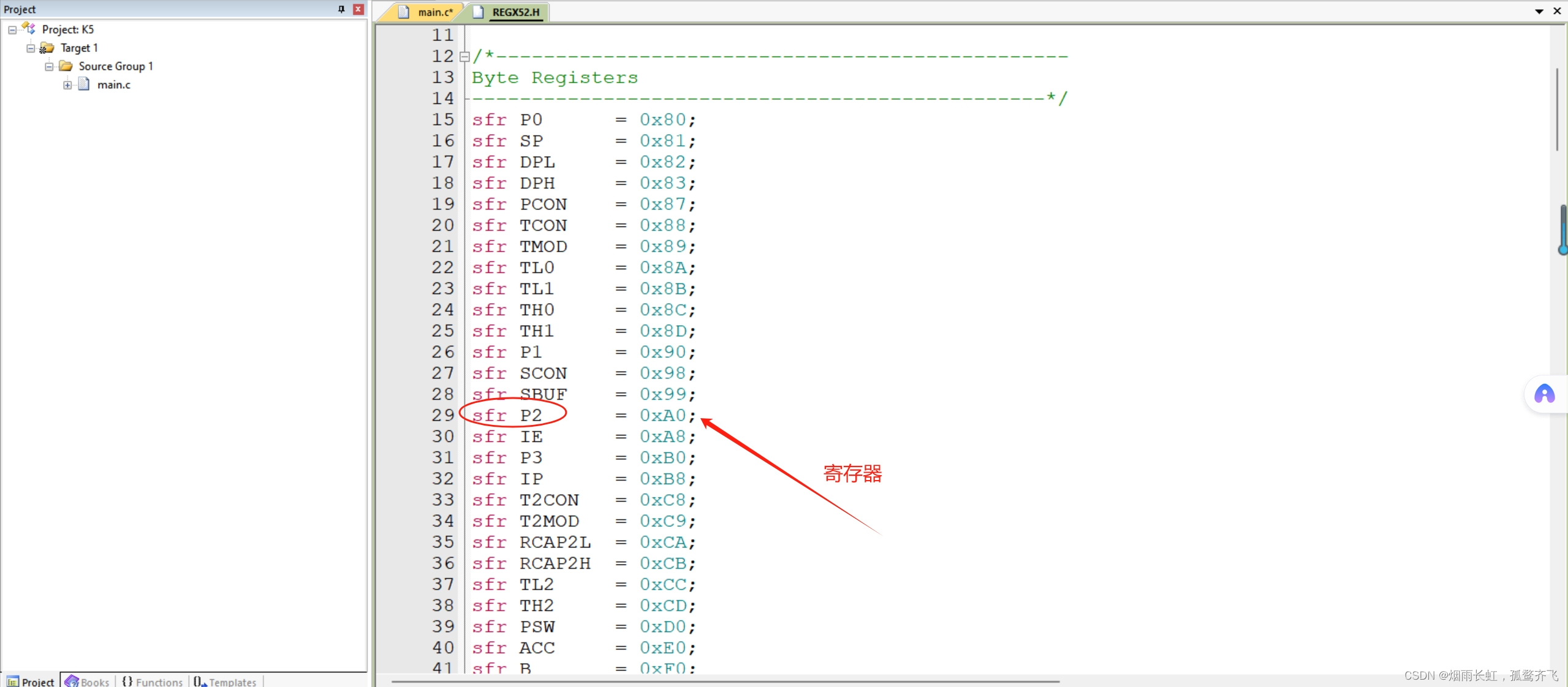
根据硬件原理图和寄存器定义,来对操作寄存器地址,实现灯的点亮
因为单片机只能识别十六进制,所以 1111 1110 要写成0xFE
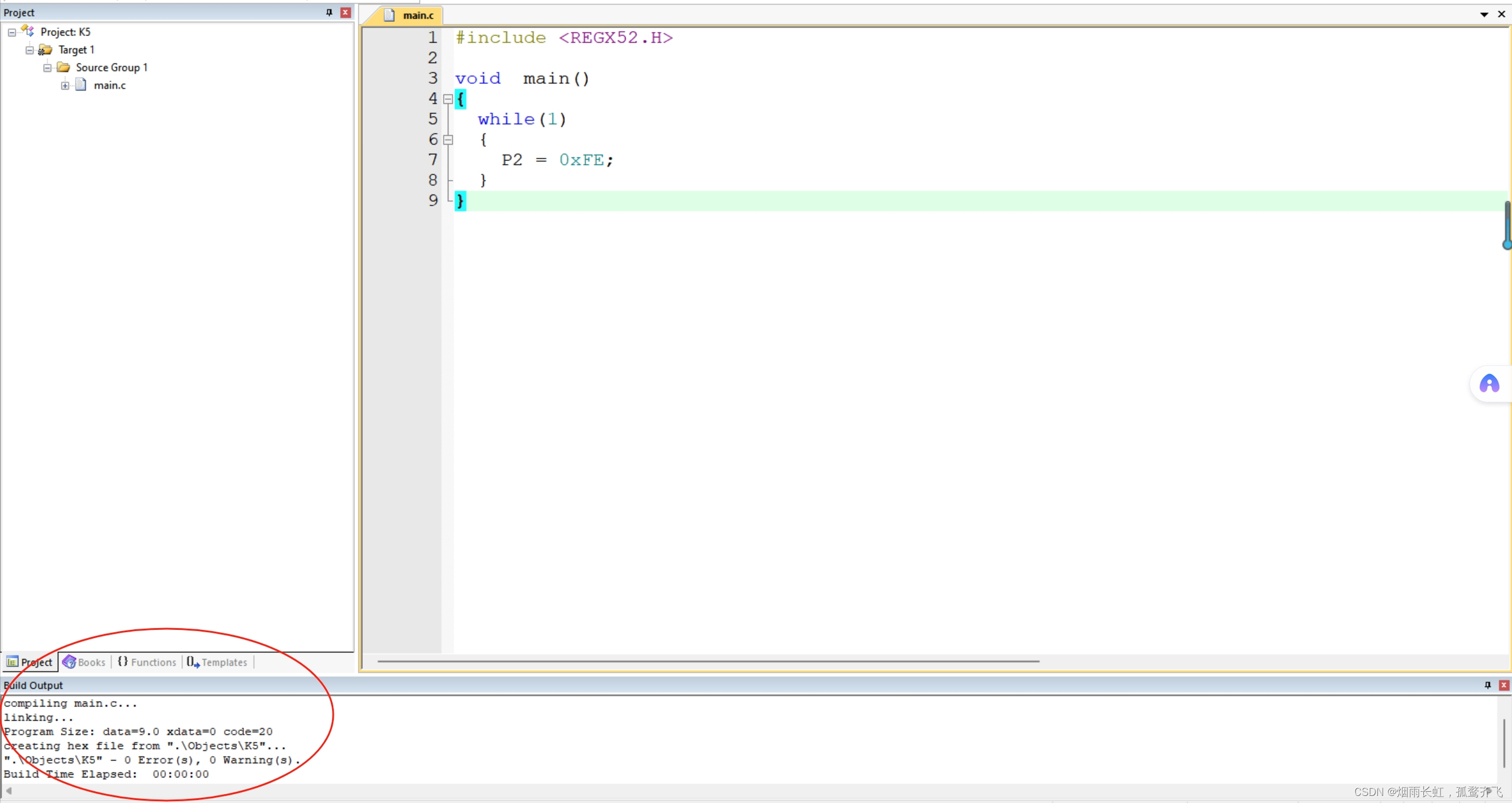
#include <REGX52.H>void main() {while(1){P2 = 0xFE;} }
我们发现这里编译器并没有报任何的错误
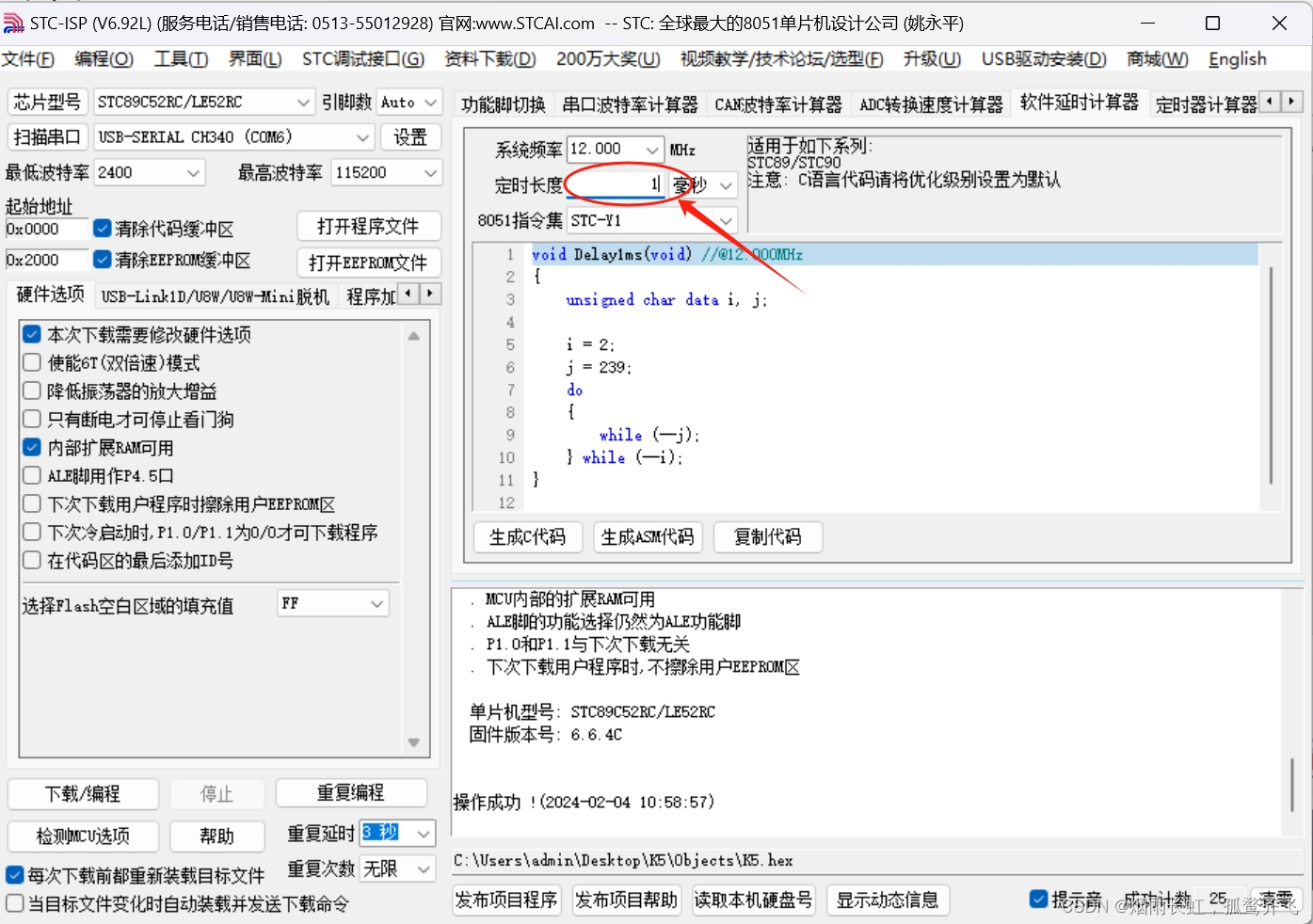
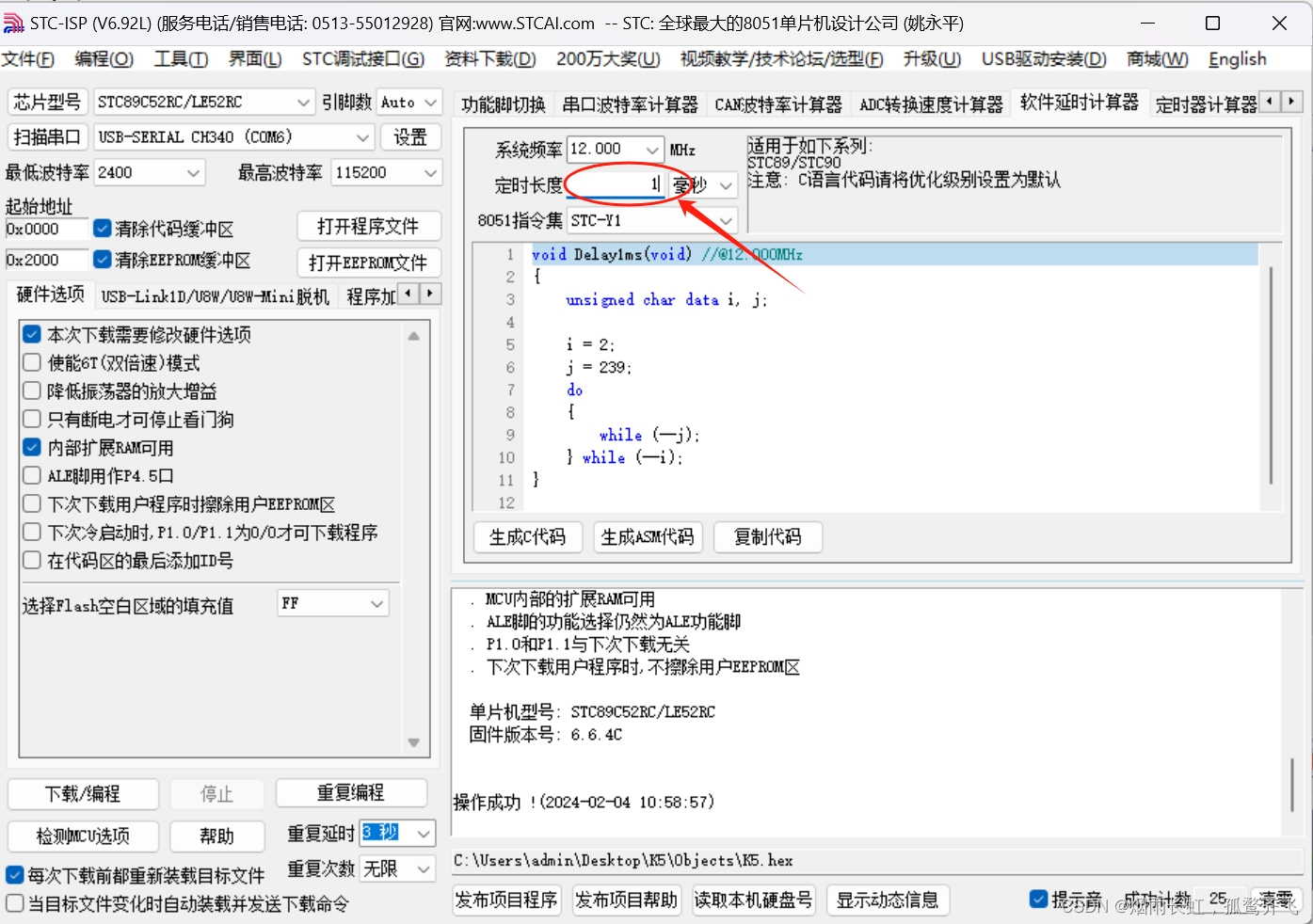
于是我们选择生成文件,将代码下载到板子上
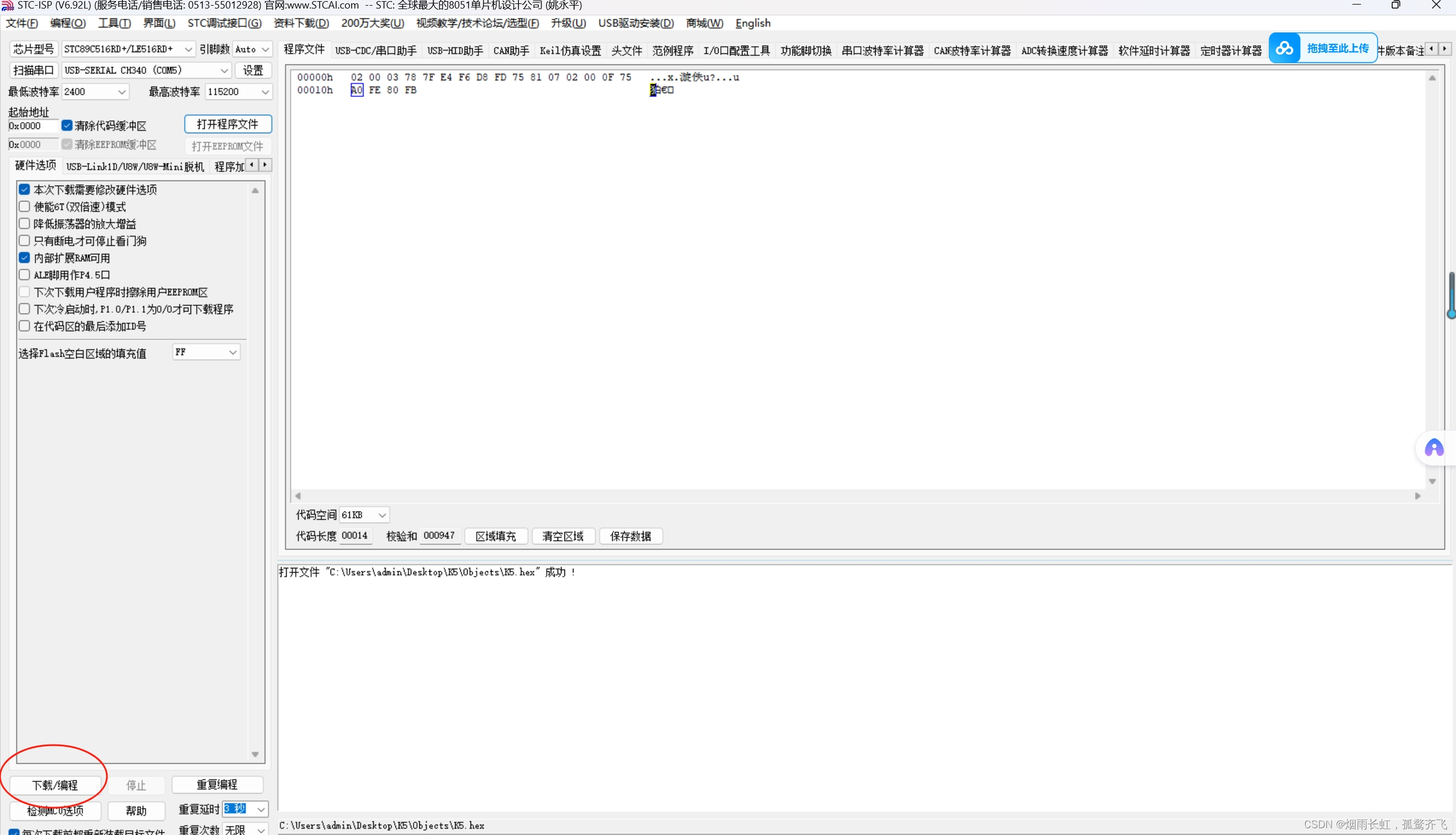
我们找到对应板子的型号,然后打开程序文件,点击下载
这样我们就点亮了一盏LED灯啦
LED灯闪烁
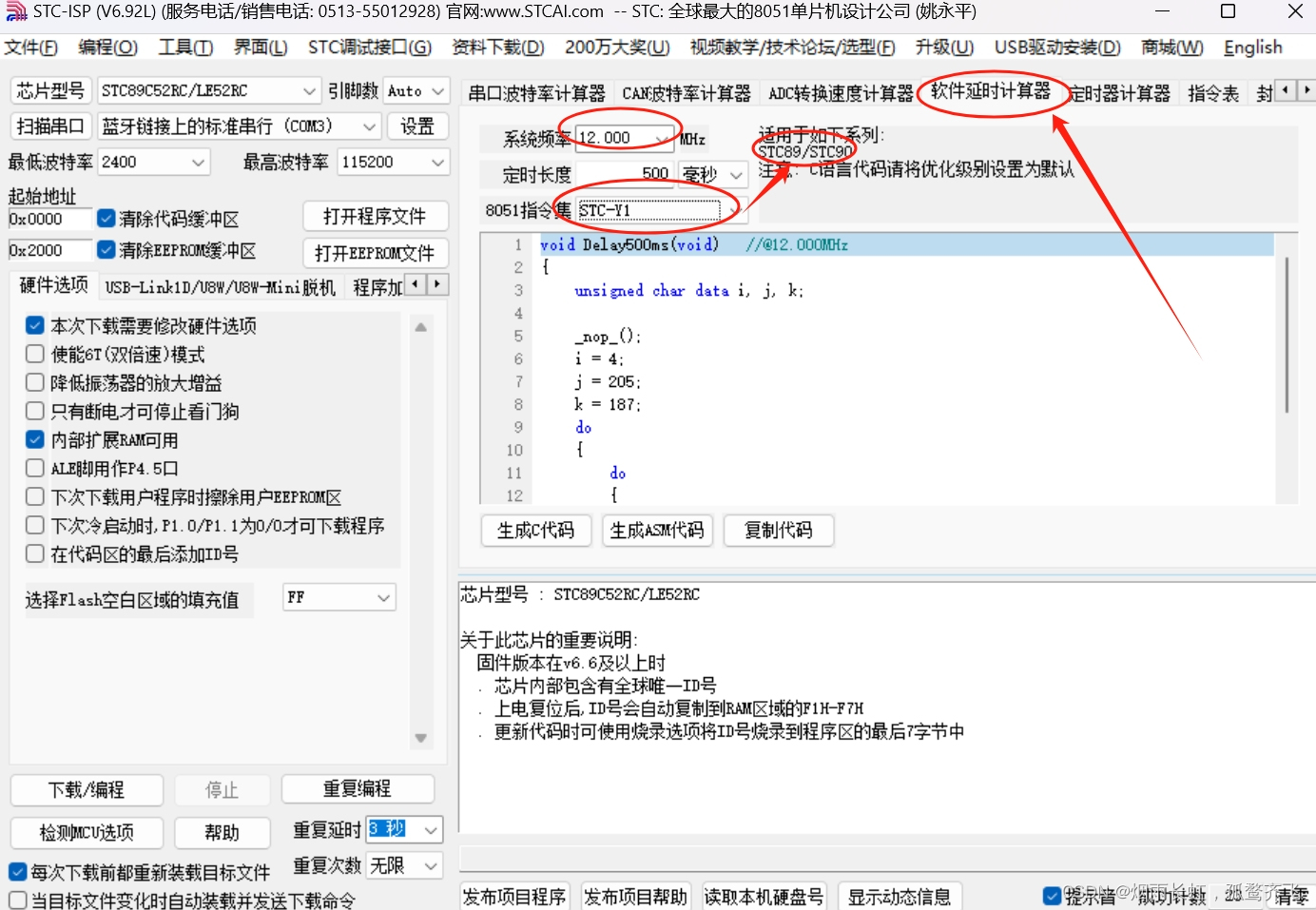
<1>通过STC-ISP拷贝延时代码
<2>加入延时,方便观察灯的闪烁
<3>加上while循环,循环的表达式的值为真,LED就会反复不停的亮和灭
#include <REGX52.H> #include <INTRINS.H>void Delay500ms(void) //@12.000MHz {unsigned char data i, j, k;_nop_();i = 4;j = 205;k = 187;do{do{while (--k);} while (--j);} while (--i); }void main() {while(1){P2 = 0xFE;Delay500ms();P2 = 0xFF;Delay500ms();} }单片机闪烁
LED流水灯
我们学习了点亮LED小灯闪烁,现在我们就可以进一步的让LED灯依次亮起来
这就是我们日常中的流水灯
从之前的代码操作可知,我们可以通过对P2的控制来实现8个LED灯的亮灭
我们只要对P2依次赋值就可以啦:
0xFE、0xFD、0xFB、0xF7、0xEF、0xDF、0xBF、0x7F
#include <REGX52.H> #include <INTRINS.H>void Delay500ms(void) //@12.000MHz {unsigned char data i, j, k;_nop_();i = 4;j = 205;k = 187;do{do{while (--k);} while (--j);} while (--i); }void main() {while(1){P2=0xFE; //1111 1110Delay500ms();P2=0xFD; //1111 1101Delay500ms();P2=0xFB; //1111 1011Delay500ms();P2=0xF7; //1111 0111Delay500ms();P2=0xEF; //1110 1111Delay500ms();P2=0xDF; //1101 1111Delay500ms();P2=0xBF; //1011 1111Delay500ms();P2=0x7F; //0111 1111Delay500ms();} }每次延迟500毫秒太单调了,我们可以让流水灯想延迟多少行秒就可以延迟多少行秒
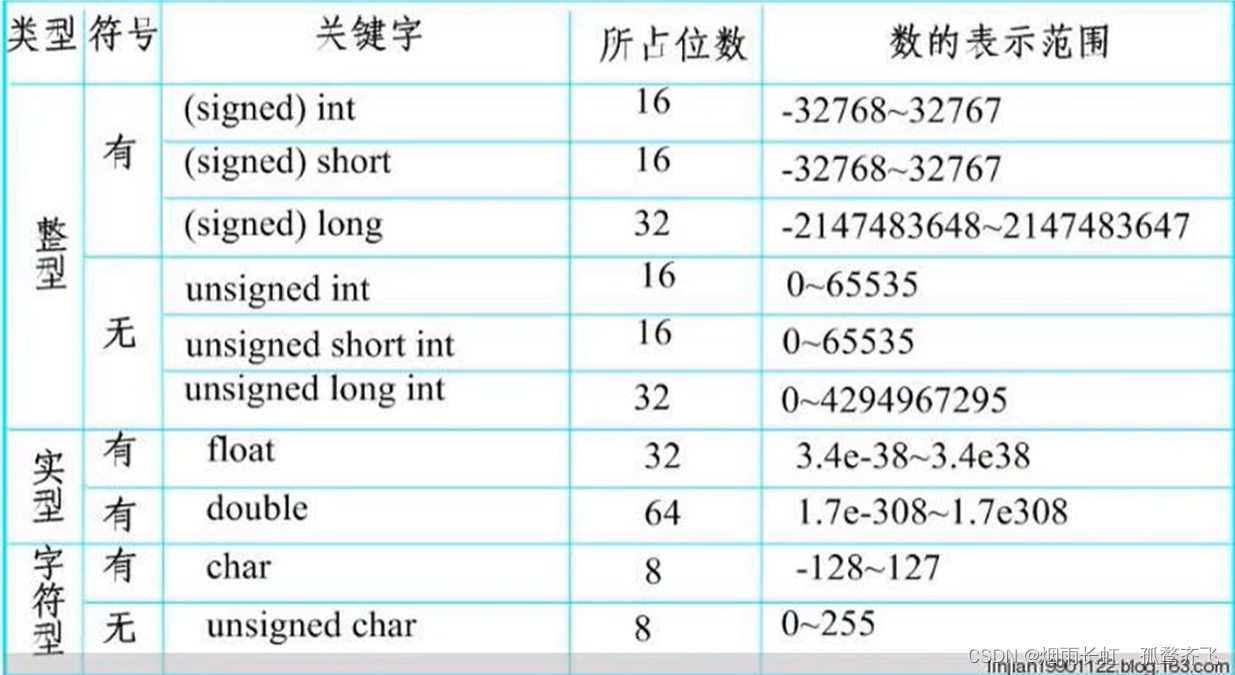
51单片机的数据类型
我们先将 1毫秒 的代码拷贝到我们的编译器上
然后将代码改成 传参类型
void Delay1ms(unsigned int xms) //@12.000MHz {unsigned char data i, j;while(xms){i = 2;j = 239;do{while (--j);} while (--i);xms--;} }这样我们传多少毫秒就延迟多少毫秒
void main() {while(1){P2=0xFE; //1111 1110Delay1ms(100);P2=0xFD; //1111 1101Delay1ms(200);P2=0xFB; //1111 1011Delay1ms(300);P2=0xF7; //1111 0111Delay1ms(400);P2=0xEF; //1110 1111Delay1ms(400);P2=0xDF; //1101 1111Delay1ms(300);P2=0xBF; //1011 1111Delay1ms(200);P2=0x7F; //0111 1111Delay1ms(100);} }
独立按键控制LED灯亮灭
独立按键的组成原理
独立按键直接用 I/O 口线构成的单个按键电路,其特点是每个按键单独占用一根 I/O 口线,每个按键的工作不会影响其他 I/O 口线的状态
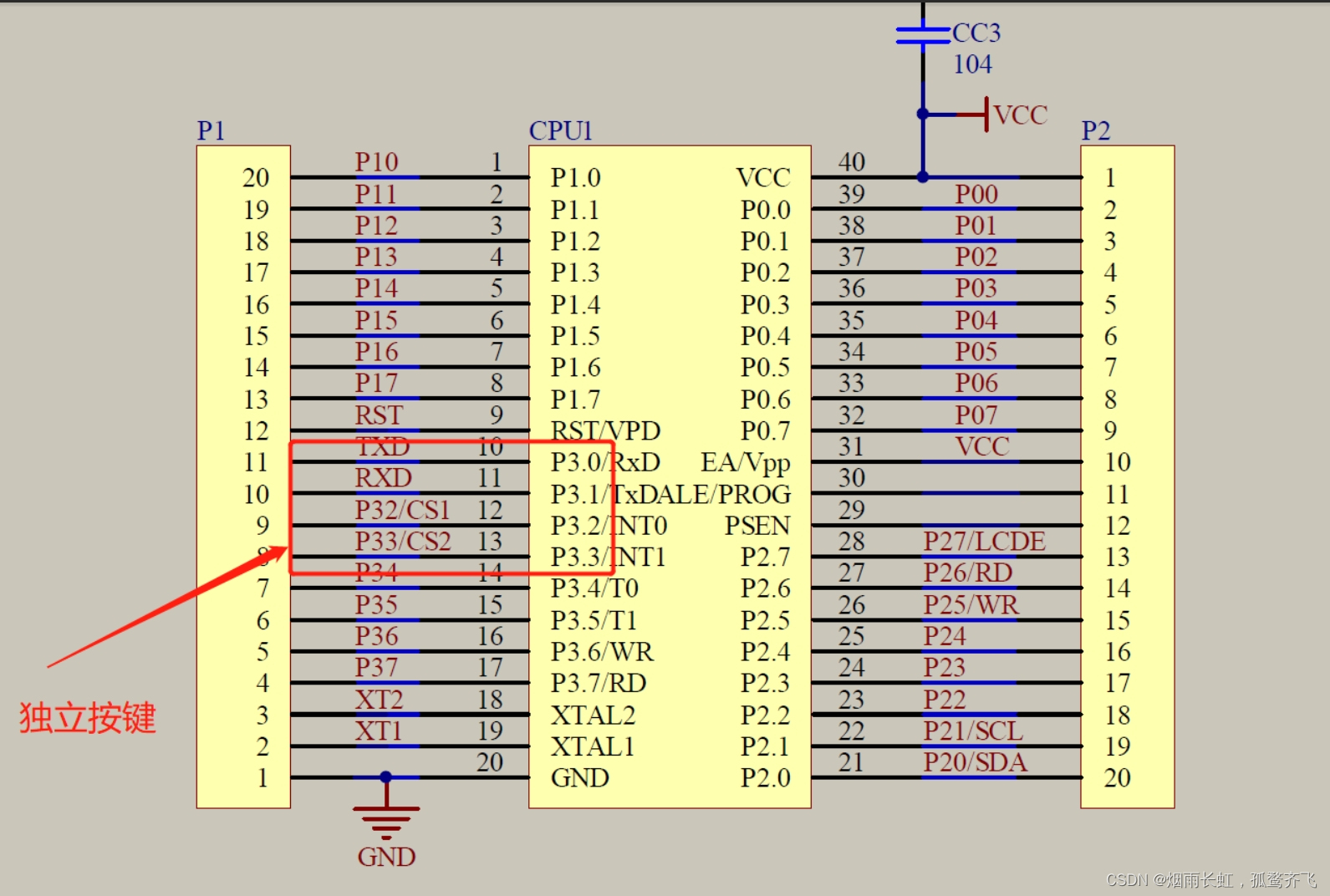
独立按键的硬件模型
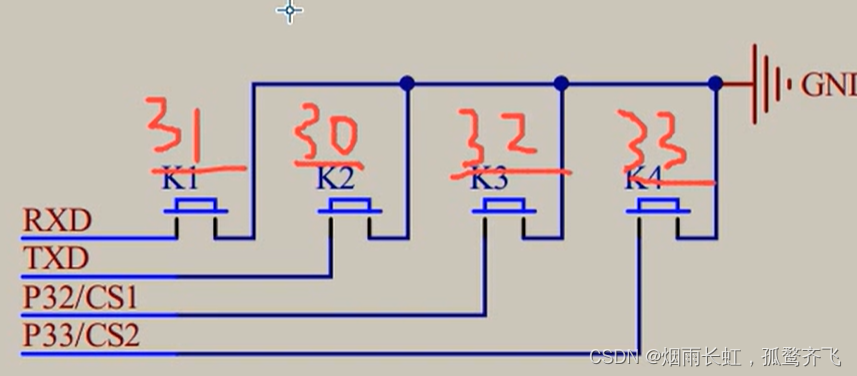
<1>独立按键电路构成是由各个按键的一个管脚连接在一起接地,按键其他引脚分别接到单片机 IO 口
<2>单片机的 IO 口既可作为输出也可作为输入使用,当检测按键时用的是它的输入功能,独立按键的一端接地, 另一端与单片机的 I/O 口相连
<3>开始时先给该 IO 口赋一高电频,然后让单片机不断地检测该 I/O 口是否变为低电频,当按键闭合时,即相当于该 I/O 口通过按键与地相连,变成低电频,程序一旦检测到I/O 口变为低电频则说明按键被按下,然后执行相应的指令
当按下k1时,LED小灯D1亮起,松开按键时D1灭掉
#include <REGX52.H>void main() {P2_0 = 1; while(1){if(P3_1 == 0) //检测按键判断是否点亮LED灯{P2_0 = 0; }else{P2_0 = 1; }} }
独立按键控制LED灯状态
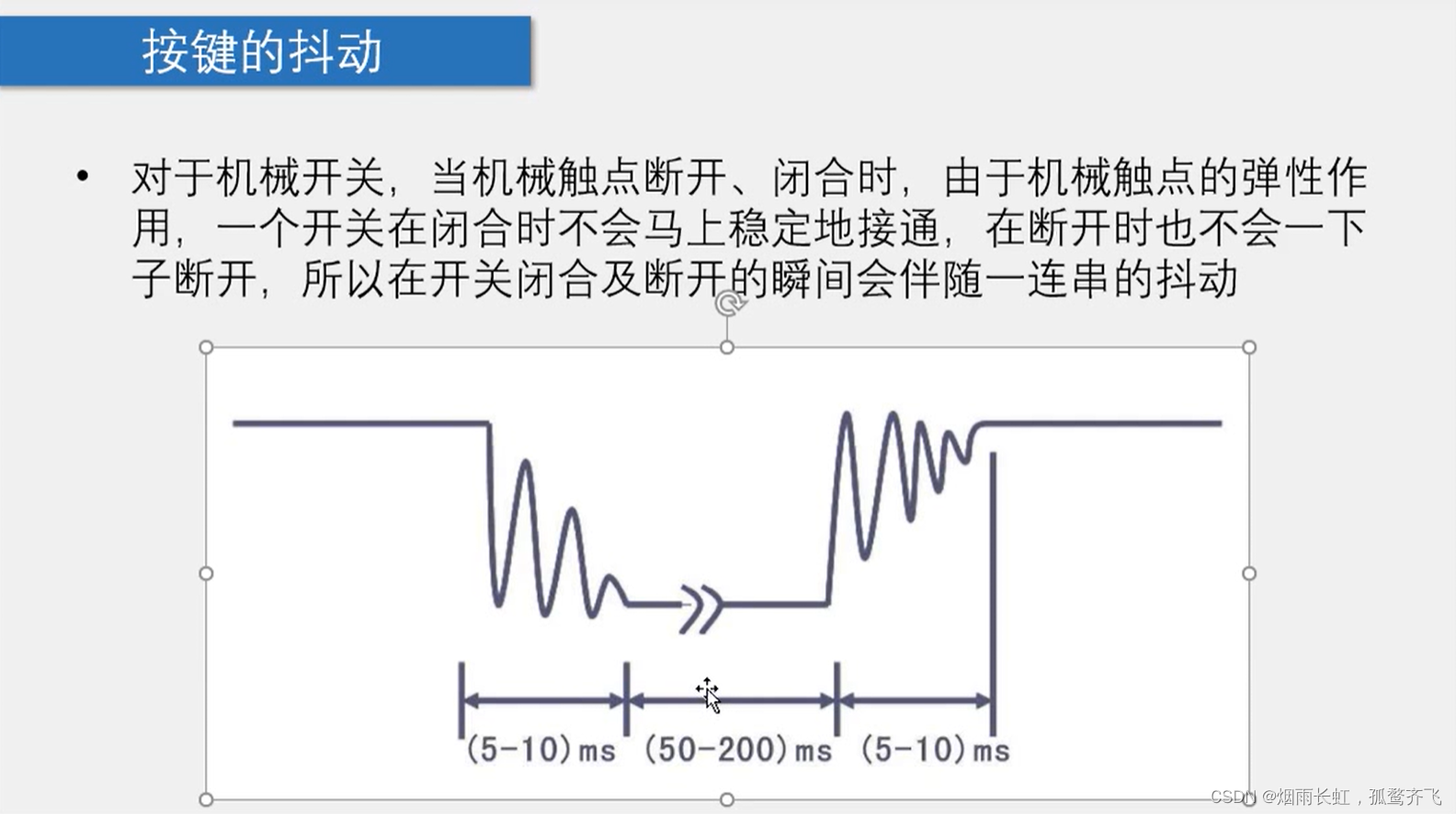
按键的抖动
通常按键所用的开关都是机械弹性开关,当机械触点断开、闭合时,由于机械触点的弹性作用,一个按键开关在闭合时不会马上就稳定接通,在断开时也不会一下子彻底断开,而是在闭合和断开的瞬间伴随了一连串的 抖动
按键的效抖
<1>硬件消抖:按键上并联一个电容,利用电容的充放电特性对抖动过程中产生的电压毛刺进行平滑处理,从而实现消抖
<2>软件消抖:通过对按键状态进行两次检测,并引入适当的延时,从而忽略前沿抖动的影响
#include <REGX52.H>void Delay(unsigned int xms) //单位毫秒的延时函数 {unsigned char i, j;while(xms){i = 2;j = 239;do{while (--j);} while (--i);xms--;} }void main() {while(1){if(P3_1 == 0) //当按键按下时K1会与地相连 引脚处会被置低电频,D1点亮{Delay(20); //延迟20毫秒while(P3_1 == 0); //当再次按下K1键,引脚处会被置高电频Delay(20);P2_0 =~P2_0; //D1按位取反,回到高电频,D1关闭}} }首先检测按键是否处于按下状态,然后进行一段较短时间的延时,再次检测按键状态。如果确认按键仍然被按下,则执行相应的操作(在示例中为 取反 操作),并延时一段时间来避免连续按下造成的快速闪烁。最后,使用一个 while循环 来等待按键被释放
独立按键控制LED灯移位
通过控制独立按键K1、K2来实现左右移位
位移的原理
#include <REGX52.H>void Delay(unsigned int xms) //1毫秒的延迟函数 {unsigned char i, j;while(xms--){i = 2;j = 239;do{while (--j);} while (--i);} }unsigned char LEDNum; //全局变量初始化为0 void main() {P2 = ~0x01; //给P2按位取反就是点亮D1while(1){if(P3_1 == 0) //检测K1键有没有按下{Delay(20); while(P3_1 == 0); //消抖Delay(20);LEDNum++; //LEDNum自增//随着K1按键按下,LEDNum二进制变大,LED灯也会往右依次亮起if(LEDNum>=8) //处理边界问题LEDNum = 0;P2 = ~(0x01<<LEDNum); //LED的第LEDNum位点亮}if(P3_0 == 0){Delay(20);while(P3_0 == 0);Delay(20);if(LEDNum == 0)LEDNum = 7;elseLEDNum--;P2 = ~(0x01<<LEDNum);}} }