网站怎么推广最免费建站 永久
文章目录
- 1. 介绍
- 2. 实例使用
- 2.1 登录界面
- 2.2 对比两次密码是否相同
- 2.3 通过按钮显示当前输入的密码(并对2.2进行优化)
- 2.4 结语
- 3. 正则表达式
- 3.1 QRegExp
- 3.2 验证输入内容
- 4. 资源代码
1. 介绍
关于 QLineEdit 的详细介绍,可以去查阅官方文档,这里简单进行总结:
- QLineEdit是Qt框架中的一个类,用于创建单行文本输入框。
- 它允许用户输入和编辑单行文本,可以用于接受用户输入的各种数据,比如用户名、密码、搜索关键字等。
- QLineEdit提供了一些属性和方法来管理文本输入、校验输入内容以及响应用户操作。
下面是QLineEdit的 核心属性 :
| 属性 | 描述 |
|---|---|
| text | 当前文本内容 |
| placeholderText | 占位符文本,当输入框为空时显示 |
| maxLength | 最大长度限制 |
| inputMask | 输入掩码,限制输入格式 |
| readOnly | 只读状态 |
| alignment | 对齐方式 |
| validator | 输入内容验证器 |
| frame | 是否显示边框 |
| echoMode | 输入内容显示模式(如密码模式) |
| cursorPosition | 光标位置 |
| dragEnabled | 是否启用拖放 |
| clearButtonEnabled | 是否显示清除按钮 |
| modified | 文本内容是否被修改 |
| cursorMoveStyle | 光标移动样式 |
根据上面的核心属性:用户可以设置输入框的默认文本、最大长度、输入掩码(用于限制输入格式)、校验器(用于验证输入的合法性)等。
2. 实例使用
2.1 登录界面
- 我们首先在Designer下进行如下 布局 :

- 随后在
widget.cpp中的 构造函数 中对每个输入框进行属性设置:
Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget)
{ui->setupUi(this);// 给每个输入框 设置相关属性ui->lineEdit_account->setPlaceholderText("输入账号/用户名"); // 设置默认提示信息ui->lineEdit_account->setClearButtonEnabled(true); // 设置一键删除ui->lineEdit_password->setPlaceholderText("输入密码");ui->lineEdit_password->setClearButtonEnabled(true);ui->lineEdit_password->setEchoMode(QLineEdit::Password); // 将显示模式设置为密码ui->lineEdit_email->setPlaceholderText("输入邮箱");ui->lineEdit_email->setClearButtonEnabled(true);ui->lineEdit_email->setInputMask("XXXXXXXXXXXXXXX.com"); // 设置格式条件
}
- 随后对 按钮点击的槽函数 进行编写:
- 点击提交按钮后,会弹出窗口显示用户的信息:
void Widget::on_pushButton_clicked()
{QString account = ui->lineEdit_account->text();QString password = ui->lineEdit_password->text();QString email = ui->lineEdit_email->text();QString gender = ui->radioButton_male->isChecked() ? "男" : "女";// 创建一个弹出窗口来显示填入的信息QMessageBox msgBox;msgBox.setText("账号/用户名: " + account + "\n"+ "密码: " + password + "\n"+ "邮箱: " + email + "\n"+ "性别: " + gender);msgBox.exec();
}
结果演示:
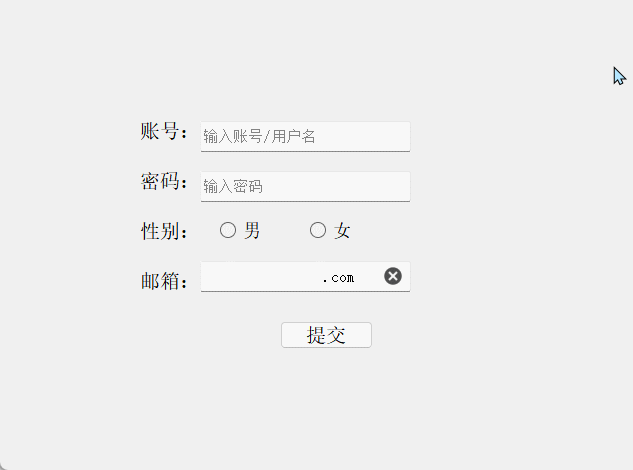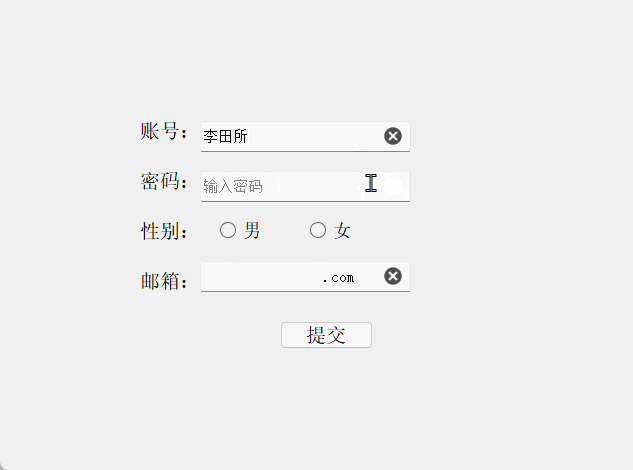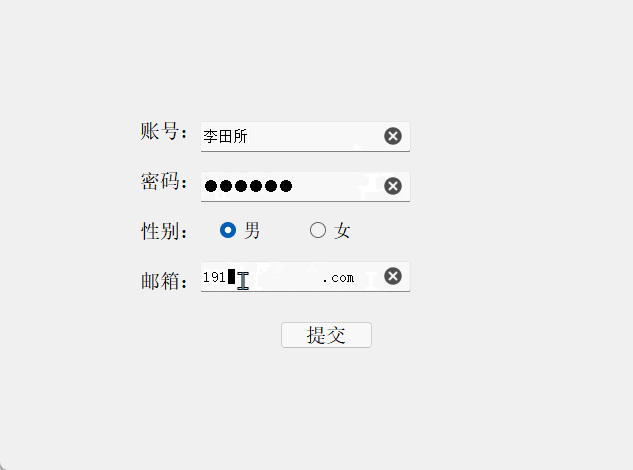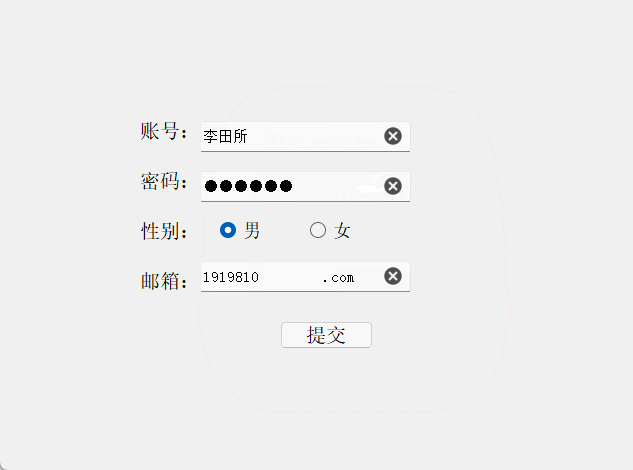
2.2 对比两次密码是否相同
我们一般在网站创建用户,修改密码时,都会有两个密码框,让我们再次确认密码,这里就进行实现:
- 我们首先在Designer界面进行如下布局:
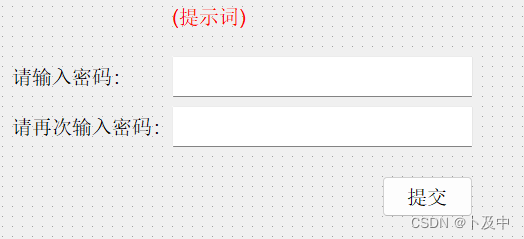
- 在
widget.h中进行 槽函数等定义 :
public:Widget(QWidget *parent = nullptr);~Widget();// 用于比较两文本框内容void comparePwd();private slots:// 按钮槽函数void on_pushButton_clicked();
- 在
widget.cpp中在构造函数中设置两文本框属性 + 连接文本框与比较函数:
Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget)
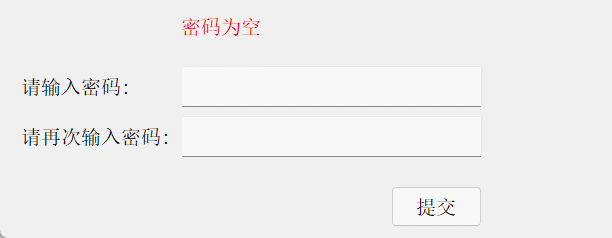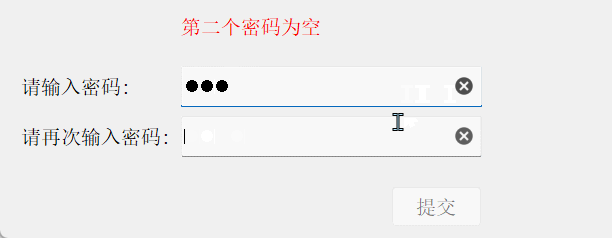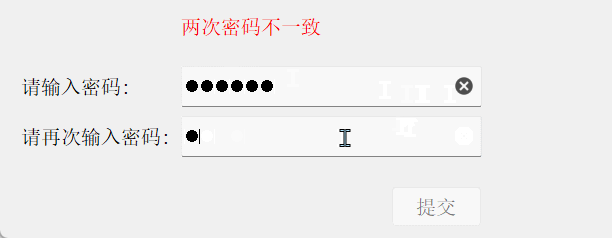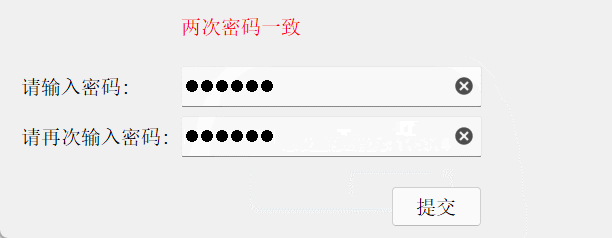
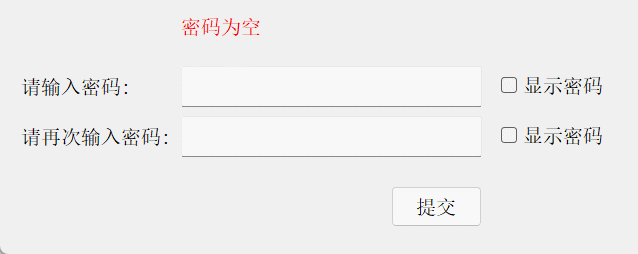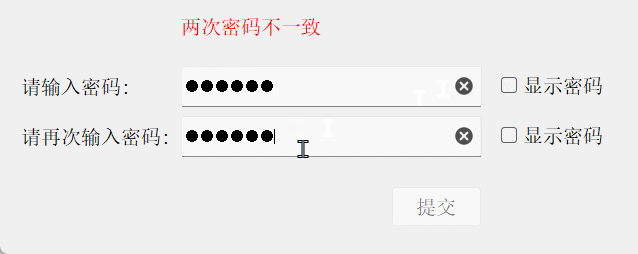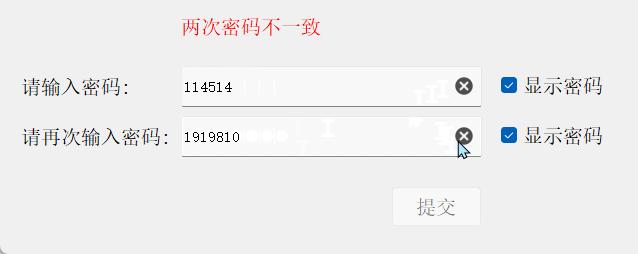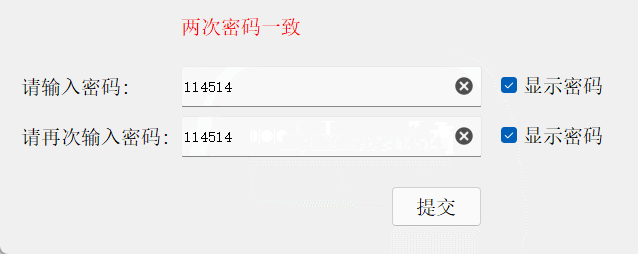
{ui->setupUi(this);// 给文本框设置相关模式ui->lineEdit_1->setEchoMode(QLineEdit::Password);ui->lineEdit_1->setClearButtonEnabled(true);ui->lineEdit_2->setEchoMode(QLineEdit::Password);ui->lineEdit_2->setClearButtonEnabled(true);ui->label->setText("密码为空");// 连接文本框的状态 与比较函数,用于实时传出两密码信息connect(ui->lineEdit_1, &QLineEdit::textEdited, this, &Widget::comparePwd);connect(ui->lineEdit_2, &QLineEdit::textEdited, this, &Widget::comparePwd);
}- 随后在
widget.cpp中对上面的函数进行实现:
void Widget::comparePwd()
{// 比较两密码状态const QString& s1 = ui->lineEdit_1->text();const QString& s2 = ui->lineEdit_2->text();if(s1.isEmpty() && s2.isEmpty()){ui->label_prompt->setText("密码为空");ui->pushButton->setEnabled(false);}else if(s1 == s2){ui->label_prompt->setText("两次密码一致");ui->pushButton->setEnabled(true);}else{if (s1.isEmpty()) {ui->label_prompt->setText("第一个密码为空");} else if (s2.isEmpty()) {ui->label_prompt->setText("第二个密码为空");} else {ui->label_prompt->setText("两次密码不一致");}ui->pushButton->setEnabled(false);}
}void Widget::on_pushButton_clicked()
{// 提取密码,弹出对话框显示密码QString Password = ui->lineEdit_1->text();QMessageBox msgBox;msgBox.setText("您设置的密码为: " + Password);msgBox.exec();
}
对于上面的代码,
(void) arg1的作用:为了避免编译器产生未使用变量的警告。
结果演示:
2.3 通过按钮显示当前输入的密码(并对2.2进行优化)
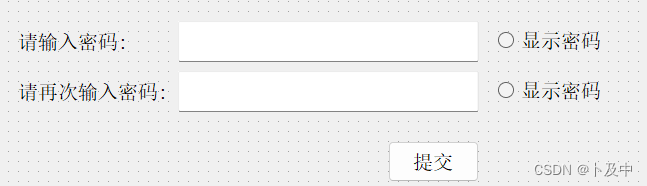
我们在网站中输入密码时,一般允许点击按钮来显示当前密码,这里用一个checkBox(复选框)来进行这样的功能:(在例2.2的前提下继续编写)
- 首先添加两个按钮,分别用于 将两文本框的密码可视化 :
- 分别编写两个按钮的槽函数,我们可以将可视化密码的代码封装为函数,首先在
widget.h中添加如下函数:
public:// 可视化密码void togglePasswordVisibility();private slots:// 按钮槽函数void on_checkBox_1_toggled(bool checked);void on_checkBox_2_toggled(bool checked);
- 后在
widget.cc中对上面函数进行实现:
// 两checkBox 用于显示两文本框中的密码
void Widget::togglePasswordVisibility()
{bool showPassword1 = ui->checkBox_1->isChecked();bool showPassword2 = ui->checkBox_2->isChecked();ui->lineEdit_1->setEchoMode(showPassword1 ? QLineEdit::Normal : QLineEdit::Password);ui->lineEdit_2->setEchoMode(showPassword2 ? QLineEdit::Normal : QLineEdit::Password);comparePwd(); // 每次切换密码可视化状态时重新比较密码
}void Widget::on_checkBox_1_toggled(bool checked)
{togglePasswordVisibility();
}void Widget::on_checkBox_2_toggled(bool checked)
{togglePasswordVisibility();
}
结果演示:
2.4 结语
我们可以将登录界面与 后两个例子的内容结合, 完善出一个 “登录界面” 的功能。
3. 正则表达式
正则表达式(Regular Expression):是一种文本模式,用于匹配、搜索和替换文本中的字符串。
下面列举了一些常见的正则表达式内容及其含义:
| 正则表达式 | 含义 |
|---|---|
| . | 匹配任意单个字符 |
| ^ | 匹配字符串的开头 |
| $ | 匹配字符串的结尾 |
| * | 匹配前面的字符零次或多次 |
| + | 匹配前面的字符一次或多次 |
| ? | 匹配前面的字符零次或一次 |
| [] | 匹配一组中括号中的任意一个字符 |
| [^] | 匹配除了中括号中指定的字符之外的任意一个字符 |
| () | 捕获匹配的字符串,以供后续使用 |
3.1 QRegExp
QRegExp是Qt中用于处理正则表达式的类,它提供了一系列函数用于匹配、搜索和替换文本中的字符串。
- 下面列举了
QRegExp类的一些常用接口函数及其作用:
| 接口函数 | 作用 |
|---|---|
QRegExp(const QString &pattern) | 构造函数,使用给定的正则表达式模式初始化 QRegExp 对象 |
exactMatch(const QString &str) | 检查给定的字符串是否与正则表达式完全匹配 |
indexIn(const QString &str, int offset = 0) | 在给定的字符串中搜索正则表达式的第一个匹配项,并返回其位置 |
pos() | 返回最后一次匹配的子串在字符串中的起始位置 |
matchedLength() | 返回最后一次匹配的子串的长度 |
capturedTexts() | 返回最近一次匹配操作中捕获的所有子串 |
replace(QString *str, const QString &after) | 使用给定的字符串替换匹配正则表达式的第一个子串 |
globalReplace(QString *str, const QString &after) | 使用给定的字符串替换匹配正则表达式的所有子串 |
下面进行实例:
3.2 验证输入内容
这里主要用 QRegExp验证 输入框中输入的内容是否合法
比如,验证输入的手机号是否合法:
- 首先简单在Designer界面如下布局:

- 在widget.cc的构造函数中写下面的代码:
QRegExp regExp("^1\\d{10}$");
解释: 用于匹配中国大陆手机号码的正则表达式。
^表示字符串的开始1表示手机号码必须以数字1开头\\d表示任意数字{10}表示前面的\d必须出现10次,即手机号码应该是11位数$表示字符串的结束
该正则表达式可以匹配所有以数字1开头,且后面跟着10个数字的字符串,符合国内手机号码的格式。
- 继续补充代码:
Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget)
{ui->setupUi(this);QRegularExpression regExp("^1\\d{10}$");QValidator *validator = new QRegularExpressionValidator(regExp, this);ui->lineEdit_number->setValidator(validator);
}
解释:
QValidator是 Qt 提供的用于验证用户输入的基类,QRegExpValidator是QValidator的子类,用于基于正则表达式对用户输入进行验证。
-
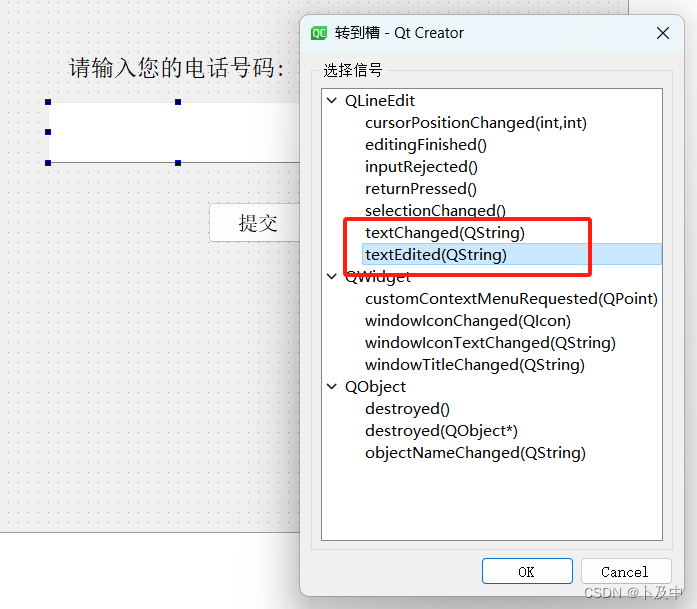
随后直接对 文本框 进行槽函数的编写:
textEdited用于相应文本框中的变化,texdtChanged与textEdited两者功能类似:
-
在槽函数中编写 验证的代码:
void Widget::on_lineEdit_number_textEdited(const QString &arg1)
{QString content = text; // 获取文本框内容int pos = 0;if(ui->lineEdit_number->validator()->validate(content, pos) == QValidator::Acceptable)ui->pushButton_verify->setEnabled(true);elseui->pushButton_verify->setEnabled(false);
}
对于if语句中的内容:
这行代码是在检查用户输入的内容是否符合 QLineEdit 中设置的验证器(validator)的要求。具体来说,这行代码做了以下操作:
ui->lineEdit_number->validator():获取QLineEdit中设置的验证器对象。validate(content, pos):通过验证器对给定的content内容进行验证,pos是一个输出参数,表示验证通过后的位置信息。QValidator::Acceptable:表示验证器接受(Acceptable)给定的内容。
因此,整个条件判断的含义是:如果用户输入的 content 内容经过 lineEdit_number 的验证器验证后被认为是可接受的(Acceptable),则条件成立。
结果演示:
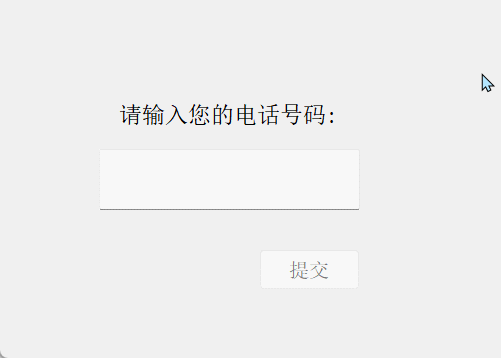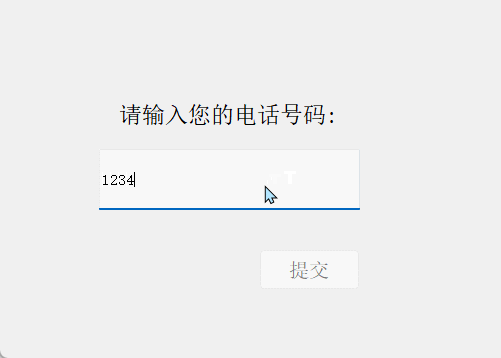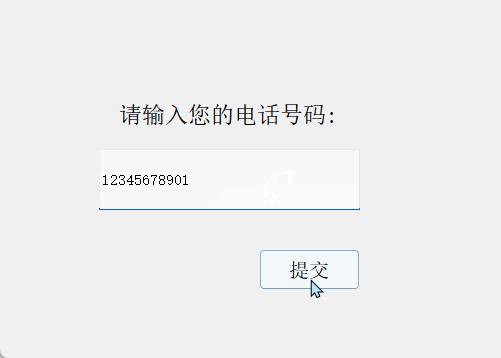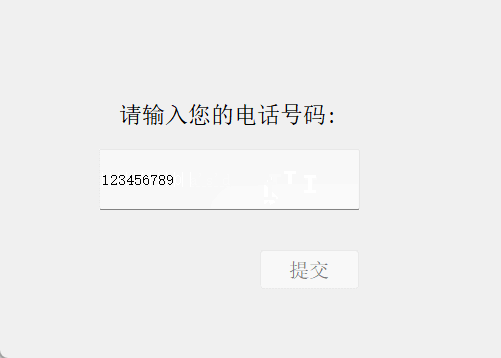
4. 资源代码
上文中涉及的所有代码等资源👇:
2.1 QLineEdit的使用 - 简单的登录界面
2.2 / 2.3 QLineEdit的使用 - 密码验证
3.1 QLineEdit的使用 - 正则表达式与QRegExp
