免费做网站网站做外贸什么网站
目录
netstat
pidof
UDP协议
TCP协议
TCP协议段格式
TCP协议的相关机制
确认应答(ACK)机制
超时重传机制
连接管理机制
服务端状态转换
客户端状态转化
流量控制
流量控制常见问题:
滑动窗口
拥塞控制
延迟应答
面向字节流
粘包问题
TCP异常情况
传输层的作用就是负责数据能够从发送端接收数据
端口号
端口号(Port)标识了一个主机上进行通信的不同应用程序;
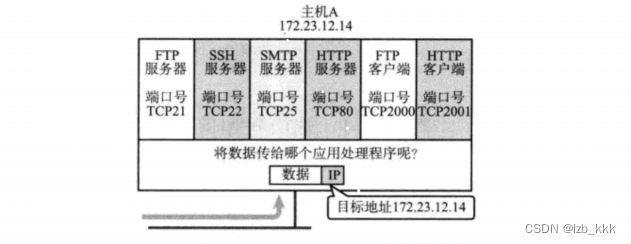
在TCP/IP协议中,用“源IP”,“源端口号”,“目的IP”,“目的端口号”,“协议号”这样一个五元组来标识一个通信(可以通过netstat -n查看)
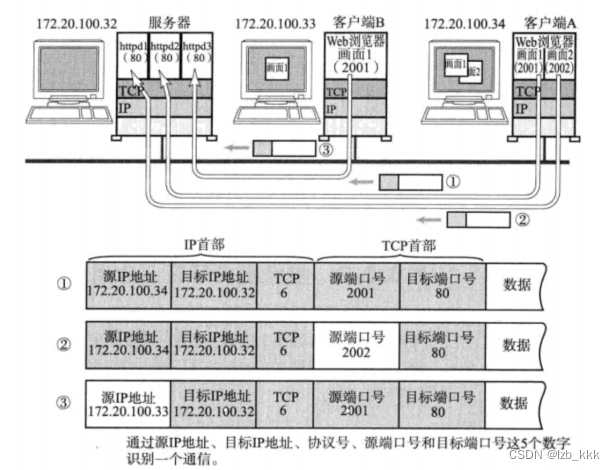
端口号范围的划分
0 - 1023:知名端口号,HTTP,FTP,SSH 等这些广为使用的应用层协议,他们的端口号都是固定的。
认识知名端口号
- ssh服务器, 使用22端口
- ftp服务器, 使用21端口
- telnet服务器, 使用23端口
- http服务器, 使用80端口
- https服务器, 使用443
执行下面的命令,可以看到知名端口号
cat /etc/services
两个问题
- 一个进程是否可以bind多个端口号?
- 一个端口号是否可以被多个进程bind?
netstat
netstat是一个用来查看网络状态的重要工具
语法 : netstat [ 选项 ]功能 :查看网络状态常用选项 :
- n 拒绝显示别名,能显示数字的全部转化成数字
- l 仅列出有在 Listen (监听) 的服務状态
- p 显示建立相关链接的程序名
- t (tcp)仅显示tcp相关选项
- u (udp)仅显示udp相关选项
- a (all)显示所有选项,默认不显示LISTEN相关
pidof
在查看服务器的进程 id 时非常方便 .语法 : pidof [ 进程名 ]功能 :通过进程名 , 查看进程 id,常用来查看守护进程
UDP协议
UDP协议端格式

UDP长度-8字节(报头)= 有效载荷的长度
- 16位UDP长度, 表示整个数据报(UDP首部+UDP数据)的最大长度;
- 如果校验和出错, 就会直接丢弃;
TCP协议
TCP全称为 "传输控制协议(Transmission Control Protocol"). 人如其名, 要对数据的传输进行一个详细的控制;
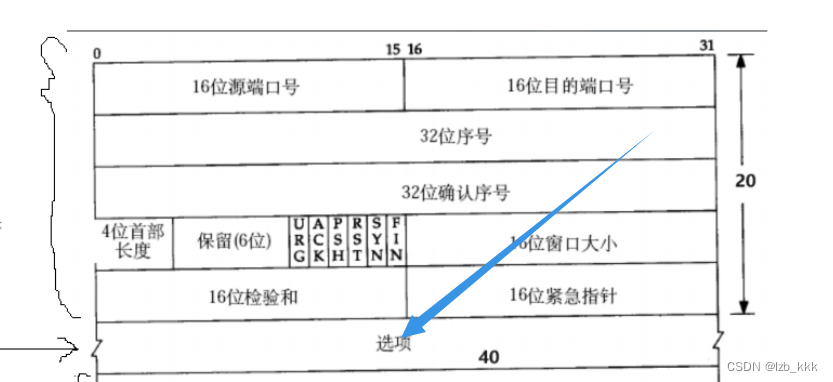
TCP协议段格式

4位的首部长度描述的报头的长度,计算的时候,有基本的大小单位:4字节
例如 x*4=20 ,x取5 也就是0101
如果不进行流量控制,会导致大面积丢包
16位窗口大小就是对方接收缓冲区剩余空间,也就是进行流量控制的依据
tcp协议不同于http协议的是双方都会进行收发数据
TCP最基本、最原始的通信过程

收到应答信号,确认最近发送的信息对方收到了,没有应答的数据,我们无法保证可靠性,所以,最新的一条信息,是没有应答的,所以我们无法保证发出去的信息是100%可靠的。
综上,世界上是不存在100%可靠的网络协议,但是局部性的可靠性是可以保证的。
一段时间后,如果没有收到应答,就认为数据丢失了,进行重传。
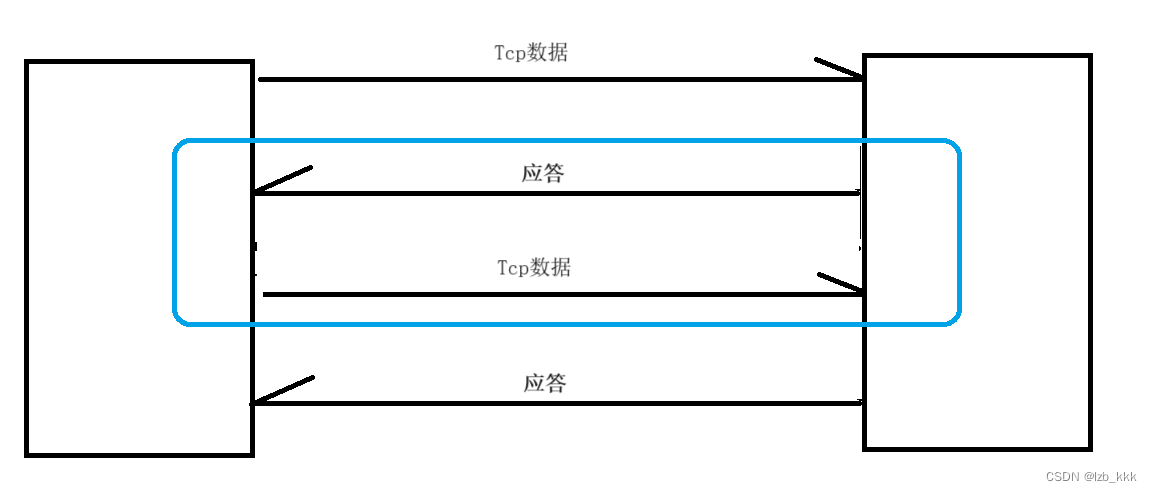
将应答和下一个TCP数据二合一发送给对方,这种策略称为捎带应答
乱序问题
那么接下来有一个问题,如果客户端发送tcp数据给服务器,服务器没有返回应答信号,客户端是否继续发送下一条数据?
如果采用发一条数据,应答一个的方式,效率会很低,因此客户端一般一次给服务器发送一批数据

服务器数据的接收顺序并不一定是客户端发送数据的顺序 ,这种问题称为数据包乱序问题。这种情况如果不解决,直接将数据交到缓冲区,会导致应用层解析数据报文错误。造成乱序本身就是不可靠的一种。
为了解决这种问题,引入序号,给每个报文加上序号,发送到服务端,即使服务端收到的是乱序的,也可以通过序号进行还原。
如下图所示:

综上,也就是说32位序号是为了保证数据的按序到达
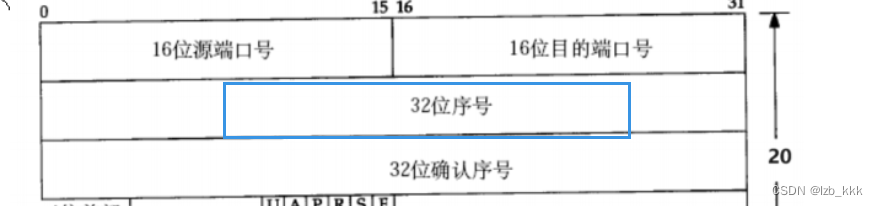
服务端接收到客户端的一批tcp数据后,会返回多个应答数据,那么怎么区分某个应答是对应哪个tcp数据呢?
确认序号:填充的是它收到的报文的序号+1
为什么要这么规定?
确认序号的意义:表示确认序号之前的数据,已经全部收到了,下一次发送,请从确认序号指定的数字开始发送!!

当应答返回3001,而2001、1001未返回相应应答 ,服务端默认3001之前已经全部收到了,这样的规定允许应答能有少量的丢失。
tcp收到的报文一定是由各种“类型”的,不同的类型,决定了服务端做不同的动作!接收方如何得知报头的类型是什么?用6个标记位,标记位存在的意义:区分tcp报文的类型
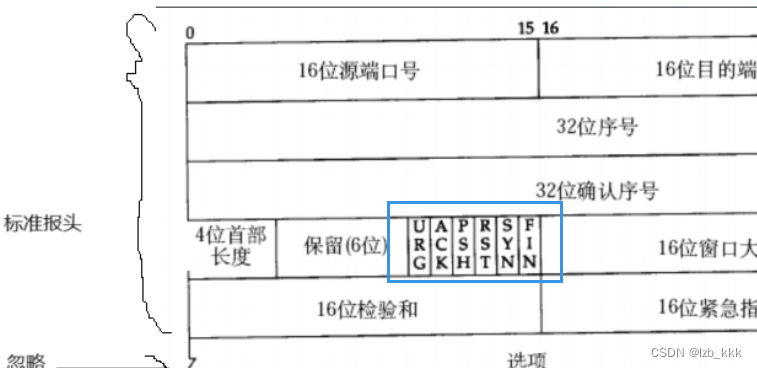
ACK :确认序号是否有效
SYN:请求建立连接,我们把携带SYN标识的称为同步报文段
FIN:通知对方,本端要关闭了
PSH:提示接收端应用程序立刻从TCP缓冲区把数据读走
RST:对方要求重新建立连接,我们把携带RST标识的称为复位报文段
URG:紧急指针是否有效
16位紧急指针:当前报文包含紧急数据的偏移量是多少,紧急数据为一个字节,称为带外数据,缓冲区排队的数据是常规数据
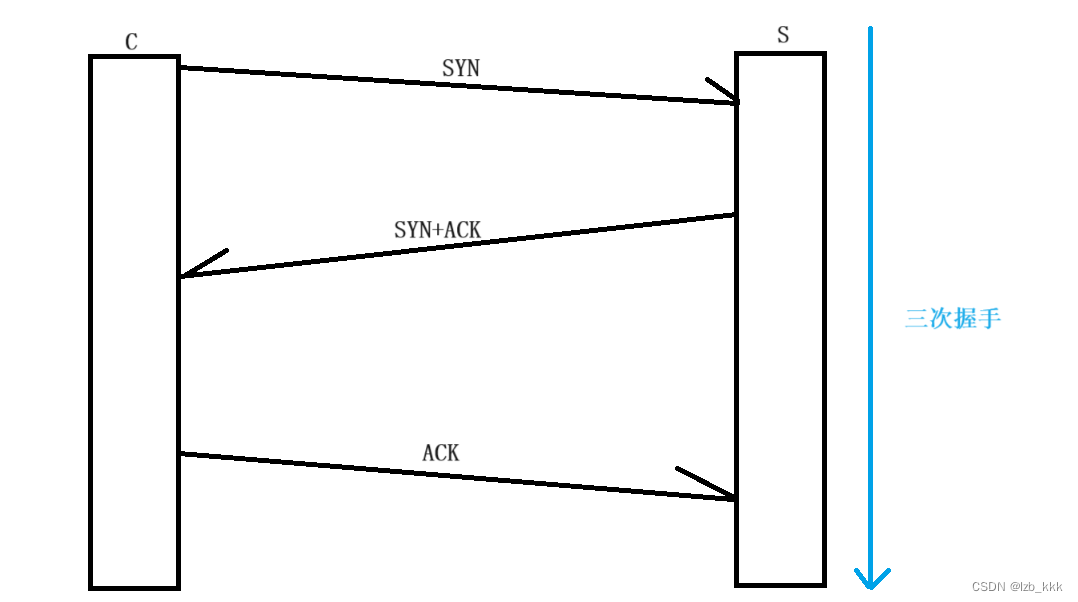
三次握手
TCP协议的相关机制
综上所述,我们可以总结出TCP协议的几个机制:
确认应答(ACK)机制
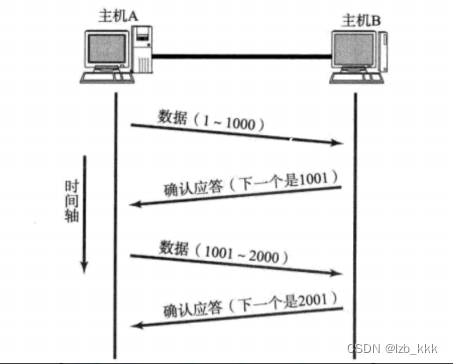
TCP将每个字节的数据都进行了编号,即为序列号,每个ACK都带有对应的确认序列号,意思是告诉发送者,我已经收到了哪些 数据,下次你从哪里开始发
超时重传机制
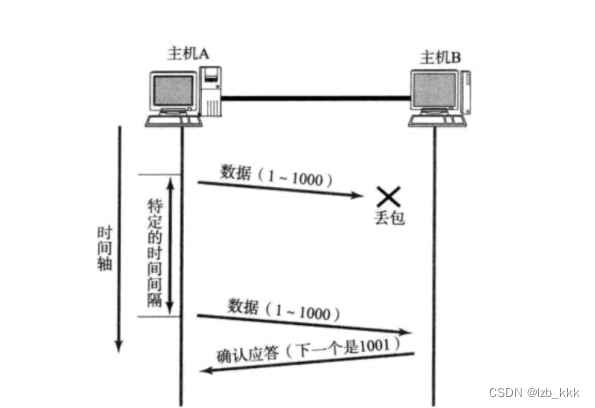
- 主机A发送数据给B之后,可能因为网络拥堵等原因,数据无法到达主机B;
- 如果主机A在一个特定时间间隔内没有收到B发来的确认应答,就会进行重发。
但是主机A未收到B的确认应答,也可能是ACK丢失了。

那么超时的时间,也就是这个特定的时间间隔是怎么确定的呢?
- 最理想的情况下, 找到一个最小的时间, 保证 "确认应答一定能在这个时间内返回".
- 但是这个时间的长短, 随着网络环境的不同, 是有差异的.
- 如果超时时间设的太长, 会影响整体的重传效率;
- 如果超时时间设的太短, 有可能会频繁发送重复的包
TCP为了保证无论在任何环境下都能比较高性能的通信, 因此会动态计算这个最大超时时间.
- Linux中(BSD Unix和Windows也是如此), 超时以500ms为一个单位进行控制, 每次判定超时重发的超时 时间都是500ms的整数倍.
- 如果重发一次之后, 仍然得不到应答, 等待 2*500ms 后再进行重传.
- 如果仍然得不到应答, 等待 4*500ms 进行重传. 依次类推, 以指数形式递增.
- 累计到一定的重传次数, TCP认为网络或者对端主机出现异常, 强制关闭连接.
连接管理机制
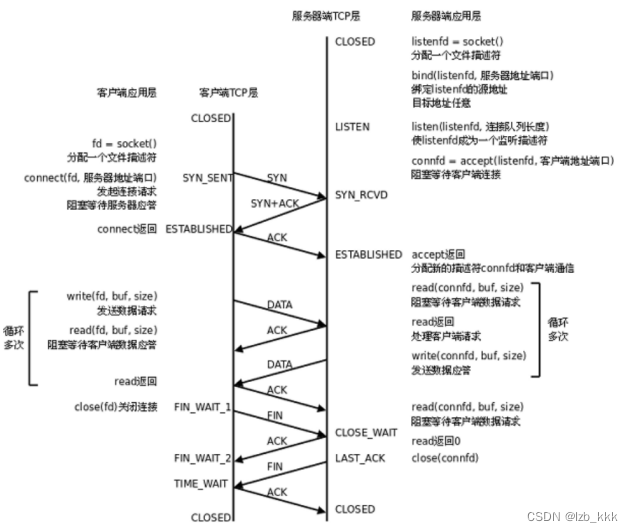
服务端状态转换
[CLOSED -> LISTEN] 服务器端调用listen后进入LISTEN状态,等待客户端连接。
[LISTEN -> SYS_RCVD] 一旦监听到连接请求(同步报文段SYN),就将该连接放入内核等待队列中,并向客户端发送SYN确认报文
[SYS_RCVD -> ESTABLISHED] 服务端一旦收到客户端的确认报文,就进入ESTABLISHED,可以进行读取数据
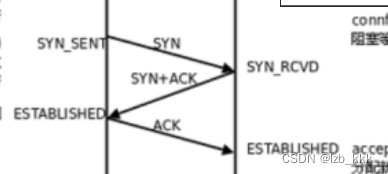
[ESTABLISHED -> CLOSE_WAIT] 当客户端主动关闭连接(调用close),服务器会收到结束报文段,服务器返回确认报文段并进入CLOSE_WAIT;

客户端状态转化
为什么采用三次握手?
一次的话容易受到SYN洪水攻击 ,两次的话连接失败的成本会嫁接到服务器上
四次挥手可以改成三次吗?
当发送关闭信号时,便不再发送数据,只发送一些ACK报文。
四次挥手过程如下:
1.客户端:我要关闭了 //第一次挥手
2.服务器:好的我知道了(ACK) //第二次挥手
3.此时服务器可能还有未发送完毕的正常业务数据,等发送完毕后再说:我要关闭了 //第三次挥手
4.客户端:好的我知道了 //第四次挥手
如果第三步服务器正好没有业务数据要发送了,可用捎带应答,实现三次挥手
PS:listen的第二个参数?backlog+1,表示底层已经建立好的连接队列的最大长度
全连接队列的大小为什么不能太长?
没必要太长 ,服务器没时间消耗连接时,还需要更多的内存来维护这个连接
为什么不能没有全连接队列?
因为如果没有全连接队列的话,一旦服务器当前资源空闲,上层无法快速补齐,导致服务器资源无法被充分消耗
一个网络报文在网络里存活的时间称为MSL
TIME_WAIT:等多长时间,为什么?
两个MSL即相当于一个报文的一来一回
- 让通信双方历史数据得以消散
- 让我们断开连接,4次挥手,具有较好的容错性
从客户端传送到服务端这个时间称为最大传送时长
报文在网络存在的时间称为最大存在时长
流量控制
- 接收端将自己可以接收的缓冲区大小放入 TCP 首部中的 "窗口大小" 字段, 通过ACK端通知发送端;
- 窗口大小字段越大, 说明网络的吞吐量越高;
- 接收端一旦发现自己的缓冲区快满了, 就会将窗口大小设置成一个更小的值通知给发送端;
- 发送端接受到这个窗口之后, 就会减慢自己的发送速度;
- 如果接收端缓冲区满了, 就会将窗口置为0; 这时发送方不再发送数据, 但是需要定期发送一个窗口探测数 据段, 使接收端把窗口大小告诉发送端
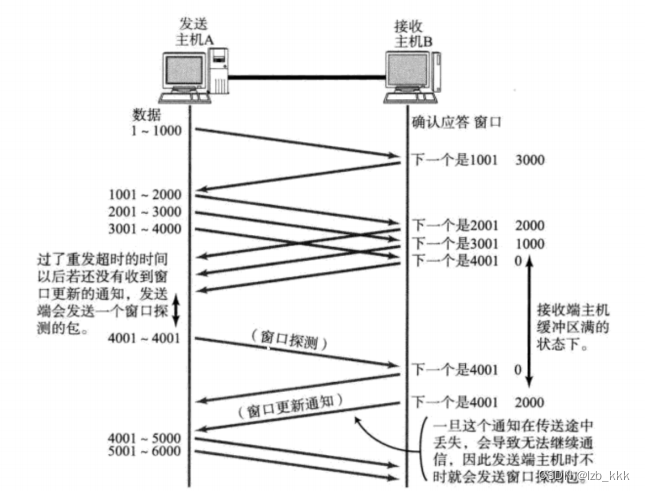
流量控制常见问题:
1.第一次发送数据的时候,怎么保证发送的数据量是合理的?
三次握手时,双方交换了报文,同时也协商了双方的接收能力。第三次握手的时候,可以携带数据,先识别ACK。前两次是不许携带数据。2.流量控制,属于可靠性,还是属于效率?属于可靠性,防止正常丢包,变相提高了效率
滑动窗口
滑动窗口是我们发送端缓冲区的一部分。至于区域划分可以理解成通过双指针(下标)进行区分即可。
滑动窗口的大小,不能超过对方的接收缓冲区的剩余空间的大小,即应答报文的窗口大小
情况1:如果丢包了,怎么理解滑动窗口

如果我们成功发送2001之前的报文,也得到了接收方返回的ACK报文,3001位置发生丢包,4001,5001得到了接收方返回的ACK报文,我们在进行窗口滑动时,会在2001位置停下来,等待3001位置进行重发得到ACK报文,在加上之前我们对确认序号的定义:确认序号是x,x之前的报文我们全部都收到了,综上保证了滑动窗口连续的向后更新,不会出现跳跃的情况,也就是跳过丢包的报文。
情况2:数据包直接丢了
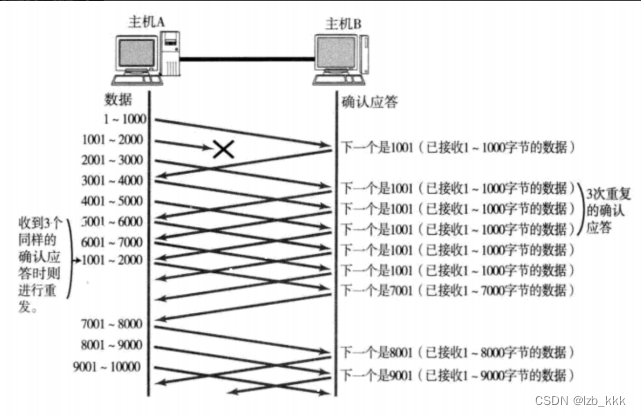
发送方连续三次收到同样的确认应答时则进行重发,这种方式称为快重传 。
已经有了快重传,为什么还要有超时重传?
快重传是有条件的,连续三次收到同样的确认应答才进行快重传,如果后面没有那么多数据发送,就不会触发快重传,因此快重传是提高效率的,超时重传相当于是兜底的。
问题2:滑动窗口可以向左移动吗?会向右移动吗?移动的时候,大小会变化吗?怎么变化?会为0吗?
不可以向左移动,因为滑动窗口本身划分的数据区域左侧是已经发送已经确认的。
右不变,做移动,范围缩小,左右都移动,范围扩大;
移动的时候,大小会动态变化
如果为0,发送方会进行窗口探测,如下进行更改大小
滑动窗口 start = 根据确认序号设置
end=确认序号+min(窗口大小,有效数据区域大小)
因此流量控制是通过滑动窗口实现的,通过控制滑动窗口大小
问题3:滑动窗口会在发送缓冲区越界吗?
不会,tcp采用了类似环状的算法
拥塞控制
如果发送数据,出现问题,不仅仅是对方主机出现问题,也有可能是网络出现问题
- 如果通信的时候,出现少量的丢包(常规情况)
- 如果通信的时候,出现大量的丢包(网络出现了问题)
- 硬件设备出现问题
- 数据量太大,引起阻塞
如果通信双方出现了大量的数据丢包问题(滑动窗口内大量的数据都超时了),tcp会判断网络出现问题了(网络拥塞了)
我们发送方应该怎么办?我们不能立即对报文进行超时重发,否则会加重网络拥塞。
延迟应答
- 假设接收端缓冲区为1M. 一次收到了500K的数据; 如果立刻应答, 返回的窗口就是500K;
- 但实际上可能处理端处理的速度很快, 10ms之内就把500K数据从缓冲区消费掉了;
- 在这种情况下, 接收端处理还远没有达到自己的极限, 即使窗口再放大一些, 也能处理过来;
- 如果接收端稍微等一会再应答, 比如等待200ms再应答, 那么这个时候返回的窗口大小就是1M;
- 数量限制: 每隔N个包就应答一次;
- 时间限制: 超过最大延迟时间就应答一次;
面向字节流
- 调用write时, 数据会先写入发送缓冲区中;
- 如果发送的字节数太长, 会被拆分成多个TCP的数据包发出;
- 如果发送的字节数太短, 就会先在缓冲区里等待, 等到缓冲区长度差不多了, 或者其他合适的时机发送出去;
- 接收数据的时候, 数据也是从网卡驱动程序到达内核的接收缓冲区;
- 然后应用程序可以调用read从接收缓冲区拿数据;
- 另一方面, TCP的一个连接, 既有发送缓冲区, 也有接收缓冲区, 那么对于这一个连接, 既可以读数据, 也可以写数据. 这个概念叫做 全双工
- 写100个字节数据时, 可以调用一次write写100个字节, 也可以调用100次write, 每次写一个字节;
- 读100个字节数据时, 也完全不需要考虑写的时候是怎么写的, 既可以一次read 100个字节, 也可以一次read一个字节, 重复100次;
粘包问题
面向字节流衍生出来的问题,接收一个半或者半个(不完整的报文);
如何解决用户层的粘包问题?
- 定长报文:在应用层通过自定义协议,明确报文和报文之间的边界
- 使用特殊字符
- 使用自描述字段+定长报头
- 使用自描述字段+特殊字符
对于UDP协议来说, 是否也存在 "粘包问题" 呢?
- 对于UDP, 如果还没有上层交付数据, UDP的报文长度仍然在. 同时, UDP是一个一个把数据交付给应用层. 就有很明确的数据边界.
- 站在应用层的站在应用层的角度, 使用UDP的时候, 要么收到完整的UDP报文, 要么不收. 不会出现"半个"的情况。
TCP异常情况
1)进程终止
连接正常自动断开,因为tcp连接是和文件直接相关的,文件的生命周期是随进程的。
2)机器重启
先杀掉所有的进程
3)机器掉电/网线断开
