安徽创誉建设工程有限公司网站湖南常德属于哪个市
Rest微服务工程搭建---学习笔记2/9
- 1、简单架构示意图
- 2、创建Cloud-provider-payment8001 微服务提供者Module模块
- 2.1. 建Module
- 2.2. 改pom
- 2.3. 写yml
- 2.4. 主启动
- 2.5. 业务类
- 3、创建Cloud-consumer-order80 微服务消费者订单Module模块
- 3.1. 建Module
- 3.2. 改pom
- 3.3. 写yml
- 3.4. 主启动
- 3.5. 业务类
- 4、工程重构
- 4.1 新建一个 cloud-api-commons 子模块
- 4.2 mvn跳过test,mvc clean,mvn install
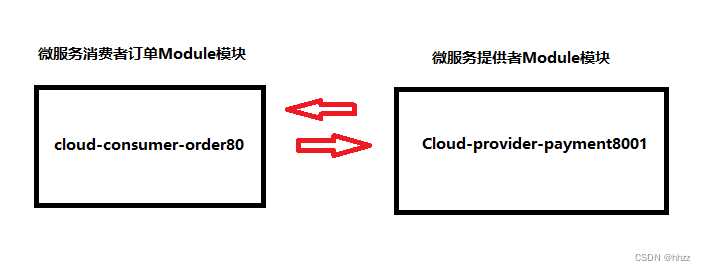
1、简单架构示意图
两个模块,一个是服务提供者模块,另一个是服务消费者模块
2、创建Cloud-provider-payment8001 微服务提供者Module模块
2.1. 建Module
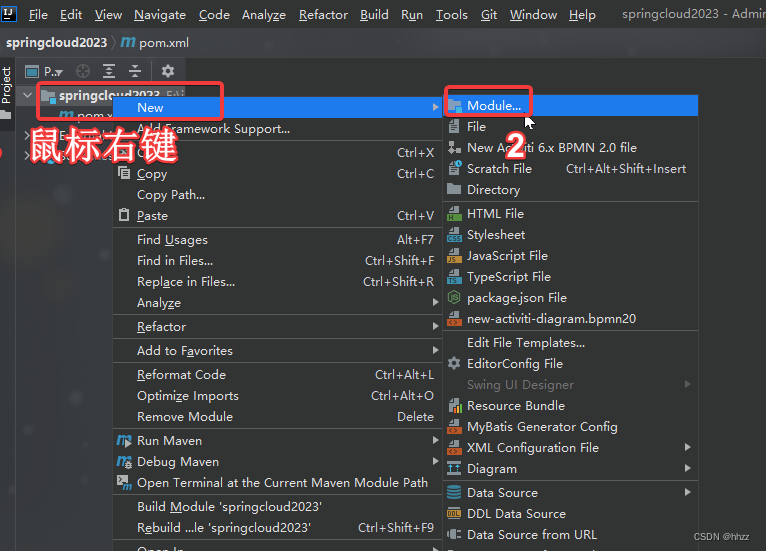
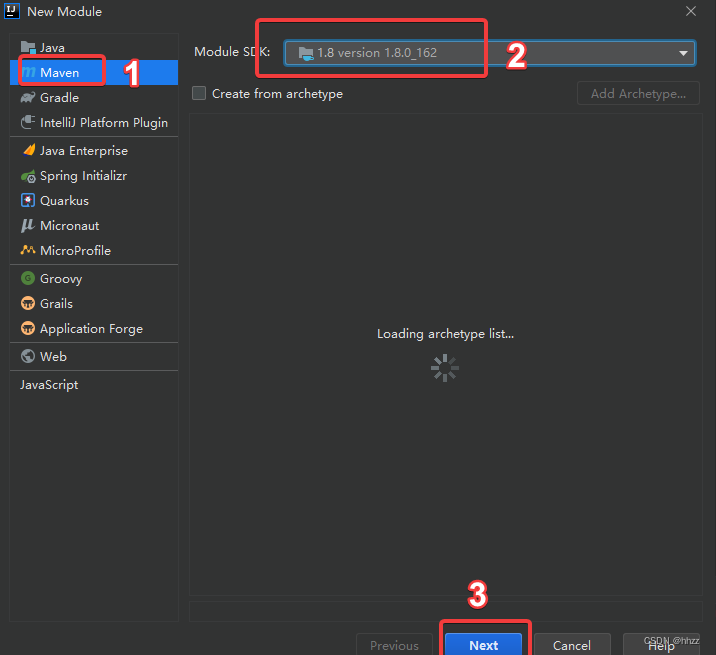
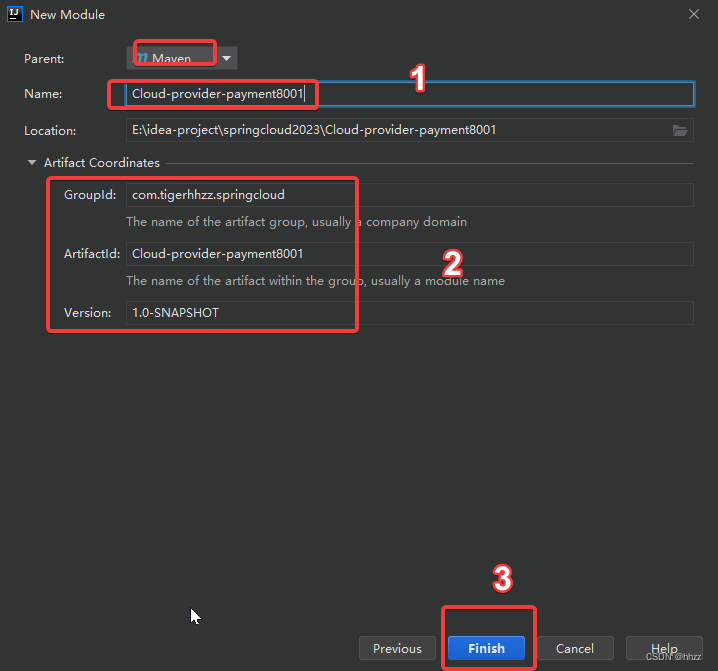
创建完成后回到父工程查看pom文件变化
<?xml version="1.0" encoding="UTF-8"?><project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"><modelVersion>4.0.0</modelVersion><groupId>com.tigerhhzz.springcloud</groupId><artifactId>springcloud2023</artifactId><version>1.0-SNAPSHOT</version><modules><module>Cloud-provider-payment8001</module></modules><packaging>pom</packaging><name>Maven</name><!-- FIXME change it to the project's website --><url>http://maven.apache.org/</url><inceptionYear>2001</inceptionYear><distributionManagement><site><id>website</id><url>scp://webhost.company.com/www/website</url></site></distributionManagement><!-- 统一管理jar包版本 --><properties><project.build.sourceEncoding>UTF-8</project.build.sourceEncoding><maven.compiler.source>1.8</maven.compiler.source><maven.compiler.target>1.8</maven.compiler.target><junit.version>4.13.2</junit.version><log4j.version>1.2.17</log4j.version><lombok.version>1.18.26</lombok.version><mysql.version>8.0.32</mysql.version><druid.version>1.2.16</druid.version><mybatis.spring.boot.version>3.0.1</mybatis.spring.boot.version></properties><!-- 1、只是声明依赖,并不实际引入,子项目按需声明使用的依赖 --><!-- 2、子项目可以继承父项目的 version 和 scope --><!-- 3、子项目若指定了 version 和 scope,以子项目为准 --><dependencyManagement><dependencies><!--spring boot 2.2.2--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-dependencies</artifactId><version>3.0.5</version><type>pom</type><scope>import</scope></dependency><!--spring cloud Hoxton.SR1--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-dependencies</artifactId><version>2022.0.2</version><type>pom</type><scope>import</scope></dependency><!--spring cloud alibaba 2.1.0.RELEASE--><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-alibaba-dependencies</artifactId><version>2021.0.4.0</version><type>pom</type><scope>import</scope></dependency><dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>${mysql.version}</version></dependency><dependency><groupId>com.alibaba</groupId><artifactId>druid</artifactId><version>${druid.version}</version></dependency><dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>${mybatis.spring.boot.version}</version></dependency><dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>${junit.version}</version></dependency><dependency><groupId>log4j</groupId><artifactId>log4j</artifactId><version>${log4j.version}</version></dependency><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><version>${lombok.version}</version><optional>true</optional></dependency></dependencies></dependencyManagement><build><plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId><configuration><fork>true</fork><addResources>true</addResources></configuration></plugin></plugins></build></project>2.2. 改pom
修改本模块的pom文件如下:
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"><parent><artifactId>springcloud2023</artifactId><groupId>com.tigerhhzz.springcloud</groupId><version>1.0-SNAPSHOT</version></parent><modelVersion>4.0.0</modelVersion><artifactId>Cloud-provider-payment8001</artifactId><properties><maven.compiler.source>8</maven.compiler.source><maven.compiler.target>8</maven.compiler.target></properties><dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><!--这个和web要写到一块--><artifactId>spring-boot-starter-actuator</artifactId></dependency><dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId></dependency><dependency><groupId>com.alibaba</groupId><artifactId>druid-spring-boot-starter</artifactId><version>1.1.10</version></dependency><!--mysql-connector-java--><dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId></dependency><!--jdbc--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-jdbc</artifactId></dependency><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><scope>test</scope></dependency></dependencies></project>
2.3. 写yml
编写application.yml配置文件
server:port: 8001spring:application:name: cloud-provider-payment8001datasource:type: com.alibaba.druid.pool.DruidDataSourcedriver-class-name: com.mysql.jdbc.Driverurl: jdbc:mysql://localhost:3306/springcloud-tigerhhzz?useUnicode=true&characterEncoding=utf-8&useSSL=falseusername: rootpassword: 123456
mybatis:mapper-locations: classpath:mapper/*.xmltype-aliases-package: com.dkf.springcloud.entities # 所有Entity 别名类所在包热部署:这里我使用的Jrebel插件。
2.4. 主启动
package com.tigerhhzz.springcloud;import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;/*** @author Administrator*/
@SpringBootApplication
public class PaymentMain8001 {public static void main(String[] args){SpringApplication.run(PaymentMain8001.class, args);}
}
2.5. 业务类
下面的常规操作:
- 建表SQL
create table `payment`(`id` bigint(20) not null auto_increment comment 'ID',`serial` varchar(200) default '',PRIMARY KEY (`id`))ENGINE=InnoDB AUTO_INCREMENT=1 DEFAULT CHARSET=utf8select * from payment;
entities
import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;import java.io.Serializable;@Data //set/get方法
@AllArgsConstructor //有参构造器
@NoArgsConstructor //无参构造器
public class Payment implements Serializable {private long id;//数据库是bigintprivate String serial;
}
通用结果返回类实体:
import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;//返回给前端的通用json数据串
@Data //set/get方法
@AllArgsConstructor //有参构造器
@NoArgsConstructor //无参构造器
public class CommonResult<T> {private Integer code;private String message;private T data; //泛型,对应类型的json数据//自定义两个参数的构造方法public CommonResult(Integer code, String message){this(code, message, null);}
}
dao
@Mapper // 是ibatis下面的注解 //@Repositoty有时候会有问题
public interface PaymentDao {int create(Payment payment);Payment getPaymentById(@Param("id") Long id);
}
resource下创建mapper文件夹,新建PaymentMapper.xml。在yml里有所有entity别名类所在包,所有payment不用写全类名
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis-3-mapper.dtd" >
<mapper namespace="com.tigerhhzz.springcloud.dao.PaymentDao"><resultMap id="BaseResultMap" type="com.tigerhhzz.springcloud.entities.Payment"><id column="id" property="id" jdbcType="BIGINT"/><id column="serial" property="serial" jdbcType="VARCHAR"/></resultMap><insert id="create" parameterType="Payment" useGeneratedKeys="true" keyProperty="id">insert into payment(serial) values (#{serial})</insert><select id="getPaymentById" parameterType="Long" resultMap="BaseResultMap">select * from payment where id = #{id}</select>
</mapper>
@Param注解
service
public interface PaymentService {int create(Payment payment);Payment getPaymentById(@Param("id") Long id);
}
@Service
public class PaymentServiceImpl implements PaymentService {@Autowiredprivate PaymentDao paymentDao;@Overridepublic int create(Payment payment) {return paymentDao.create(payment);}@Overridepublic Payment getPaymentById(Long id) {return paymentDao.getPaymentById(id);}
}
controller
@RestController //必须是这个注解,因为是模拟前后端分离的restful风格的请求,要求每个方法返回 json
@Slf4j
public class PaymentController {@Resourceprivate PaymentService paymentService;@PostMapping(value = "/payment/create")// 注意这里的 @RequestBody 是必须要写的,虽然 MVC可以自动封装参数成为对象,// 但是当消费者项目调用,它传参是 payment 整个实例对象传过来的, 即Json数据,因此需要写这个注解public CommonResult create(@RequestBody Payment payment){int result = paymentService.create(payment);log.info("****插入结果:" + result);if(result > 0){return new CommonResult(200, "插入数据库成功", result);}return new CommonResult(444, "插入数据库失败", null);}@GetMapping(value = "/payment/{id}")public CommonResult getPaymentById(@PathVariable("id")Long id){Payment result = paymentService.getPaymentById(id);log.info("****查询结果:" + result);if(result != null){return new CommonResult(200, "查询成功", result);}return new CommonResult(444, "没有对应id的记录", null);}
}
启动8001模块

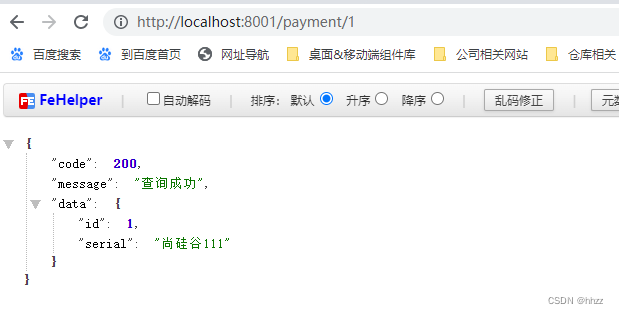
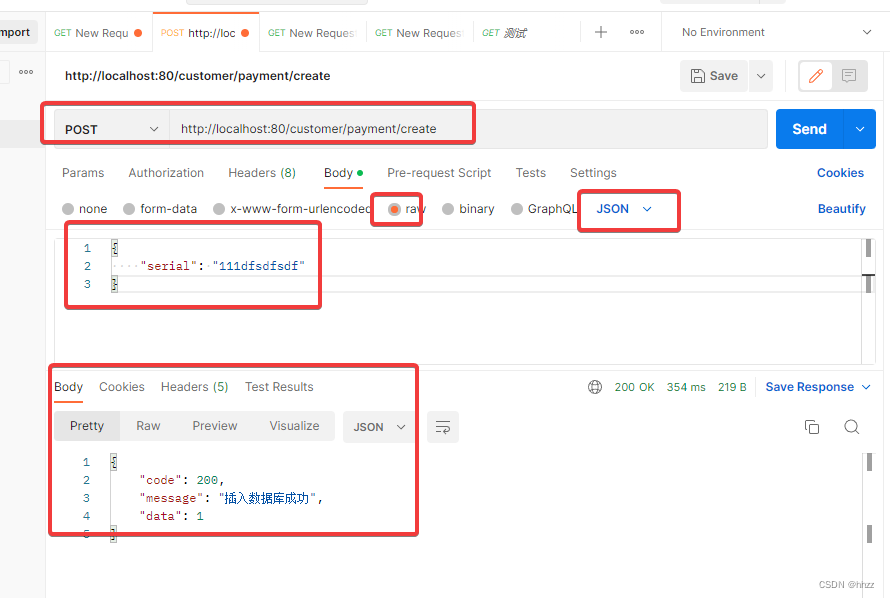
对应POST方式的请求,要学会用POSTMAN工具
测试插入一条数据
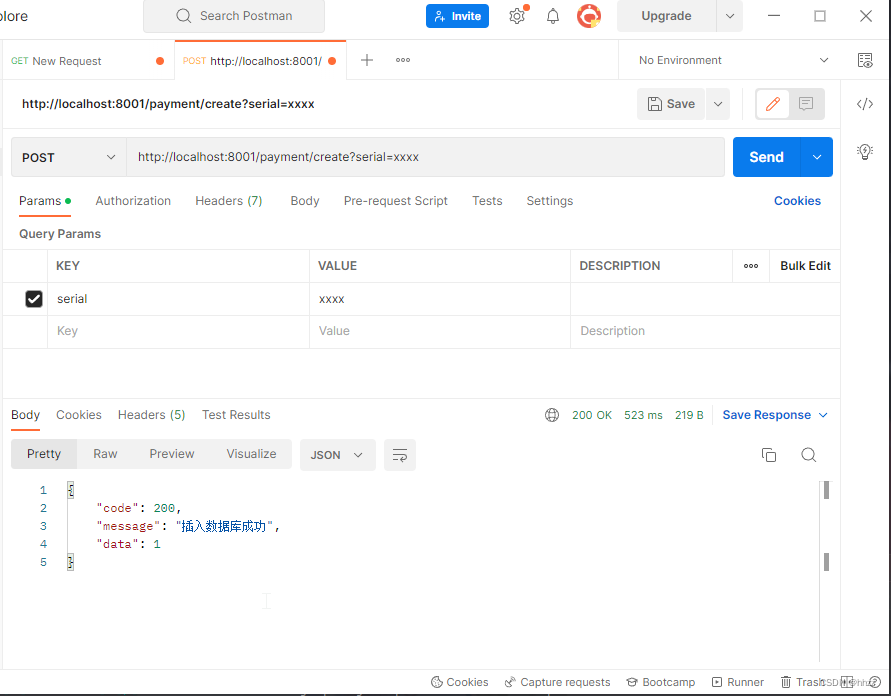
微服务多了之后就使用run dashboard
不但编译有个别地方会报错,启动也会报错,但是测试两个接口都是没问题的,推测启动报错是因为引入了下面才会引入的jar包,目前不影响。
3、创建Cloud-consumer-order80 微服务消费者订单Module模块
3.1. 建Module
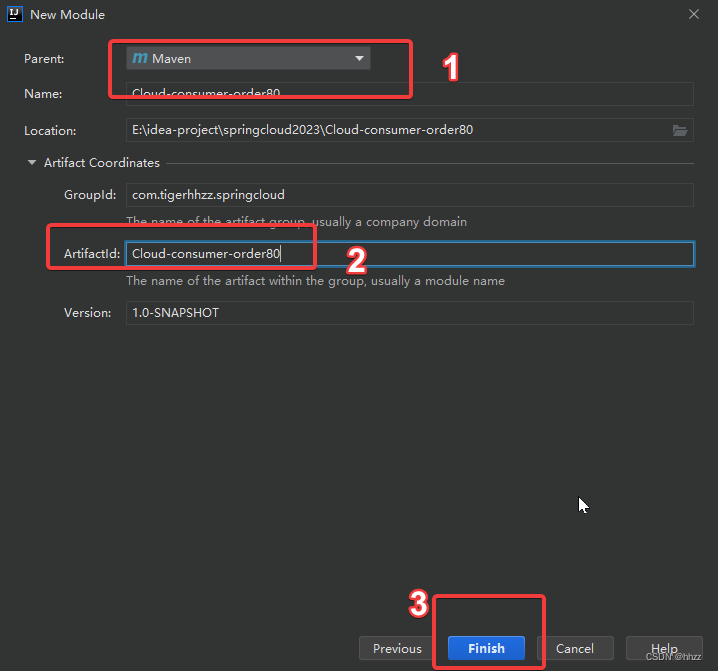
3.2. 改pom
修改本模块的pom文件如下:
3.3. 写yml
编写application.yml配置文件
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"><parent><artifactId>springcloud2023</artifactId><groupId>com.tigerhhzz.springcloud</groupId><version>1.0-SNAPSHOT</version></parent><modelVersion>4.0.0</modelVersion><artifactId>Cloud-consumer-order80</artifactId><properties><maven.compiler.source>8</maven.compiler.source><maven.compiler.target>8</maven.compiler.target></properties><dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-actuator</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional></dependency><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional></dependency><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-test</artifactId><scope>test</scope></dependency></dependencies></project>
3.4. 主启动
OrderMain80.java
package com.tigerhhzz.springcloud;import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;@SpringBootApplication
public class OrderMain80{public static void main(String[] args){SpringApplication.run(OrderMain80.class,args);}
}
3.5. 业务类
entites包中的类也拷贝到本项目中
entities/CommonResult.java
entities/Payment.java
配置RestTemplate
ApplicationContextConfig 内容:
package com.tigerhhzz.springcloud.config;import org.springframework.context.annotation.Bean;
import org.springframework.context.annotation.Configuration;
import org.springframework.web.client.RestTemplate;/*** @author tigerhhzz* @date 2023/4/8 22:52*/
@Configuration
public class ApplicationContextConfig {@Beanpublic RestTemplate getRestTemplate(){return new RestTemplate();/*RestTemplate提供了多种便捷访问远程http服务的方法,是一种简单便捷的访问restful服务模板类,是spring提供的用于rest服务的客户端模板工具集*/}
}
controller
package com.tigerhhzz.springcloud.controller;import com.tigerhhzz.springcloud.entities.CommonResult;
import com.tigerhhzz.springcloud.entities.Payment;
import lombok.extern.slf4j.Slf4j;
import org.springframework.web.bind.annotation.GetMapping;
import org.springframework.web.bind.annotation.PathVariable;
import org.springframework.web.bind.annotation.PostMapping;
import org.springframework.web.bind.annotation.RestController;
import org.springframework.web.client.RestTemplate;import javax.annotation.Resource;@RestController
@Slf4j
public class OrderController {//远程调用的 地址public static final String PAYMENY_URL = "http://localhost:8001";@Resourceprivate RestTemplate restTemplate;@PostMapping("customer/payment/create")public CommonResult<Payment> create (Payment payment){return restTemplate.postForObject(PAYMENY_URL + "/payment/create",//请求地址payment,//请求参数CommonResult.class);//返回类型}@GetMapping("customer/payment/{id}")public CommonResult<Payment> getPaymentById(@PathVariable("id")Long id){return restTemplate.getForObject(PAYMENY_URL + "/payment/" + id,//请求地址CommonResult.class);//返回类型}
}如果 runDashboard 控制台没有出来,右上角搜索 即可
运用spring cloud框架基于spring boot构建微服务,一般需要启动多个应用程序,在idea开发工具中,多个同时启动的应用
需要在RunDashboard运行仪表盘中可以更好的管理,但有时候idea中的RunDashboard窗口没有显示出来,也找不到直接的开启按钮
80调用8001服务测试成功:
4、工程重构
将两个微服务模块中公共的部分,例如实体类等放到新建的微服务公共模块中
上面 两个子项目,有多次重复的 导入 jar,和重复的 Entity 实体类。可以把 多余的部分,加入到一个独立的模块中,将这个模块打包,并提供给需要使用的 module
4.1 新建一个 cloud-api-commons 子模块
将 entities 包里面的实体类放到这个子模块中,也将 pom 文件中,重复导入的 jar包放到这个新建的 模块的 pom 文件中。如下
<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"><parent><artifactId>springcloud2023</artifactId><groupId>com.tigerhhzz.springcloud</groupId><version>1.0-SNAPSHOT</version></parent><modelVersion>4.0.0</modelVersion><artifactId>Cloud-api-commons</artifactId><dependencies><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional></dependency><!-- 这个是新添加的,之前没用到,后面会用到。关于这个hutool 是个功能强大的工具包,官网:https://hutool.cn/ --><dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.1.0</version></dependency></dependencies></project>
4.2 mvn跳过test,mvc clean,mvn install
将此项目打包 install 到 maven仓库。
将 提供者 和 消费者 两个项目中的 entities 包删除,并删除掉加入到 cloud-api-commons 模块的 依赖配置。
将 打包到 maven 仓库的 cloud-api-commons 模块,引入到 提供者 和 消费者的 pom 文件中,如下所示
<!-- 引入自己定义的api通用包 --><dependency><groupId>com.tigerhhzz.springcloud</groupId><artifactId>Cloud-api-commons</artifactId><version>1.0-SNAPSHOT</version><scope>compile</scope></dependency>
post测试插入数据成功