大连网站建设外贸wordpress首页文章
目录
- 笔记
- 后续的研究方向
- 摘要
- 引言
ParBFT: Faster Asynchronous BFT Consensus with a Parallel Optimistic Path
CCS 2023

笔记
后续的研究方向
摘要
为了减少异步拜占庭容错(BFT)共识的延迟和通信开销,通常会添加一条乐观的路径,Ditto和BDT是最先进的代表。这些协议首先尝试运行乐观路径,该路径通常适用于部分同步的BFT,并在良好的情况下保证良好的性能。如果乐观路径无法取得进展,这些协议会在超时后切换到悲观路径,以确保异步网络中的活跃性。这种设计主要依赖于对网络延迟Δ的准确估计来正确设置超时参数。Δ的错误估计可能导致过早或延迟切换到悲观路径,在这两种情况下都会损害协议的效率。
为了解决上述问题,我们提出了采用并行乐观路径的ParBFT。只要乐观路径的引导者没有故障,ParBFT就可以确保低延迟,而不需要精确估计网络延迟。我们提出了ParBFT的两种变体,即ParBFT1和ParBFT2,在延迟和通信之间进行权衡。ParBFT1同时启动两条路径,在故障引导器下实现了较低的延迟,但即使在良好的情况下也具有二次消息复杂性。ParBFT2在好的情况下通过延迟悲观路径来降低消息的复杂性,代价是在有故障的引导器下有更高的延迟。实验结果表明,ParBFT的性能优于Ditto或BDT。特别是当网络条件恶劣时,ParBFT可以通过乐观路径达成共识,而Ditto和BDT则存在路径切换问题,必须使用悲观路径才能取得进展。
引言
在过去的十年里,区块链[38,55,66]的日益普及使人们重新关注拜占庭容错(BFT)共识协议[34,65,67]。一般来说,BFT共识协议确保多个副本达成一致,即使其中一小部分副本可能表现得任意(称为拜占庭副本)[44]。BFT共识协议根据其时序假设大致可分为三类:同步协议、部分同步协议和异步协议。在这三类中,异步协议对不可预测的网络条件提供了最强的鲁棒性[27,37,50]。然而,由于性能原因,异步BFT协议很少在生产中部署[46]。更具体地说,与同步和部分同步的对等协议相比,异步BFT协议具有更高的延迟(更大的轮数)和更高的通信开销,即使在所有副本都没有故障并且网络状况良好的情况下也是如此。
为了弥补异步BFT的较差性能,许多工作引入了一种乐观路径[43,57],Ditto[33]和BDT[46]是最近的代表。在高层,这些协议通常有两条路径:由领导者驱动的乐观部分同步路径和异步工作的悲观路径。系统首先尝试运行乐观路径,该路径具有低延迟和较小的通信开销。如果乐观路径无法取得进展,则协议会在超时事件后返回到悲观路径。在悲观路径上的一个或多个协议实例之后,协议将切换回乐观路径。由于在任何给定时间只有一条路径被执行,我们将这种设计称为串行路径范式。
串行路径范例有几个缺点。首先,它需要对网络延迟(通常表示为Δ)进行良好的估计,以相应地设置计时器。正确地获得参数Δ是相当具有挑战性的。当领导者是拜占庭人时,乐观的道路无法取得任何进展,理想情况下应该尽快启动向悲观道路的后退。Δ的大值将延迟回退并损害延迟。相反,如果Δ被错误地设置得太小,超时和回退事件将提前触发,可能会干扰乐观道路上即将取得进展的无故障领导者。
此外,何时回到乐观的道路上也是一个艰难的决定。如果由于网络已经恢复,切换执行得太晚,则协议不必要地在悲观路径上停留太长时间。相反,在网络状况仍然不佳的情况下过于匆忙地切换回来是没有意义和浪费的,因为乐观的道路仍然无法取得进展。这甚至可能导致频繁的来回切换,使协议比简单地单独运行悲观路径更慢。在某些情况下,Ditto[33]选择了仓促的方法,并在悲观路径上的单个协议实例完成时执行切换。BDT[46]在其伪代码中同样使用了一个仓促切换。尽管BDT提到可以使用其他启发式方法进行切换,但设计这些启发式方法也是一项棘手的任务。
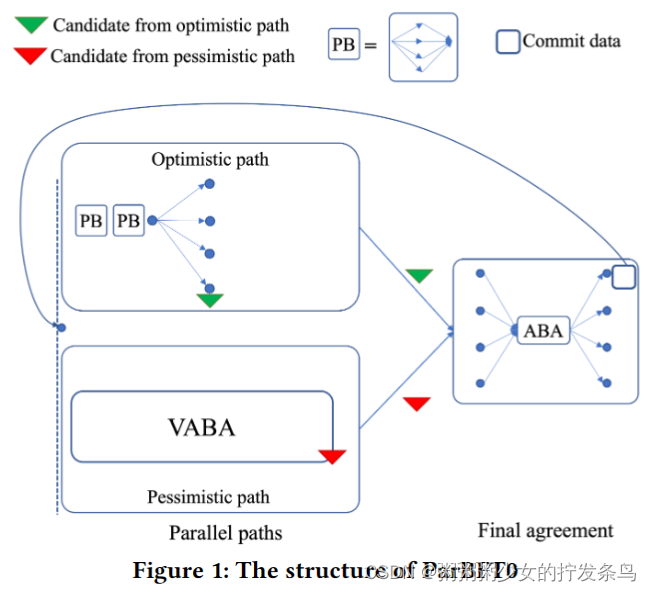
为了解决路径切换方面的这些挑战,我们提出了一种向异步BFT添加乐观路径的替代范式:并行运行这两条路径。在高级别上,通过并行运行这两条路径,副本可以在两条路径中的一条成功后立即做出决定。这使得协议能够优雅地处理好的和坏的网络条件,并避免串行路径模式的缺点。更具体地说,我们提出了并行运行部分同步乐观路径和异步悲观路径的ParBFT。这两条路径可以各自产生一个输出(称为候选)。然后,ParBFT利用异步二进制协议(ABA)算法在这两个候选者之间达成协议。ParBFT的最后一个关键设计元素是一种快捷机制:如果领导者没有故障,网络良好,所有副本都将在乐观路径的末尾决定,并直接前进到下一个实例,而不需要执行ABA算法,甚至不需要执行悲观路径。这使得ParBFT在良好情况下的性能类似于串行路径范式。
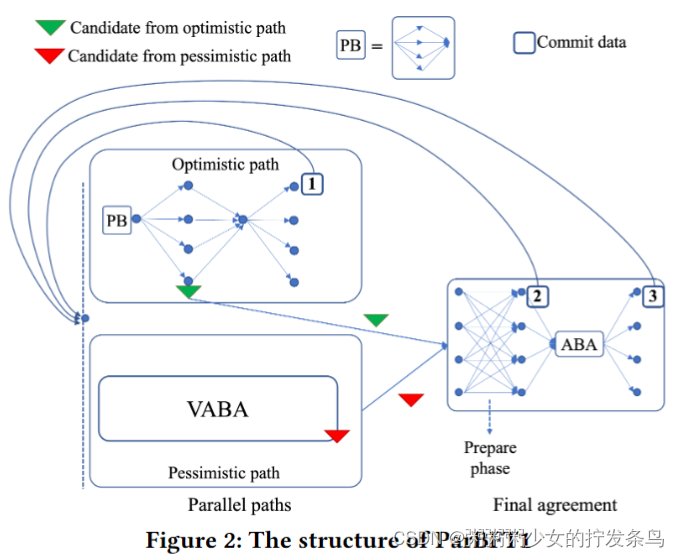
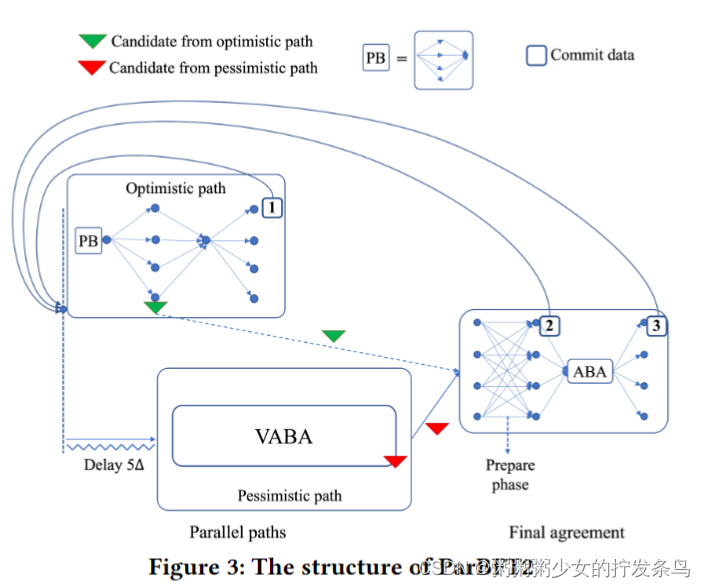
我们提出了ParBFT的两种变体,我们称之为ParBFT1和ParBFT2,它们在延迟和通信之间进行了权衡。ParBFT1同时启动这两条路径;这种变体在拜占庭领导人的领导下提供了更好的延迟,但即使在良好的情况下也会受到二次消息复杂性的影响。相反,ParBFT2延迟了悲观路径的启动,因此,在拜占庭领导人的领导下,以更高的延迟为代价,在良好的情况下将消息复杂性降低为线性。
如表1所示,Ditto[33]和BDT[46]之前的工作实现了5的低延迟𝛿(𝛿表示实际网络延迟),并且参数Δ被正确估计时(即。,𝛿 ≤Δ)。相比之下,ParBFT1和ParBFT2实现了5的良好延迟𝛿只要乐观路径的领导者是非错误的,无论Δ是否被正确估计。如前所述,在良好的情况下,ParBFT1牺牲了消息的复杂性:当领导者没有错误并且Δ的估计是正确的时,ParBFT 1会导致二次通信。ParBFT2通过将悲观路径的启动延迟5Δ时间来避免这个问题:这将在良好情况下的通信复杂性降低到𝑂(𝑡𝑛)1(𝑡和𝑛分别表示实际故障副本和总副本的数量),但在拜占庭领导人的领导下增加了该数量的延迟。
我们还注意到,虽然ParBFT1根本不需要参数Δ,但ParBFT2带回了Δ的参数。但与先前的工作不同,对Δ的错误估计的惩罚要小得多。具体来说,当Δ设置得太小时,即Δ<𝛿,ParBFT2只会增加通信成本,而之前的工作会产生更长的延迟、增加的通信成本以及来回切换的潜在问题。
我们实现了ParBFT的两种变体,并进行了广泛的实验,以评估其与先前工作相比的性能。我们的实现使用基于链的范式,其中不同的协议实例被流水线传输以提高吞吐量。实验分为三个部分,分别对应三种不同的场景。第一部分模拟了一个良好的情况,即领导者没有故障,网络良好。
在第二部分中,我们通过故意延迟消息来模拟慢速网络,同时假设一个没有故障的领导者。最后,在第三部分中,我们通过延迟领导者的建议来引入一个错误的领导者。
实验结果表明,在良好的情况下,ParBFT2的性能与Ditto和BDT相当好,因为所有三个协议都可以通过乐观路径提交。正如预期的那样,随着副本数量的增加,ParBFT1的性能由于其二次消息复杂性而恶化。在慢速网络的情况下,延迟设置为大于Δ,与Ditto和BDT相比,ParBFT1和ParBFT2表现出明显更低的延迟。ParBFT实现了更低的延迟,因为即使网络延迟估计错误,它也可以通过乐观路径提交,而Ditto或BDT必须切换到悲观路径。在一个错误的领导者的情况下,所有协议都将通过悲观路径提交。然而,ParBFT1提供了比Ditto、BDT和ParBFT2更低的延迟,因为它可以立即启动悲观路径,而无需等待超时事件。
综上所述,我们在本文中做出了以下贡献。我们首先确定了当前串行路径异步协议的主要局限性:它们依赖于对网络延迟的准确估计来在两条路径之间进行适当的切换。然后,我们提出了一种称为ParBFT的新范式,该范式并行运行两条路径以解决这些限制。提出了ParBFT的两种变体,在延迟和通信开销之间进行了权衡。最后,我们实现了我们的协议,并进行了全面的实验来展示它们的优势。