大学生做社交网站有哪些谷歌浏览器 安卓下载
注:本文缩写说明
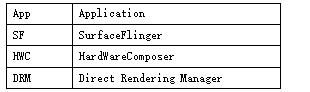
本文代码都是基于Android S
一、概述
本文将对从App画出一帧画面到这帧画面是如何到达屏幕并最终被人眼看到的这一过程进行简要分析,并将这其中涉及到的各个流程与其在systrace上的体现对应起来,期望最终能够让读者对Android系统下的画面显示流程有一个宏观的认识。
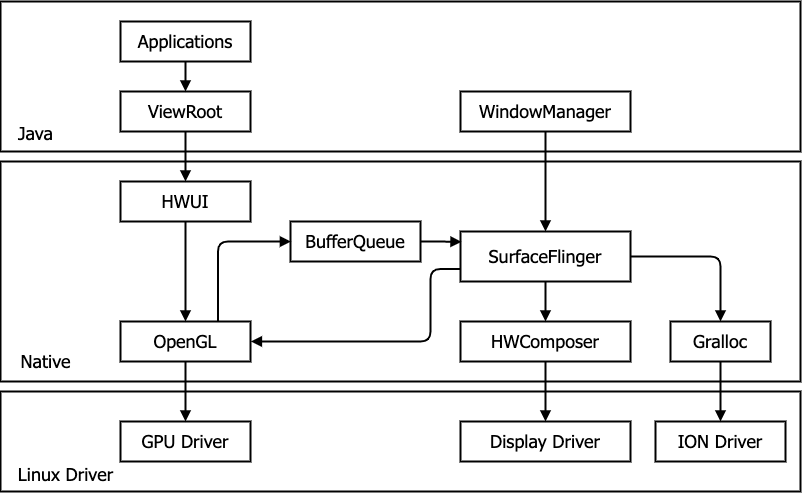
上图为Android的图形显示系统框架图,首先上层应用通过ViewRoot的scheduleTraversals函数发起绘制任务,并通过HWUI调用OpenGL接口将绘制数据传递给GPU处理;SF会接收所有应用更新的绘制数据,并根据Z-Order、透明度、大小、位置等参数计算出每个应用图层在最终合成图像中的位置;SF完成图层处理后会把所有的应用图层提供给HWC,由HWC来决定这些图层的合成策略并调用屏显驱动做合成;最后屏显驱动会将合成的最终画面送到硬件屏幕显示。
Android系统通过buffer缓冲区来保存图形信息,这个buffer的内存空间是有SF向图形内存分配器Gralloc申请的,而Gralloc是通过ION Driver从kernel中开辟出一块共享内存。在整个图形显示流程中,buffer缓冲区会在App、SF、HWC之间来回流转,本文将通过buffer的数据流向来详细阐述Android的画面显示过程。
二、App到SF
应用界面发生变化也就是view数据发生了变化,会引起ViewRootImpl的requestLayout调用,进而调用scheduleTraversals方法。scheduleTraversals方法内会先向消息队列发送一个同步屏障,然后执行Choreographer回调,注册CALLBACK_TRAVERSAL类型的监听。Choreographer在监听到下一次Vsync信号来了后,会执行mTraversalRunnable的run方法,该方法内会调用doTraversal方法,移除消息队列中的同步屏障,并通过performTraversals方法触发布局绘制流程。

Choreographer和Vsync是在Android 4.1上黄油计划中引入的两个重要元素,最初的Vsync信号是由硬件屏幕根据系统帧率以固定的频率(60/90/120fps)向系统发送的时间脉冲信号,Choreographer和SurfaceFlinger都会监听这个信号来做绘制和合成。后来为了进一步提升界面流畅性体验,Android 4.4上又引入了Vsync虚拟化,通过DispSyncThread把Vsync虚拟化成Vsync-app和Vsync-sf,Vsync-app和Vsync-sf之间有固定的时间偏移,各自分别掌控着App和SurfaceFlinger的工作节奏,他们一前一后保持着绘制任务的流水节奏。
当Choreographer监听到Vsync信号后会回调doFrame方法,该方法主要完成两件事情:确认当前帧执行的时间戳和渲染当前帧数据。渲染数据时会顺序执行输入(Input)、动画(Animation)、绘制(TRAVERSAL)、提交(Commit)这4种类型的回调函数,而在执行TRAVERSAL类型的callback方法时就会调用到上面提到的doTraversal下的performTraversals方法触发布局绘制流程。

下图的systrace展示了UI数据从App到SurfaceFlinger的处理流程。从systrace上可以看到应用端有两个线程UI Thread和Render Thread用于处理应用想要更新的UI数据,其中UI Thread通过Choreographer配合Vsync信号有节奏的控制应用的绘制任务,并将所有要绘图的信息以绘图指令的形式记录到DisplayList里同步给Render Thread,Render Thread则将UI Thread传递过来的绘图数据送到GPU去做渲染。一旦同步工作完成,UI Thread就可以继续等下一个Vsync-app信号的到来,接着做下一帧的绘制。
Render Thread在做GPU渲染之前还需要申请一块buffer缓冲区用于存储GPU渲染的数据,这个buffer是应用通过Surface接口的dequeueBuffer方法向BufferQueue申请的,拿到buffer之后应用会调用OpenGL接口将绘制指令传递给GPU进行渲染,然后再通过queueBuffer函数将保存有渲染数据的buffer提交到SF作图层处理。
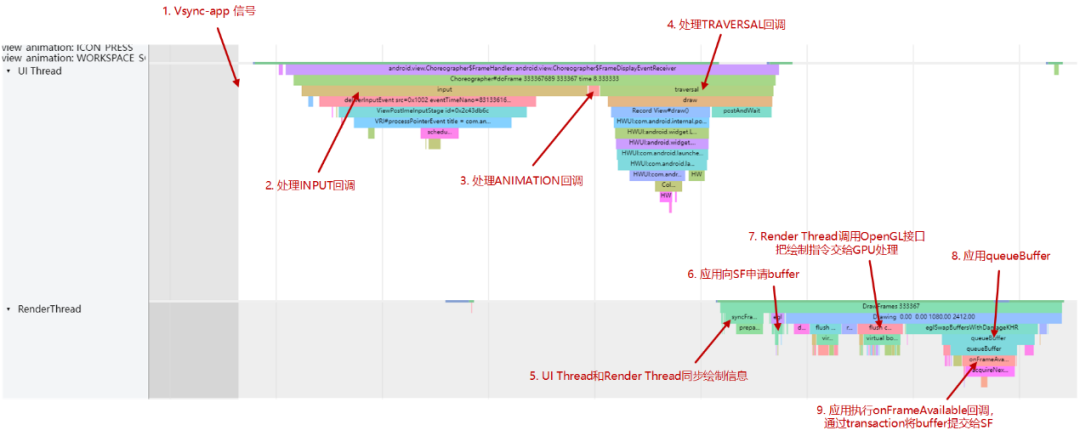
值得注意的是在Android S以前,buffer状态都是由BufferQueue进行管理,而bufferQueue是在SF中创建的,应用端的dequeue、queue Buffer操作都是通过binder和SF进行交互。但是在Android S上,BufferQueue的创建从SF中移出来,变成BLASTBufferQueue去完成BufferQueue的创建,dequeue、queue、acquire、release Buffer 的操作均由 App 进行。当App绘制完一帧后,会通过BLASTBufferQueue接口执行onFrameAvailable回调,并通过transaction事务将该buffer提交到SF。
三、SF到HWC
当SF监听到Vsync-sf信号就会调用onMessageReceived函数来处理UI数据。
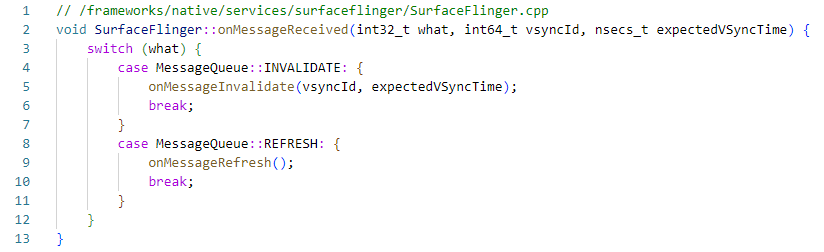
onMessageReceived方法主要是用来处理两个Message:
INVALIDATE消息 -- onMessageInvalidate首先会调用handleMessageTransaction方法检查Layer/Display的属性和数量是否有变化;然后调用handleMessageInvalidate方法检查每个Layer是否有新提交的buffer, 如果有则通过handlePageFlip调用latchBuffer方法将BufferQueue中的buffer通过acquireBuffer拿走;最后还会检查HWC是否有repaint请求。上述三种情况只要有一种发生了,refreshNeeded就会被置为true,onMessageRefresh方法就会被调用做图像合成。

REFRESH消息—onMessageRefresh方法则会对所有有buffer更新的Layer进行合成,大部分的合成工作是在present方法里完成的,这里SurfaceFlinger会和HWC进行交互,协同完成画面的合成。基本流程如下:
SF为HWC提供完整的Layer列表并通过chooseCompositionStrategy方法询问合成策略。
HWC根据硬件性能决定是使用硬件图层合成器还是GPU合成,并分别将每个Layer对应标记为overlay或GLES composition来进行响应。
需要硬件图层合成器合成的Layer直接由HWC处理,需要GPU合成的Layer则需要先由SF负责合成一个Layer后再和其他的Layer一起递交给HWC完成剩余的合成和显示。
当画面合成结束以后,SF还会调用postComposition做一些合成后的处理,其中就包括通过releaseBuffer释放SF在合成上一帧画面时拿到的所有buffer,以便应用在下次dequeueBuffer时能够拿到可用的buffer。

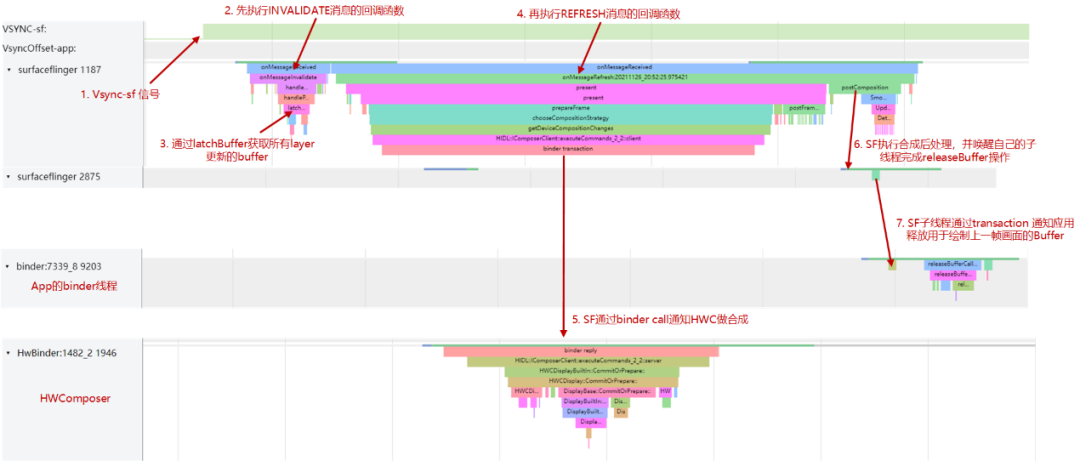
下图的systrace展示了UI数据从SF到HWC的处理流程。当SF监听到Vsync-sf信号后会顺序执行INVALIDATE和REFRESH消息的回调函数,在执行onMessageRefresh方法时,SF和HWC会协同选择合成策略,并由HWC完成最终的画面合成。画面合成完成后,SF会通过transaction事务通知应用释放用于绘制上一帧画面的buffer。
四、HWC到屏幕
systrace上看到的都是软件上的一些操作,无法看到硬件的处理流程。而UI数据从HWC到屏幕的这个阶段只有一小段时间是在软件上进行的,大部分时间都是硬件在处理数据。我们首先来看看该阶段软件上的主要工作,HWC是通过DRM向屏幕输出画面的,DRM是linux内核的一个子系统,用于负责与显卡交互,因此HWC会先通过drmModeAtomicCommit接口向kernel提交Layer数据,drmModeAtomicCommit通过ioctl调用到kernel,然后通知disp thread也就是下图中所示的crtc_commit线程调用complete_commit函数完成剩下的合成工作。

crtc_commit线程执行complete_commit方法时几乎一直处于D状态,表明此时DRM内的硬件正在做合成工作。经过一系列合成处理后最终的画面会通过DSI接口送到屏幕显示。至此,UI数据就完成了从应用端到硬件屏幕的旅程。
五、总结
一个buffer从被应用dequeue到最后HWC完成画面合成后由SF release的整个生命周期经历了如下流程:
Vsync-app信号到达后,APP端由Choreographer顺序执行Input、Animation和Traversal的回调,然后通过dequeueBuffer拿到一个可用的buffer开始绘图,再通过queueBuffer将包含绘图数据的buffer提交到SF。
Vsync-sf信号到达后,SF首先通过aquireBuffer获取所有Layer更新的buffer,然后根据Z-Order、透明度、大小、位置等参数对这些Layer进行图层处理,接着将所有的Layer送到HWC做合成。
HWC对多个Layer做合成,合成完成后通过libdrm提供的接口通知DRM模块把图像显示到屏幕。
最终的画面送到屏幕后,HWC会将用完的buffer还给SF,SF会在下一个Vsync-sf信号到达后release被归还的buffer。
本文以UI数据在显示系统中的数据流向为指引,依次分析了App、SF、HWC和硬件屏幕处理UI数据的基本步骤。Android显示系统十分复杂,涉及模块较多,并且随着时间的推移也在不断更新优化,但是其处理UI数据的基本流向不会变,本文旨在帮助读者对显示系统有一个宏观的认识,其中的一些处理细节还需要读者通过阅读源码慢慢领会。
参考资料:
1.Android源码:https://cs.android.com/android/platform/superproject
2.Android图形系统篇总结:https://www.jianshu.com/p/180e1b6d0dcd
3.Android Systrace 基础知识:https://www.androidperformance.com/2019/05/28/Android-Systrace-About/

长按关注内核工匠微信
Linux内核黑科技| 技术文章 | 精选教程
