台州专业网站设计系统报告怎么写
有一种打工人的羡慕,叫做“大厂”。
真是年少不知大厂香,错把青春插稻秧。
但是,在深圳有一群比大厂员工更庞大的群体,他们顶着大厂的“名”,做着大厂的工作,还可以享受大厂的伙食,却没有大厂的“命”。他们就是大厂的“外包员工”。
什么都做了,和什么都没做其实是一样的,走出“瞎忙活”的安乐窝,才是避开弯路的最佳路径。希望我的经历能帮助到有需要的朋友。

外包公司的特点有哪些?
首先,特点就是人员流动性特别大,接着上面例子,因为可能干了三四个月,该项目做完了,这10个人估计都得走,然后这10个人又会被外包公司派去其他的甲方公司面试,面试成功才有工资拿,没面试成功只有底薪2200。
如果一个外包人员面试甲方公司,一直都没有面试通过,那他就是只能一直拿底薪,大约每天70块钱的收入,所以,有些就觉得没劲,干脆辞职。
还有一个就是:你如果要入职外包公司的话,一般要经过两面,一面外包,过了外包的面试,才有第二轮甲方公司的面试,这些外包的人事都会提前通知你,去哪个甲方公司面试,然后第二面你又要去甲方面试,如果这个甲方公司面试通过了,就会给你发offer,让你入职签合同,如果第一个甲方公司面试没通过,那就去第二个甲方公司,依次类推,直到你面试的甲方公司通过才可以入职签合同。
关于签合同和福利待遇
薪酬福利
一般而言外包员工的薪酬福利是远低于正式员工的
正式员工:薪资之外还有五险一金和公司福利等;而外包的价格顶多是岗位的正常薪资。
职业发展
外包员工很快会遇到瓶颈,因为只有非核心岗位会外包,这类岗位缺乏长期发展的空间。
正式员工,有成绩或者呆的年限够长都回有相应的回报。
工作稳定性
外包是灵活用工的一种,意味着公司一旦需要裁员,首先考虑的是外包员工。
正式员工,会相对稳定,裁员,会获得法律的相应补偿。
合同签订
外包员工的合同,是和第三方外包公司签订。
正式员工的合同,是直接和公司签订。
工作范围
外包公司,一般是一对多,同时服务多家企业。
正式员工,一般是一对一,只服务于所在公司。
外包公司可不可以进呢?
一般情况下,我不建议大家选择去外包公司,因为从各个方面综合比较,外包公司都是不利于我们发展的。但是外包公司的存在又是大多数,我们应该怎么办呢?我的建议是,根据自身情况做“符合事实的选择”,如果我们找了很久的工作都没有拿到一份满意的offer,无论是心理还是身体上都承受不住这种煎熬,那么我们可以暂且先在外包公司进行工作,从而积累工作经验,等到时机继续寻找符合自己的满意公司。
但是在外包公司工作一定不要超过两年,要提前去策划自己如何跳出这个环境,从而找到更加有发展潜力的平台进行学习和发展。这些都是需要自己去运营的。在整个过程中,“学习”是主要改变的方式,通过巩固和学习技术与知识,我们可以增加自身的竞争力,毕竟我们还是做的技术行业,还是要用自身的技术能力来说话。
我的外包测试收获
在外包公司也不一定全无收获,我在外包公司这几年也收获不少,感慨良多!
技术方面
熟悉了大厂的流程,掌握各种工具
掌握了新的技术栈,如mysql都是在外包的这两年学习的
代码习惯更好了,
编程思想上的提升
问题定位速度的提升。
工作能力方面
更有耐心了,同事之间的交流也是很有礼貌
更能抗压了,有时候测试压力挺大的,只能多加班,有时候一个月工作日都在加班,最少每个月有15天的加班
更有效率了,简单的东西有时候很快就可以完成
生活方面
体重增加,因为伙食好了,现在早晚餐都包了,另外运动少了,基本没什么运动。
下一份工作不想做外包了
我之所以做了外包,是因为那时候刚来深圳,又没有找到合适的工作,就想先做一年看看,没想到这一做就是两年多,时间真的过的很快,不管是有意义的过还是颓废的过,都一样的快。
自动化测试学习建议
1、多样化练习
完全按照视频里的操作方法,用视频里的网站,按部就班的写代码,效果不大,并不是说没有必要。因为课程里所使用的网站都是老师“精心挑选”的,主要针对某个模块某个知识点而来的,用来做例子的功能也是最简单,主要目的是让学员明白当前所讲的知识点。
但是在实际应用的过程中肯定会比这复杂。所以建议在按照视频里的例子练习完成后,多拿一些常用的网站或者工作中正在使用的网站多做练习,这样我们往往会获取到一些课程里没有的知识。
一开始不会没关系,就是照着现有脚本抄也要练习,因为只有练习才能熟能生巧。
2、虚心学习不自以为是
因为我之前是有代码基础的,所以在第一次学习的过程中将所有代码相关的课程都跳过了,所以导致了知识的断层。第二次学习的过程中,是将课程从头到尾的完整的看了一遍并进行了实际操作,才发现,之前被我跳过的内容隐藏了一些我从前并不知道的知识点。
3、有始有终
第一次学习时,学习完脚本录制之后,就停止学习了,并没有继续学习后续的内容。
第二次学习后发现,用录制的方式写脚本是很low的,很有局限性,并不能满足所有的需求,后来用WebDriver和UnitTest才是真正的高级,解决脚本录制不能解决的问题。
4、应用到日常的工作中
我们学习完自动化之后,不要学习完就行了,而要积极的将其应用到我们日常的工作中,如果放着不用,一段时间之后我们学习到的知识都会慢慢遗忘。将其应用到工作中后,不仅能对技术进行不断练习、优化、升级,还能提高工作效率,何乐而不为呢?
这是我自学自动化的历程,走了不少弯路,也没有专人的指导,只能靠自己去摸索,希望我自己犯的错误能让大家引以为戒。
5、全面了解,选好切入点
目前自动化测试方向大概有以下几个:
辅助测试脚本方向:以Shell,Python为主来简化重复的工作,过滤日志等;
接口自动化测试方向:Python+Unittest+HtmlTestRuner+Jenkins和Java+Httpclient+TestNG+Jenkins,当然还有很多其他二次开发的框架或工具,不过核心是一样的;
页面自动化方向,主要有Python+Webdrver+HtmlTestRunner+Jenkins,Java+Webdriver+TestNG+Jenkins,以及其他的框架和工具;
App自动化测试方向:以Robotium+Java+TestNG+Jenkins,
Appium+Java+TestNG+Jenkins,Appium+Python+HtmlTestRunner为主。
当然这里介绍的都是简单的,最基本的实现方案,作为入门学习比较合适。其他五花八门的二次开发的框架,包含众多功能的方案留待你以后提升。先从这几方面了解入手,选择一个语言体系,建议从接口自动化入后,然后再去学习页面和app。
一、计算机基础系列

二、Python专题

三、Python自动化测试框架应用

四、接口自动化测试

五、web、ui自动化测试
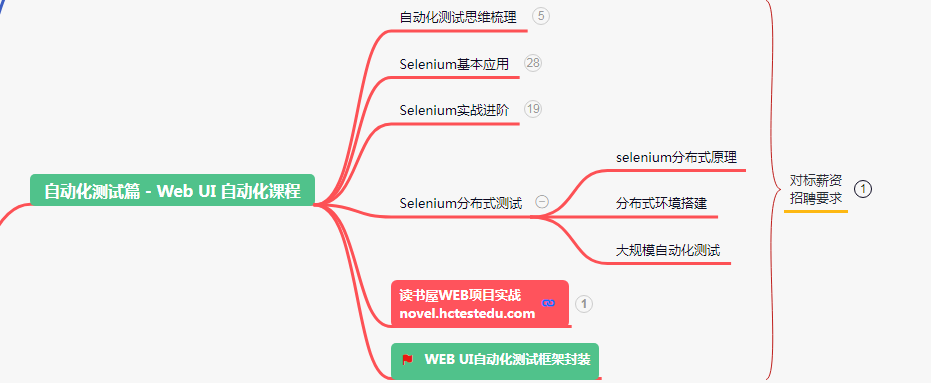
六、移动端自动化测试
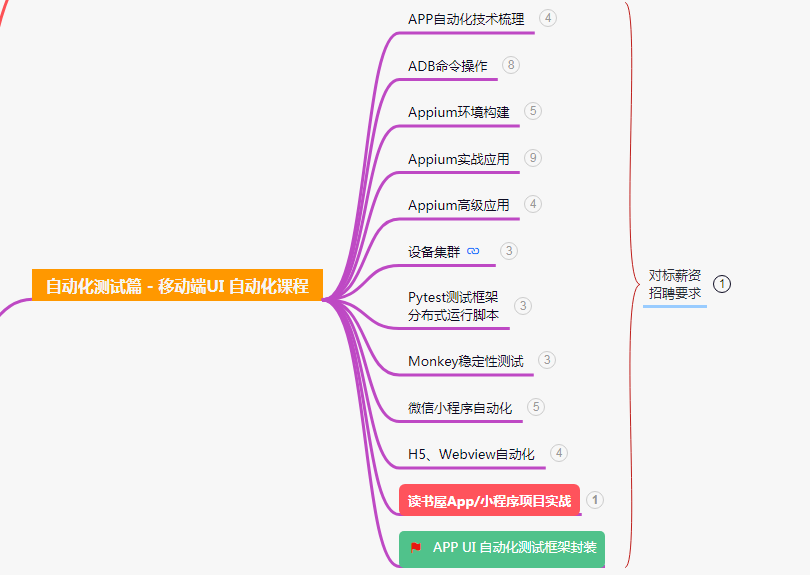
七、持续集成

八、性能测试

九、安全测试

十、跨平台自动化
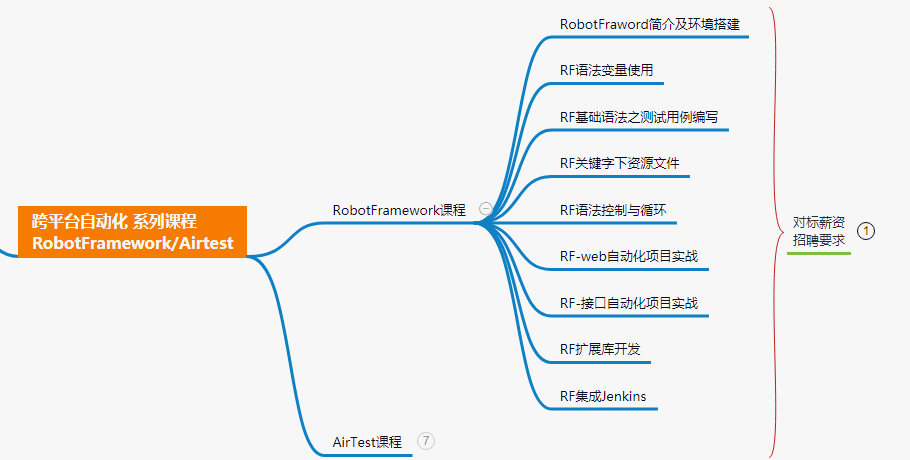
十一、测试开发
根据这个学习架构路线,不断地去摸索与提升,突破技术的瓶颈,可以说,这个过程会让你痛不欲生,但只要你熬过去了。以后的生活就轻松很多。我也是走过这样一段路,才能获得更多高薪职位的机会,付出终有回报,也算是对我能力的一种认可吧,真正的证明了自己的价值。至少税后30+的薪水是我当前状态下比较满意的。
今天的分享就到此结束了, 如果文章对你有帮助,记得点赞,收藏,加关注。会不定期分享一些干货哦......
最后感谢每一个认真阅读我文章的人,看着粉丝一路的上涨和关注,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
这些资料,对于从事【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴我走过了最艰难的路程,希望也能帮助到你!凡事要趁早,特别是技术行业,一定要提升技术功底。希望对大家有所帮助……如果你不想再体验一次自学时找不到资料,没人解答问题,坚持几天便放弃的感受的话,可以加入下方我们的测试交流群大家一起讨论交流学习。