网站设置银联密码软件发布流程
DevExpress Reporting是.NET Framework下功能完善的报表平台,它附带了易于使用的Visual Studio报表设计器和丰富的报表控件集,包括数据透视表、图表,因此您可以构建无与伦比、信息清晰的报表。
DevExpress Reports — 跨平台报表组件,允许用户在针对任何基于.NET平台的应用程序中生成报表文档,可部署在任何支持的操作系统上。在过去的几个月里,官方技术团队一直专注于增强多个环境中的报表生成进程,同时保持与主机操作系统本身的独立性。在我们深入研究细节之前,先简单介绍一下Visual Studio Code,以及为什么选择它而不是其他可用的替代品。
获取DevExpress Reporting v23.1正式版下载(Q技术交流:909157416)
在上文中(点击这里回顾>>),我们为大家介绍了DevExpress Visual Studio Code报表设计器扩展、基于VS Code扩展的技术以及一些前期配置等。本文将继续介绍如何创建一个新的DevExpress报表,欢迎持续关注我们哦~
创建一个新的DevExpress报表
此时我们准备向示例项目中添加一个新报表,扩展增加一个新的DX Reporting: New Report命令到Visual Studio代码中,只需再次按F1来使用该命令并指定新的报表名称。

VS Code将自动打开新创建的报表,并以空白报表呈现DevExpress报表设计器:
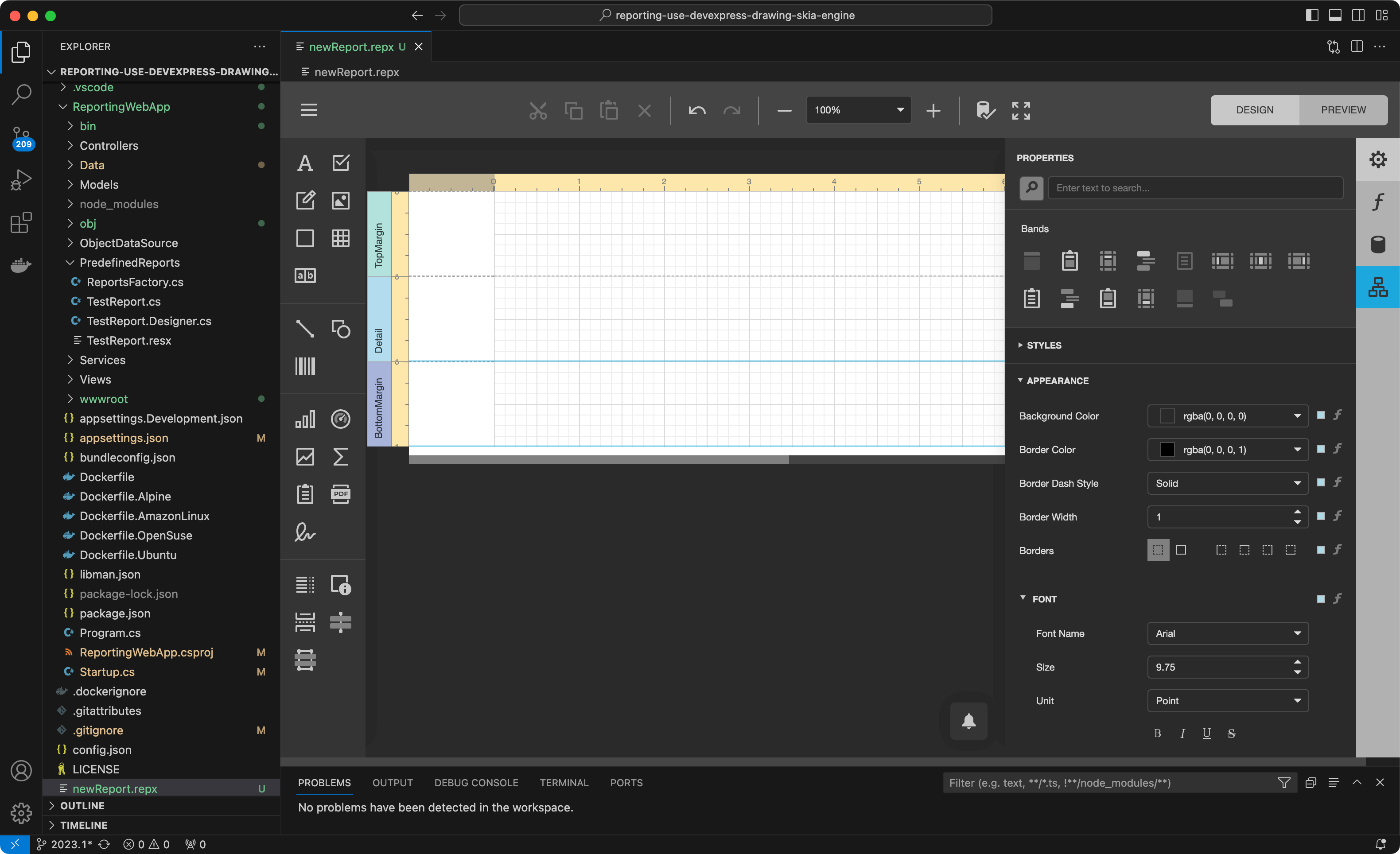
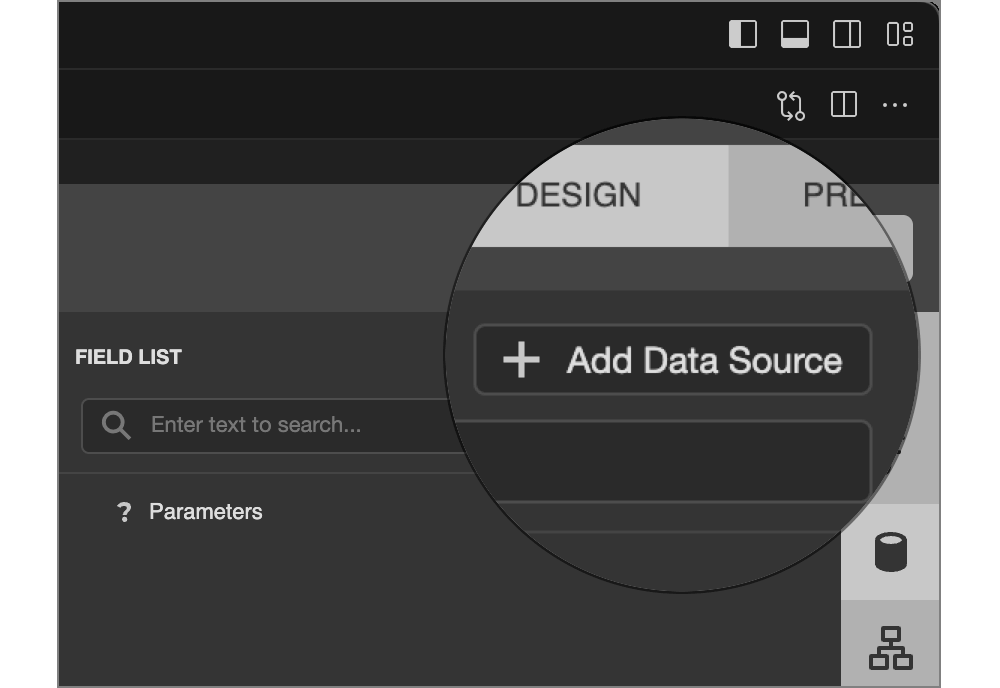
在此阶段,我们可以向该报表添加数据源,并使用内置的报表向导对其进行设计。我们将选择右侧的数据源选项卡,然后点击"Add Data Source"按钮调用数据源向导:
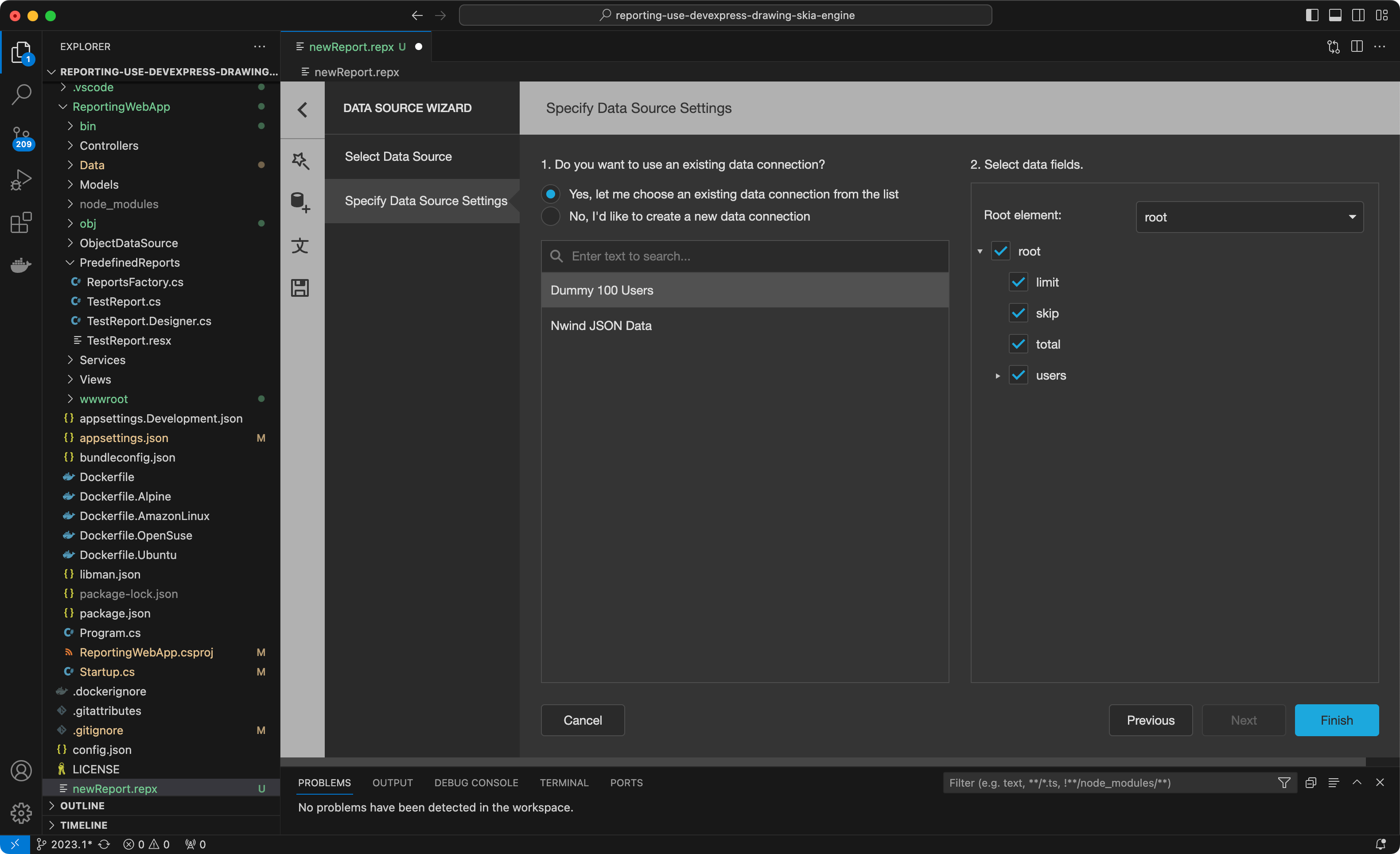
出于本示例的目的,我们将使用之前在reporting.config.file中设置的示例 "Dummy 100 Users"JSON数据源,选择可用的数据源,点击“Finish”完成操作:
接下来,我们将导航到报表设计器主菜单,并在报表向导中选择Design in Report Wizard...来启动报表向导:
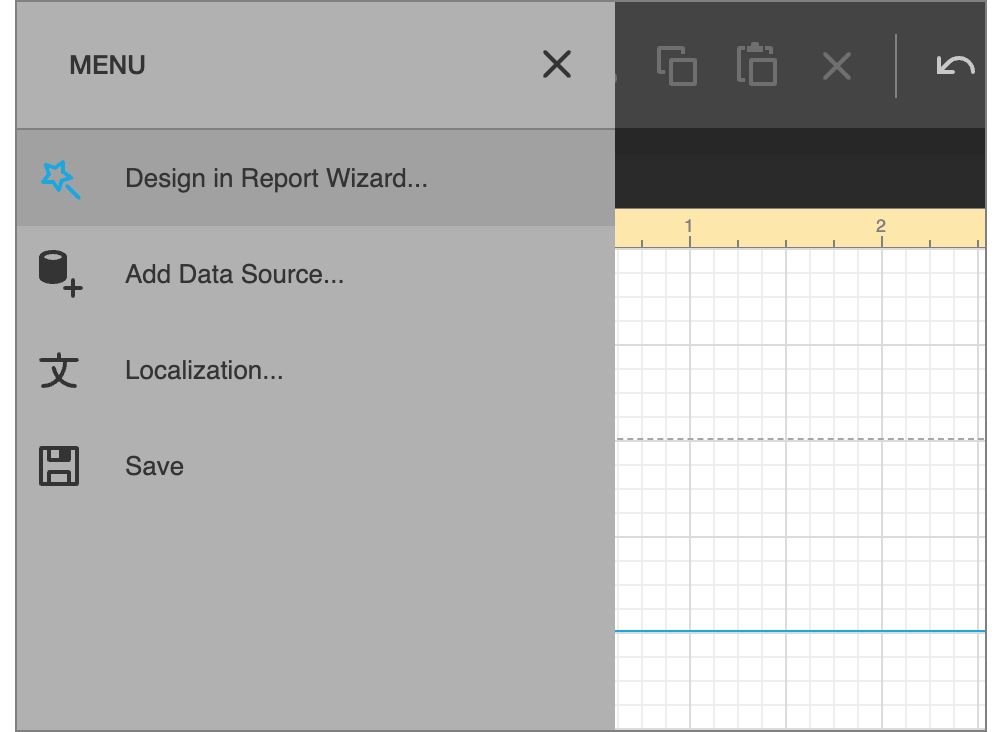
我们将按照向导提示完成报表生成过程,如果您遵循这篇文章,请确保使用“Save”快捷键保存报表模板文件(在macOS中是Command+ S)。当您这样做时,可以在屏幕上看到以下内容:
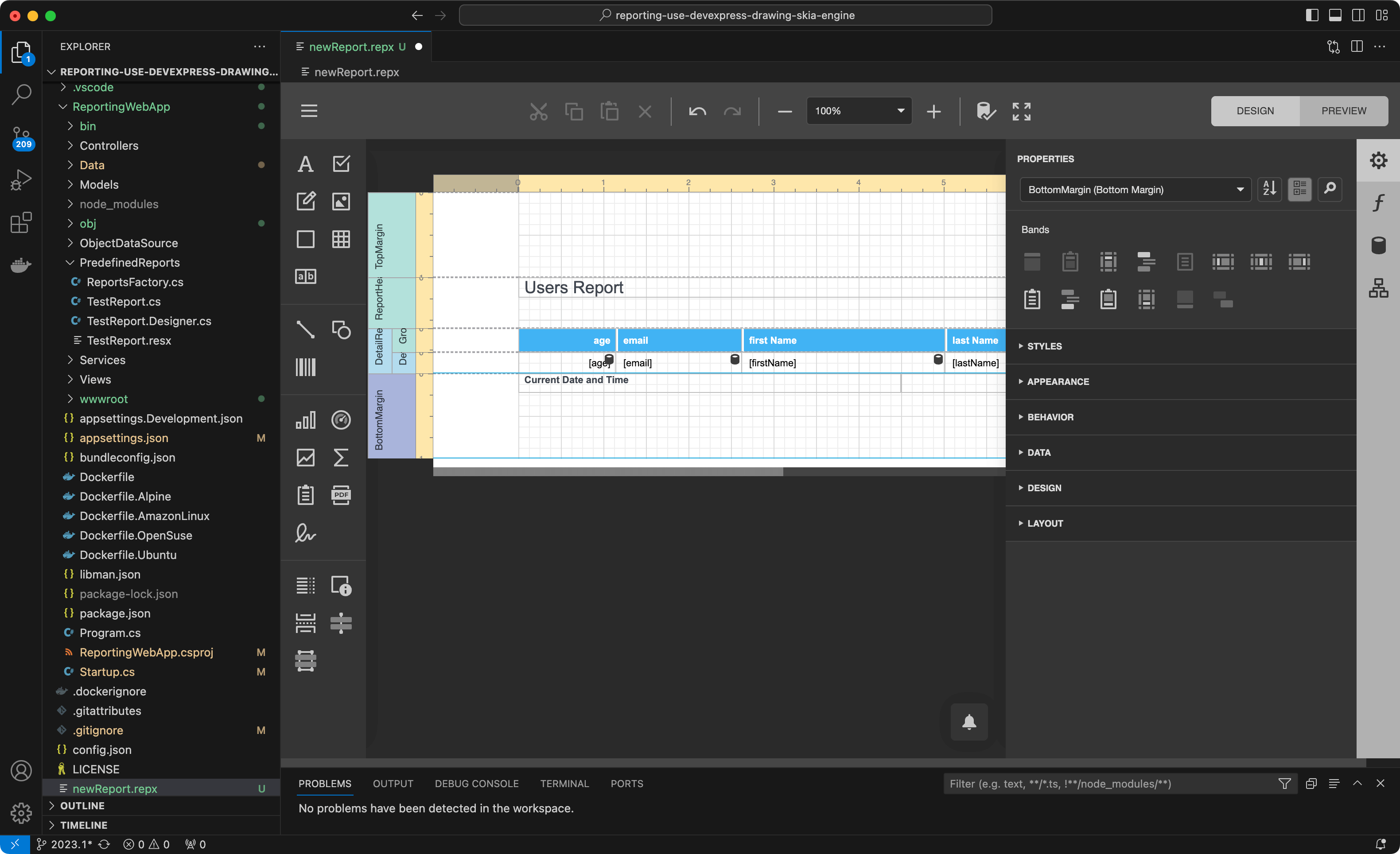
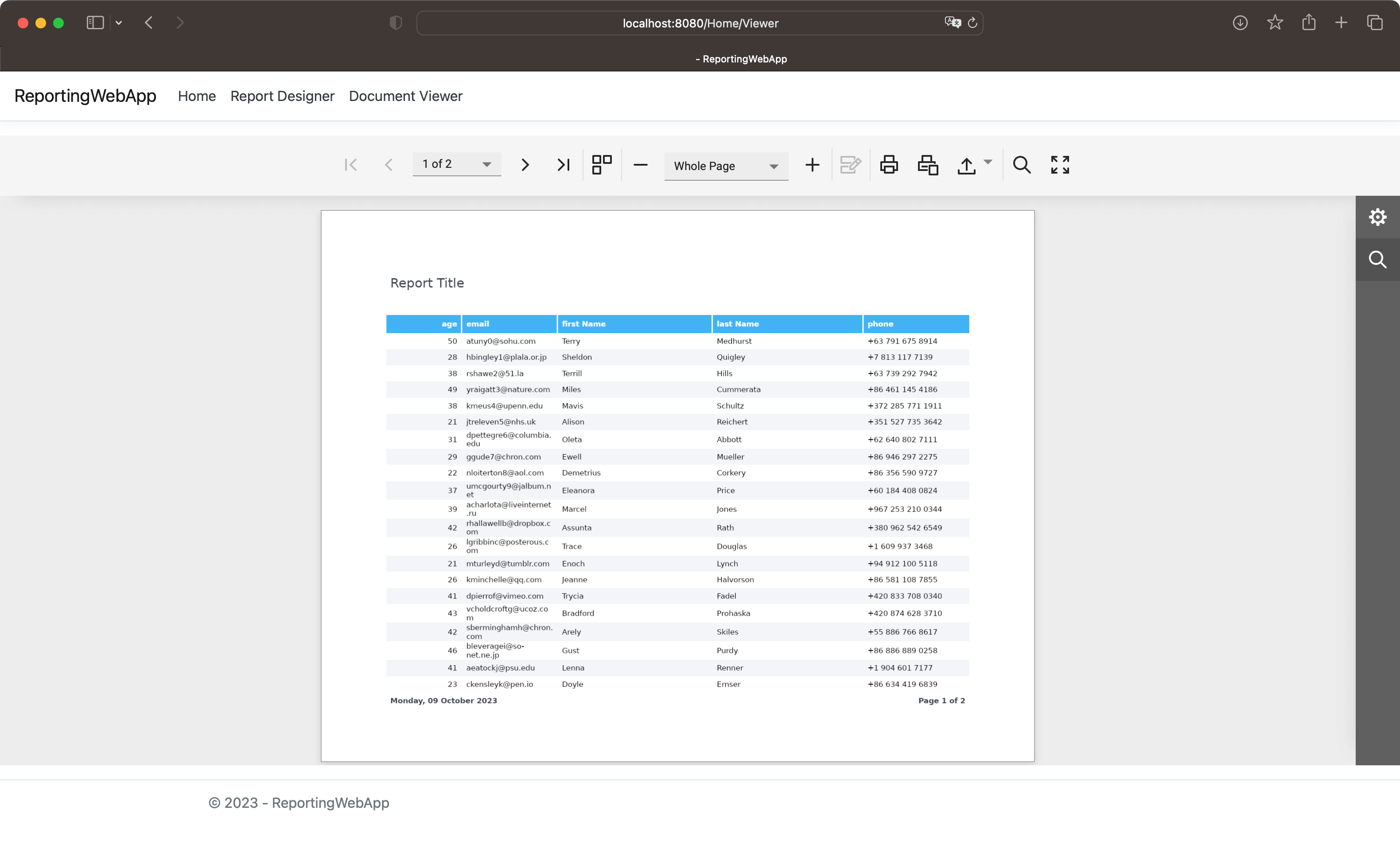
要查看结果,只需要按下"Preview" 按钮,您可以从内置的打印预览窗口打印和导出报表文档:
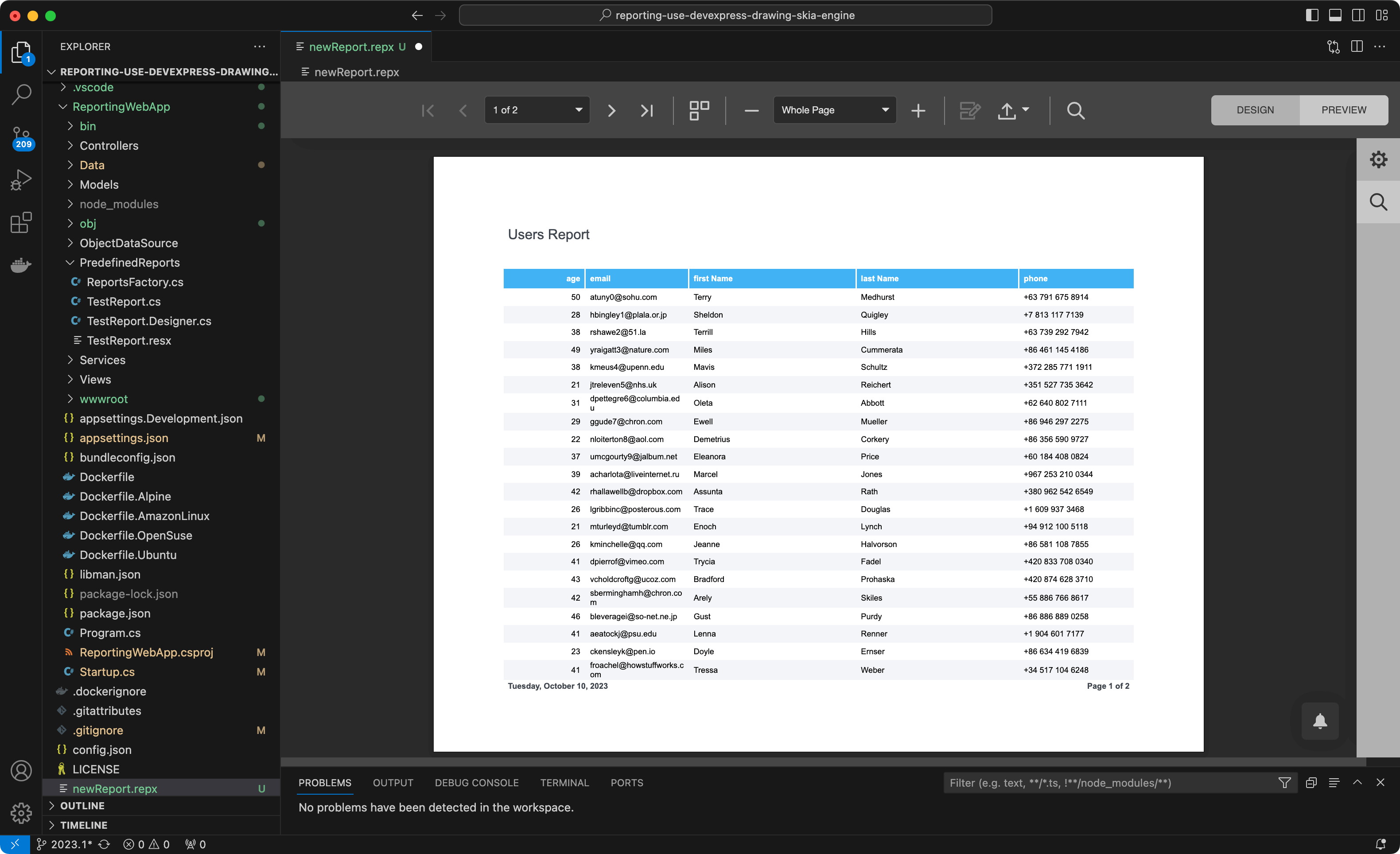
运行示例应用程序
在这个阶段,我们必须修改一些项目代码文件,以便在运行时将这个报表布局加载到XtraReport类中。首先我们必须移动 "newReport. repx" 文件到PredefinedReports目录中,完成后我们需要进行以下更改:
HomeController.cs -> Viewer method
将在文档查看器中打开的报表名称更改为newReport:
public IActionResult Viewer([FromServices] IWebDocumentViewerClientSideModelGenerator clientSideModelGenerator,
[FromQuery] string reportName) {var reportToOpen = string.IsNullOrEmpty(reportName) ? "newReport" : reportName;
var model = new Models.ViewerModel {
ViewerModelToBind = clientSideModelGenerator.GetModel(reportToOpen, WebDocumentViewerController.DefaultUri)
};
return View(model);
}ReportsFactory.cs
替换如下代码,从PredefinedReports目录加载报表模板:
public static class ReportsFactory
{
public static string ReportsPath { get; set; }
public static Dictionary<string, Func<XtraReport>> Reports = new Dictionary<string, Func<XtraReport>>()
{
["TestReport"] = () => new TestReport(),
["newReport"] = () => XtraReport.FromFile(Path.Combine(ReportsPath + "/PredefinedReports/newReport.repx"))
};}Startup.cs
修改类构造函数来将IWebEnvironment.ContnetRootPath变量传递到ReportsFactory类:
public Startup(IConfiguration configuration, IWebHostEnvironment environment) {
Configuration = configuration;
ReportsFactory.ReportsPath = environment.ContentRootPath;
AppDomain.CurrentDomain.SetData("DataDirectory", environment.ContentRootPath);
}ReportDbContext.cs -> InitializeDatabase method
将JSON数据源添加到应用程序注册的数据源集合中:
...
var Dummy100UsersConnectionName = "Dummy 100 Users";
if(!JsonDataConnections.Any(x => x.Name == Dummy100UsersConnectionName)) {
var newData = new JsonDataConnectionDescription {
Name = Dummy100UsersConnectionName,
DisplayName = "Dummy 100 Users",
ConnectionString = "Uri=https://dummyjson.com/users/"
};
JsonDataConnections.Add(newData);
}
...最后,我们需要确保在每次构建应用程序时将报表模板文件复制到应用程序输出目录中。要实现这一点,我们需要再"*. csproj"文件中添加以下内容:
<ItemGroup>
<None Remove="PredefinedReports\*.repx" />
</ItemGroup>
<ItemGroup>
<Content Include="PredefinedReports\newReport.repx">
<CopyToOutputDirectory>PreserveNewest</CopyToOutputDirectory>
</Content>
</ItemGroup>通过这些修改,我们可以切换到VS Code中的终端窗口并运行Docker容器:
export DX_NUGET=https://nuget.devexpress.com/Your_API_Token/api
DOCKER_BUILDKIT=1 docker build -t reporting-app --secret id=dxnuget,env=DX_NUGET .
docker run -p 8080:80 reporting-app:latest应用程序页面可通过以下URL访问:http://localhost:8080/,点击顶部的 "Document Viewer"链接显示刚刚在Visual Studio Code中创建的报表打印预览。