网站推广的途径和要点南通专业网站排名推广
一看就懂的RxJava源码分析
- 前言
- 零、观察模式简介
- 一、RxJava使用示例一
- 二、示例一源码分析
- 0. 示例一代码分解
- 1. RxJava中的观察者是谁?
- 2. RxJava中的被观察者又是谁?
- 3. 观察者又是如何安插到被观察者中的?
- 4. 示例一RxJava源码整体关系类图
- 4. RxJava的Hook机制
- 三、RxJava使用示例二
- 四、示例二源码分析
- 1. 同样从subscribe方法看起,看看观察者如何被安插到被观察者中
- 2. subscribe方法源码如下
- 3. subscribeActual方法是被map方法返回的对象实现,我们来看看map方法的源码
- 4. 因此接着第2步去ObservableMap类中查看subscribeActual方法的源码
- 5. 第4步提到的ObservableMap类中的source和function是什么?我们看下源码
- 6. 第5步提到的map方法属于哪个对象呢?
- 7. 我们接着第4步继续分析
- 8. 我们看看ObservableEmitter发送的数据如何被map处理,然后又被观察者接收
- 五、后记
前言
RxJava是一种基于观察者模式的异步编程库,且支持响应式编程,适用于处理复杂的事件流。RxJava是观察者模式的扩展应用,其的核心概念是Observable和Observer。Observable表示一个异步事件流,Observer表示对这个事件流的观察者。当Observable发出一个事件时,Observer会收到这个事件并进行相应的处理。RxJava还提供了一些操作符,可以对事件流进行过滤、转换、组合等操作,从而更方便地处理事件流。
本文对于RxJava的源码进行分析,以更加彻底的了解RxJava的实现思路。
零、观察模式简介
前言中我们提到RxJava是观察者模式的扩展应用,那么学习RxJava的源码,肯定要懂观察者模式的,如果不懂这种设计模式,直接来看源码是比较吃力的。本文也是以观察者模式为切入点来讲解RxJava源码。
大家可以看下我之前写的全网最全面最精华的设计模式讲解,从程序员转变为工程师的第一步,这篇文章中对于观察者模式的介绍。再啰嗦一句,设计模式非常重要,也非常难以掌握,因为它不是简单的技术,而是一种思想,这世界上最难学习的就是思想,希望各位博友能够真正将这种思想融入自己的思维中。
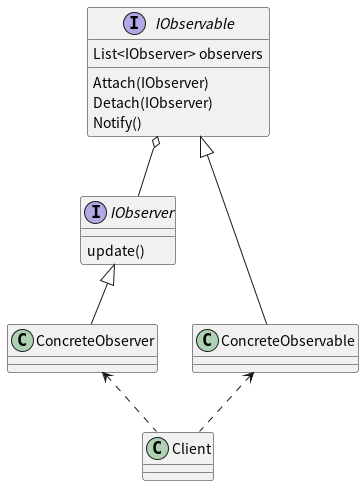
简单来说,观察者模式有两个主要角色,一个是观察者,一个是被观察者,而实现观察者模式的核心是将观察者安插(聚合)到被观察者之中,这样被观察者的一举一动都能被观察者所捕捉,而这也是分析RxJava源码的核心,如果不能理解该核心,请移步我上面提到的文章,里面有比较详细的介绍。
一、RxJava使用示例一
使用RxJava需要在build.gradle中引用RxJava库
implementation 'io.reactivex.rxjava3:rxjava:3.0.4'
implementation 'io.reactivex.rxjava3:rxandroid:3.0.0'
最简单的RxJava使用示例
public class MainActivity extends AppCompatActivity {private final static String TAG = MainActivity.class.getSimpleName();@Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);setContentView(R.layout.activity_main);Observable.create(new ObservableOnSubscribe<String>() {@Overridepublic void subscribe(@NonNull ObservableEmitter<String> emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}).subscribe(new Observer<String>() {@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull String s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}});}
}
运行结果
2023-11-17 04:12:57.125 15872-15872/com.xiaomi.myaxjava D/MainActivity: onSubscribe
2023-11-17 04:12:57.125 15872-15872/com.xiaomi.myaxjava D/MainActivity: onNext -》 sun
2023-11-17 04:12:57.126 15872-15872/com.xiaomi.myaxjava D/MainActivity: onNext -》 hao
二、示例一源码分析
示例一的代码用于实现观察者监控被观察者发送的字符串,并进行打印。
0. 示例一代码分解
- 为了便于我们更好的分析源码,我们将上面示例一中的匿名类实现全部去掉。匿名类是简化了代码,但有时候也提高了代码阅读的难度。去掉匿名类后的代码如下,看上去是不是容易理解多了。
public class MainActivity extends AppCompatActivity {private final static String TAG = MainActivity.class.getSimpleName();@Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);setContentView(R.layout.activity_main);MySource mySource = new MySource();MyObserver myObserver = new MyObserver();Observable.create(mySource).subscribe(myObserver);}private class MySource implements ObservableOnSubscribe<String>{@Overridepublic void subscribe(@NonNull ObservableEmitter emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}private class MyObserver implements Observer<String>{@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull String s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}}
}
- RxJava核心代码就一行:
Observable.create(mySource).subscribe(myObserver); - 上面我们提到RxJava是观察者模式的扩展应用,而观察者模式的核心是将观察者Observer安插到被观察者Observable之中,监视被观察者的一举一动。下面我们需要找出观察者是谁,被观察者是谁,观察者又如何被插入到被观察者之中即可。
1. RxJava中的观察者是谁?
RxJava通过subscribe方法订阅观察者(subscribe方法其实就是实现将观察者安插到被观察者,后面我们会详细介绍如何实现安插的),即示例一代码分解后中的观察者是myObserver。
private class MyObserver implements Observer<String>{@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull String s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}}
2. RxJava中的被观察者又是谁?
其实如果理解观察者设计模式的话,我们从MyObservable的具体代码中,我们也能猜到,真正的被观察者应该是ObservableEmitter对象,因为被观察者是发数据方,观察者监察被观察者发送的数据,而负责发送数据的是ObservableEmitter对象的onNext方法,因此被观察者应该是ObservableEmitter对象,后面我们会从源码中证实这一点。
private class MySource implements ObservableOnSubscribe<String>{@Overridepublic void subscribe(@NonNull ObservableEmitter emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}
3. 观察者又是如何安插到被观察者中的?
上面我们提到RxJava通过subscribe方法订阅观察者,即通过subscribe方法将观察者安插到被观察者中。下面我们开始分析subscribe方法的源码,看看观察者(示例中的myObserver)如何被安插到被观察者中。
- 示例一的RxJava核心代码就是下面一句
Observable.create(mySource).subscribe(myObserver);
- subscribe方法是属于哪个对象呢?
很明显,subscribe方法的对象是由Observable.create()方法创建的,下面我们看看Observable.create方法的源码:
public static <T> Observable<T> create(@NonNull ObservableOnSubscribe<T> source) {Objects.requireNonNull(source, "source is null");return RxJavaPlugins.onAssembly(new ObservableCreate<>(source));}
create方法传入了我们自定义的MySource对象,返回时又被RxJavaPlugins.onAssembly方法处理了一下,我们来看看RxJavaPlugins.onAssembly方法:
public static <T> Observable<T> onAssembly(@NonNull Observable<T> source) {Function<? super Observable, ? extends Observable> f = onObservableAssembly;if (f != null) {return apply(f, source);}return source;}
可以看到如果onObservableAssembly为null,那么onAssembly方法就什么都不做,如果不为null就对source进行处理一下再返回,其实这就是RxJava的Hook机制,也就是通过onAssembly方法拦截一下被观察者,先对被观察者处理一波,后面我们会详细介绍,这儿我们忽略这个hook即可。
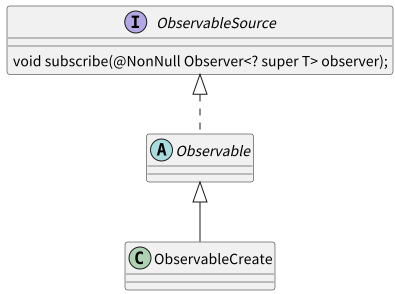
那么Observable.create()方法创建的就是ObservableCreate对象,即该案例中subscribe方法是ObservableCreate对象的方法。ObservableCreate的类图如下,subscribe方法被抽象类Observable所实现。
3. subscribe方法的源码如下
public final void subscribe(@NonNull Observer<? super T> observer) {Objects.requireNonNull(observer, "observer is null");try {observer = RxJavaPlugins.onSubscribe(this, observer);Objects.requireNonNull(observer, "The RxJavaPlugins.onSubscribe hook returned a null Observer. Please change the handler provided to RxJavaPlugins.setOnObservableSubscribe for invalid null returns. Further reading: https://github.com/ReactiveX/RxJava/wiki/Plugins");subscribeActual(observer); //这个是核心方法} catch (NullPointerException e) { // NOPMDthrow e;} catch (Throwable e) {Exceptions.throwIfFatal(e);// can't call onError because no way to know if a Disposable has been set or not// can't call onSubscribe because the call might have set a Subscription alreadyRxJavaPlugins.onError(e);NullPointerException npe = new NullPointerException("Actually not, but can't throw other exceptions due to RS");npe.initCause(e);throw npe;}}
看源码我们要先梳理主线,一定不要想着一开始每一句都看懂(因为这样大概率会看晕),一些支线的细节代码可以先不关注,重点是关注主线代码。
大概一看subscribe方法中核心方法是subscribeActual(observer)方法,上面我们分析了subscribe方法属于ObservableCreate对象,那么subscribeActual方法自然也是属于ObservableCreate类,我们去ObservableCreate类中查看subscribeActual方法的源码如下:
@Overrideprotected void subscribeActual(Observer<? super T> observer) {CreateEmitter<T> parent = new CreateEmitter<>(observer);//这里创建了CreateEmitter对象,并将我们的观察者传进去了observer.onSubscribe(parent);//观察者执行onSubscribe方法。这里就能明白为什么观察者都是先执行onSubscribe方法了try {source.subscribe(parent);//这里的source是谁呢?} catch (Throwable ex) {Exceptions.throwIfFatal(ex);parent.onError(ex);}}
subscribeActual方法中首先创建了CreateEmitter对象,并将我们自定义的观察者聚合进去。其实,从这就证实了,CreateEmitter对象是被观察者,CreateEmitter通过构造函数将观察者注入,如此以来,观察者就被安插进了被观察者之中,具体如何监控被观察者,我们后面再说。
其次,subscribeActual方法不管三七二十一先执行观察者的onSubscribe方法,这里也能说明为什么RxJava都是先执行onSubscribe方法。
最后,subscribeActual方法执行source.subscribe(parent),将创建的被观察者即CreateEmitter对象parent传递了出去,那么这里的source又是谁呢?我们看看源码中source赋值的地方
public final class ObservableCreate<T> extends Observable<T> {final ObservableOnSubscribe<T> source;public ObservableCreate(ObservableOnSubscribe<T> source) {this.source = source;//通过ObservableCreate构造函数传入source的值}@Overrideprotected void subscribeActual(Observer<? super T> observer) {CreateEmitter<T> parent = new CreateEmitter<>(observer);observer.onSubscribe(parent);try {source.subscribe(parent);} catch (Throwable ex) {Exceptions.throwIfFatal(ex);parent.onError(ex);}}
}
从源码中可以看到source是创建ObservableCreate对象的时候传入的,上面分析subscribe方法是属于哪个对象的时候,我们就看到ObservableCreate对象是由Observable.create创建的
Observable.create(mySource).subscribe(myObserver);public static <T> Observable<T> create(@NonNull ObservableOnSubscribe<T> source) {Objects.requireNonNull(source, "source is null");return RxJavaPlugins.onAssembly(new ObservableCreate<>(source));//这里的source就是我们自定的mySource}private class MySource implements ObservableOnSubscribe<String>{@Overridepublic void subscribe(@NonNull ObservableEmitter emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}
这时我们再看subscribeActual方法源码
@Overrideprotected void subscribeActual(Observer<? super T> observer) {CreateEmitter<T> parent = new CreateEmitter<>(observer);observer.onSubscribe(parent);try {source.subscribe(parent);//source就是我们自定义MySource对象} catch (Throwable ex) {Exceptions.throwIfFatal(ex);parent.onError(ex);}}
source.subscribe(parent)中的source就是我们自定义的MySource对象,通过subscribe方法将subscribeActual方法中创建的被观察者CreateEmitter对象parent传递到MySource中。此时,我们再看被观察者发送数据时,观察者是如何监察到的
private class MySource implements ObservableOnSubscribe<String>{@Overridepublic void subscribe(@NonNull ObservableEmitter emitter) throws Throwable {emitter.onNext("sun");//emitter就是subscribeActual方法中创建的CreateEmitter对象emitter.onNext("hao");}}
被观察者emitter通过onNext发送数据,我们来看看onNext方法的源码
static final class CreateEmitter<T>extends AtomicReference<Disposable>implements ObservableEmitter<T>, Disposable {private static final long serialVersionUID = -3434801548987643227L;final Observer<? super T> observer;CreateEmitter(Observer<? super T> observer) {this.observer = observer;}@Overridepublic void onNext(T t) {if (t == null) {onError(ExceptionHelper.createNullPointerException("onNext called with a null value."));return;}if (!isDisposed()) {observer.onNext(t);//观察者接收到被观察者发送的数据}}}
可以看到当被观察者对象调用onNext方法时,安插在内部的观察者会接收到数据,而观察者的onNext方法就是我们自定义实现的
private class MyObserver implements Observer<String>{@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull String s) {Log.d(TAG, "onNext -》 "+s);//监察到被观察者发送的数据}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}}
4. 示例一RxJava源码整体关系类图
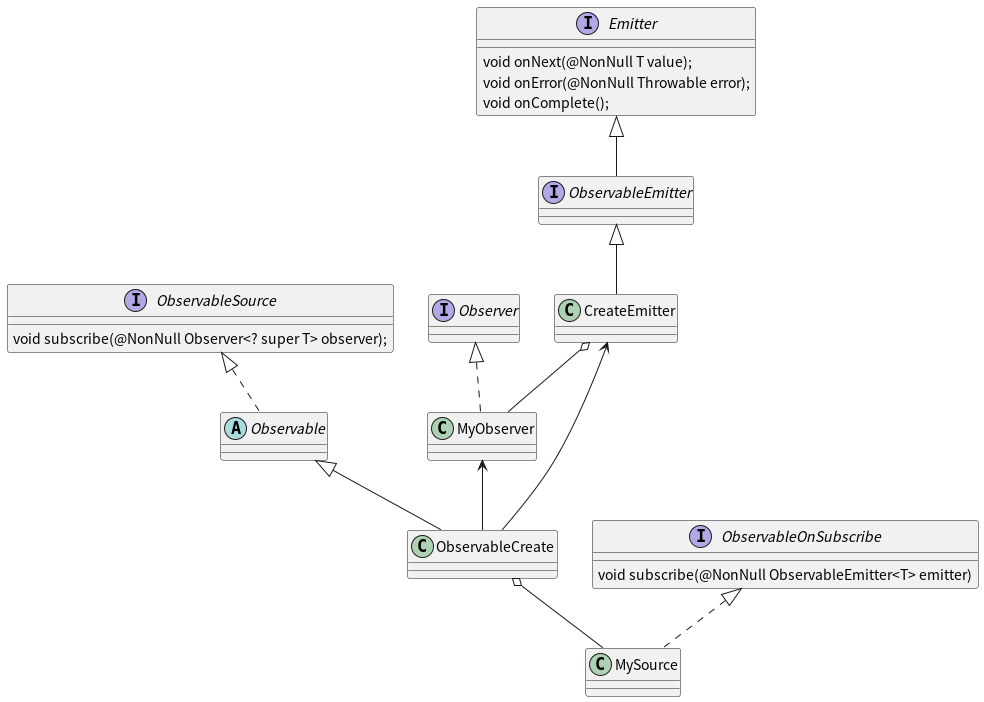
ObservableCreate就是一个中转器,它把MySource和MyObserver中转出去,之后观察者MyObserver聚合(安插)到被观察者CreateEmitter对象,最后,被观察者对象又通过subscribe方法被传递给MySource对象。
4. RxJava的Hook机制
- 上面我们也提到了该机制,Observable的create方法源码如下
public static <T> Observable<T> create(@NonNull ObservableOnSubscribe<T> source) {Objects.requireNonNull(source, "source is null");return RxJavaPlugins.onAssembly(new ObservableCreate<>(source));}
创建ObservableCreate对象之后,又被RxJavaPlugins.onAssembly方法处理一下才返回,这个就是RxJava的hook机制,其实就是将创建的被观察者先自己玩一把,再给观察者处理。
- RxJavaPlugins.onAssembly方法源码如下:
static volatile Function<? super Observable, ? extends Observable> onObservableAssembly;public static <T> Observable<T> onAssembly(@NonNull Observable<T> source) {Function<? super Observable, ? extends Observable> f = onObservableAssembly;if (f != null) {//如果设置了onObservableAssembly,则意味着开启hookreturn apply(f, source);}return source;}static <T, R> R apply(@NonNull Function<T, R> f, @NonNull T t) {try {return f.apply(t);} catch (Throwable ex) {throw ExceptionHelper.wrapOrThrow(ex);}}
通过如下方法给onObservableAssembly赋值
public static void setOnObservableAssembly(@Nullable Function<? super Observable, ? extends Observable> onObservableAssembly) {if (lockdown) {throw new IllegalStateException("Plugins can't be changed anymore");}RxJavaPlugins.onObservableAssembly = onObservableAssembly;}
使用RxJava的hook机制示例
RxJavaPlugins.setOnObservableAssembly(new Function<Observable, Observable>() {@Overridepublic Observable apply(Observable observable) throws Throwable {return null;//在这拦截住Observable,自己先处理一波}});
三、RxJava使用示例二
public class MainActivity extends AppCompatActivity {private final static String TAG = MainActivity.class.getSimpleName();@Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);setContentView(R.layout.activity_main);Observable.create(new ObservableOnSubscribe<String>() {@Overridepublic void subscribe(@NonNull ObservableEmitter<String> emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}).map(new Function<String, Integer>() {@Overridepublic Integer apply(String s) throws Throwable {Integer ans = 0;if (s.equals("sun")){ans = 66;}else if (s.equals("hao")){ans = 99;}else{ans = 88;}return ans;}}).subscribe(new Observer<Integer>() {@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull Integer s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}});}
}
运行结果如下:
2023-11-17 04:58:08.660 16545-16545/com.xiaomi.myaxjava D/MainActivity: onSubscribe
2023-11-17 04:58:08.660 16545-16545/com.xiaomi.myaxjava D/MainActivity: onNext -》 66
2023-11-17 04:58:08.660 16545-16545/com.xiaomi.myaxjava D/MainActivity: onNext -》 99
四、示例二源码分析
示例二比示例一稍微复杂一点,加了map操作符,map操作符的作用是将被观察者发送的数据先做一波处理再给观察者。有了示例一源码的基础,分析示例二源码也比较简单了。在分析该部分源码前建议先去看一下我之前写的装饰模式,RxJava就是通过装饰模式将一个个的操作符装饰为各种类型的观察者(都是Observer的子类)。
1. 同样从subscribe方法看起,看看观察者如何被安插到被观察者中
Observable.create(new ObservableOnSubscribe<String>() {@Overridepublic void subscribe(@NonNull ObservableEmitter<String> emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}).map(new Function<String, Integer>() {@Overridepublic Integer apply(String s) throws Throwable {Integer ans = 0;if (s.equals("sun")){ans = 66;}else if (s.equals("hao")){ans = 99;}else{ans = 88;}return ans;}}).subscribe(new Observer<Integer>() {//subscribe方法是哪个对象的方法?很明显是map方法返回的对象@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull Integer s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}});
2. subscribe方法源码如下
public final void subscribe(@NonNull Observer<? super T> observer) {Objects.requireNonNull(observer, "observer is null");try {observer = RxJavaPlugins.onSubscribe(this, observer);Objects.requireNonNull(observer, "The RxJavaPlugins.onSubscribe hook returned a null Observer. Please change the handler provided to RxJavaPlugins.setOnObservableSubscribe for invalid null returns. Further reading: https://github.com/ReactiveX/RxJava/wiki/Plugins");subscribeActual(observer);//该方法是被哪个类实现的?很明显subscribe方法别哪个类实现,该方法就是被哪个方法实现} catch (NullPointerException e) { // NOPMDthrow e;} catch (Throwable e) {Exceptions.throwIfFatal(e);// can't call onError because no way to know if a Disposable has been set or not// can't call onSubscribe because the call might have set a Subscription alreadyRxJavaPlugins.onError(e);NullPointerException npe = new NullPointerException("Actually not, but can't throw other exceptions due to RS");npe.initCause(e);throw npe;}}
3. subscribeActual方法是被map方法返回的对象实现,我们来看看map方法的源码
public final <R> Observable<R> map(@NonNull Function<? super T, ? extends R> mapper) {Objects.requireNonNull(mapper, "mapper is null");//示例一中讲解过RxJavaPlugins.onAssembly是hook函数,在此我们不考虑,那么返回的就是ObservableMap对象return RxJavaPlugins.onAssembly(new ObservableMap<>(this, mapper));}
4. 因此接着第2步去ObservableMap类中查看subscribeActual方法的源码
@Overridepublic void subscribeActual(Observer<? super U> t) {source.subscribe(new MapObserver<T, U>(t, function));//这里面的source和function是什么?我们后面分析}
可以看到subscribeActual方法中将我们自定义的观察者送入了MapObserver的构造函数,这儿就是采用装饰模型将我们自定义的观察者进行装饰,形成一个新的观察者。我们看下MapObserver的源码
static final class MapObserver<T, U> extends BasicFuseableObserver<T, U> {final Function<? super T, ? extends U> mapper;MapObserver(Observer<? super U> actual, Function<? super T, ? extends U> mapper) {super(actual); //把我们自定义的观察者传递给了MapObserver的父类this.mapper = mapper;}@Overridepublic void onNext(T t) {...}}
}
我们接着看MapObserver的父类BasicFuseableObserver是如何处理我们自定义的观察者的
public abstract class BasicFuseableObserver<T, R> implements Observer<T>, QueueDisposable<R> {/** The downstream subscriber. */protected final Observer<? super R> downstream;/*** Construct a BasicFuseableObserver by wrapping the given subscriber.* @param downstream the subscriber, not null (not verified)*/public BasicFuseableObserver(Observer<? super R> downstream) {this.downstream = downstream;//将我们自定义的观察者赋值给了downstream}
}
到这儿我们知道自定义的观察者最终被传递给了downstream,下面我们分析ObservableMap类中的source和function是什么?
5. 第4步提到的ObservableMap类中的source和function是什么?我们看下源码
public final class ObservableMap<T, U> extends AbstractObservableWithUpstream<T, U> {final Function<? super T, ? extends U> function;// source和function都是通过ObservableMap的构造函数传入的public ObservableMap(ObservableSource<T> source, Function<? super T, ? extends U> function) {super(source);this.function = function;}@Overridepublic void subscribeActual(Observer<? super U> t) {source.subscribe(new MapObserver<T, U>(t, function));}
}
source和function都是通过ObservableMap的构造函数传入的,第3步我们分析map源码的时候看到创建了ObservableMap对象
public final <R> Observable<R> map(@NonNull Function<? super T, ? extends R> mapper) {Objects.requireNonNull(mapper, "mapper is null");//这里的mapper就是我们自定义的Function//那这里的this是谁呢?很明显map方法属于哪个对象,这个this是那个对象return RxJavaPlugins.onAssembly(new ObservableMap<>(this, mapper));}
6. 第5步提到的map方法属于哪个对象呢?
Observable.create(new ObservableOnSubscribe<String>() {@Overridepublic void subscribe(@NonNull ObservableEmitter<String> emitter) throws Throwable {emitter.onNext("sun");emitter.onNext("hao");}}).map(new Function<String, Integer>() {//map方法是Observable.create方法返回的对象@Overridepublic Integer apply(String s) throws Throwable {Integer ans = 0;if (s.equals("sun")){ans = 66;}else if (s.equals("hao")){ans = 99;}else{ans = 88;}return ans;}}).subscribe(new Observer<Integer>() {@Overridepublic void onSubscribe(@NonNull Disposable d) {Log.d(TAG, "onSubscribe");}@Overridepublic void onNext(@NonNull Integer s) {Log.d(TAG, "onNext -》 "+s);}@Overridepublic void onError(@NonNull Throwable e) {Log.d(TAG, "onError");}@Overridepublic void onComplete() {Log.d(TAG, "onComplete");}});
我们接着看Observable.create方法的源码
public static <T> Observable<T> create(@NonNull ObservableOnSubscribe<T> source) {Objects.requireNonNull(source, "source is null");//返回的是一个ObservableCreate的对象,这里的source是我们自定义的ObservableOnSubscribe对象return RxJavaPlugins.onAssembly(new ObservableCreate<>(source));}
到这儿我们知道ObservableMap类中的function就是我们在map方法中传入的自定义Function匿名类,source就是我们通过Observable.create方法创建的ObservableCreate对象
7. 我们接着第4步继续分析
@Overridepublic void subscribeActual(Observer<? super U> t) {//source就是我们通过Observable.create方法创建的ObservableCreate对象//function就是我们在map方法中传入的自定义Function匿名类source.subscribe(new MapObserver<T, U>(t, function));}
我们再来看ObservableCreate类中实现的subscribe方法,ObservableCreate继承自Observable,ObservableCreate实现的subscribe也是继承自Observable,因此我们去Observable中查看subscribe方法的源码
public final void subscribe(@NonNull Observer<? super T> observer) {Objects.requireNonNull(observer, "observer is null");try {observer = RxJavaPlugins.onSubscribe(this, observer);Objects.requireNonNull(observer, "The RxJavaPlugins.onSubscribe hook returned a null Observer. Please change the handler provided to RxJavaPlugins.setOnObservableSubscribe for invalid null returns. Further reading: https://github.com/ReactiveX/RxJava/wiki/Plugins");subscribeActual(observer);//把装饰后的MapObserver对象通过subscribeActual方法传递出去} catch (NullPointerException e) { // NOPMDthrow e;} catch (Throwable e) {Exceptions.throwIfFatal(e);// can't call onError because no way to know if a Disposable has been set or not// can't call onSubscribe because the call might have set a Subscription alreadyRxJavaPlugins.onError(e);NullPointerException npe = new NullPointerException("Actually not, but can't throw other exceptions due to RS");npe.initCause(e);throw npe;}}
我们接着看ObservableCreate类中的subscribeActual方法源码,这个时候就和之前示例一分析的源码接上了,就不再详细分析
@Overrideprotected void subscribeActual(Observer<? super T> observer) {//创建CreateEmitter对象,并将MapObserver对象传递进去CreateEmitter<T> parent = new CreateEmitter<>(observer);observer.onSubscribe(parent);try {//这里的source就是我们传入Observable.create方法的自定义ObservableOnSubscribe匿名类//那么subscribe方法就是我们外面自己实现的方法source.subscribe(parent);} catch (Throwable ex) {Exceptions.throwIfFatal(ex);parent.onError(ex);}}
@Overridepublic void subscribe(@NonNull ObservableEmitter<String> emitter) throws Throwable {//emitter就是上面subscribeActual方法中实例化的CreateEmitter对象emitter.onNext("sun");emitter.onNext("hao");}
8. 我们看看ObservableEmitter发送的数据如何被map处理,然后又被观察者接收
ObservableEmitter通过onNext发送数据,以emitter.onNext(“sun”)为例,我们看下onNext的源码
@Overridepublic void onNext(T t) {if (t == null) {onError(ExceptionHelper.createNullPointerException("onNext called with a null value."));return;}if (!isDisposed()) {observer.onNext(t);//这里的observer就是ObservableMap对象,t是我们发送的数据“sun”}}
接着我们再看下ObservableMap中的onNext方法源码
@Overridepublic void onNext(T t) {// t = "sun"if (done) {return;}if (sourceMode != NONE) {downstream.onNext(null);return;}U v;try {//这里的mapper就是我们外面在map方法中传入的自定义Function,在此map先对发送的数据“sun”做了处理v = Objects.requireNonNull(mapper.apply(t), "The mapper function returned a null value.");} catch (Throwable ex) {fail(ex);return;}//downstream就是我们外面subscribe方法中传入的自定义Observer对象downstream.onNext(v);//这时候拿到数据是经过map处理后的数据}@Overridepublic Integer apply(String s) throws Throwable {Integer ans = 0;if (s.equals("sun")){ans = 66;}else if (s.equals("hao")){ans = 99;}else{ans = 88;}return ans;}
至此,整个示例二的源码我们就分析完了
五、后记
这也是我们第一次输出分析源码的文章,一是帮助自己理清楚RxJava源码流程,二是希望能够对其他博友有所帮忙,但第一次写源码分析类的文章,确实经验不足,感觉写的还是有点混乱,没有写出自己的预期,后面继续努力。
总之,就针对RxJava的源码,个人任务掌握一个切入点就对了,那就是从subscribe方法入手,看看我们自定义的观察者如何与发送数据的被观察者关联在一起的。
