院校网站建设网站设计与制作说明书
1 什么是迭代器,生成器,装饰器
2 django的信号用过吗?如何用,干过什么
3 什么是深拷贝,什么是浅拷贝,如何使用
3.1 浅拷贝
3.2 深拷贝
3.3 扩展(slice操作符和list构造函数)
1 什么是迭代器,生成器,装饰器
迭代:一种不依赖于索引取值的方式,我们不需要关注它的位置,只要能够一个个取值,它就称之为迭代-基于索引,下标的取值-不依赖于索引,没有位置的表示-for循环, next()可迭代对象:可以迭代的(for,next取值的)python中的对象称之为可迭代对象在python中可以被for循环或可以 变量.next() 取值的对象称之为可迭代对象有 :字典,列表,字符串,元组,集合,文件对象迭代器:可迭代对象调用__iter__,就得到了迭代器,迭代器有__iter__和__next__方法自定义迭代器:写个类,类中重写__iter__和__next__方法,这个类的对象就是迭代器生成器:生成器本质就是迭代器,迭代器不一定是生成器函数中只要有 yield 关键字,这个函数被调用 函数(),它就变成了生成器生成器表达式,也可以做出生成器 (i+1 for i in [1,2,3])比如有一堆数据,要放到列表中,但 你没放,而放到了生成器中for 循环生成器---》可以惰性取值,可以节省内存在哪里用过生成器?-读取文件,for循环文件 内部其实就是在用生成器-我猜测:django中orm 查询一个表所有内容 Book.objects.all()--->内部应该也是一个生成器-redis hascan 和 hsacn_iter-类似于这种场景我是可以用到它的:比如我要取数据,但是数据量比较大,不要一次性把把数据取到内存中,而是一点点取值,这样就可以把它做成一个生成器,可以节约内存 装饰器:本身是一个闭包函数,作用是在不改变 被装饰对象源代码和调用方式的基础上,为它加入新功能flask的路由就是基于装饰器django的信号也可以用装饰器方式注册django中局部去除csrf认证为接口记录访问日志认证,权限装饰器。。闭包函数:1 定义在函数内部 2 对外部作用域有引用多了一种给函数传参的方式典型应用就是装饰器所有语言都有闭包函数---》所有语言就可以实现装饰器--》但是没有装饰器的语法糖2 django的信号用过吗?如何用,干过什么
1 django信号是什么?django提供的一种通知机制,他是设计模式观察者模式(发布订阅),在发生某种变化的时候,通知某个函数执行-23种设计模式:https://www.cnblogs.com/liuqingzheng/p/10038958.html2 如何用---》内置信号 自定义信号1 内置信号:如果是内置信号用起来简单,只需要写个函数,跟内置信号绑定,当信号被触发,函数就会执行-绑定信号,在django中有两种方式@receiverconnect连接2 自定义信号:就比内置信号多了两步:1 定义信号 2 触发信号 信号.send3 使用场景:记录日志(book插入一条数据就记录日志)用户密码修改,发送邮件通知一旦生成订单,干xx事数据库中插入数据,把数据同步到别的位置4 补充python发邮件:参考博客:https://www.cnblogs.com/liuqingzheng/articles/10072695.html# 钉钉通知 django集成钉钉通知5 观察者模式:也叫发布-订阅模式定义:对象间一种一对多的依赖关系,使得当该对象状态改变时,所有依赖于它的对象都会得到通知,并被自动更新6 通过信号实现,只要book表插入一条记录,redis就跟着同步数据库中:id name price publish1 金瓶梅 29 北京出版社redis:[{id:1,name:金瓶梅,price:29,publish:北京出版社}]# book=Book.object.create(**request.data)# 使用信号def xx(*arg,**kwargs):if book表conn.rpush('key',json.dumps({})信号.connect(xx)3 什么是深拷贝,什么是浅拷贝,如何使用
# 无论深拷贝还是浅拷贝都是用来 复制对象的
# 如果是浅copy,只会复制一层,如果copy的对象中有可变数据类型,修改可变数据类型还会影响拷贝的对象
# 如果是深copy,完整复制,无论可变或不可变,都是创建出新的来,以后再改原对象,都不会对copy出的对象造成影响浅拷贝和深拷贝是Python中两种常用的复制对象的方法。1 浅拷贝创建一个新对象,但是这个新对象只是原始对象的一个引用;而深拷贝创建一个新对象,并且这个新对象与原始对象没有任何关联。在实际开发中,我们需要根据具体的情况选择使用哪种方法。2 如果我们需要复制的对象只包含基本数据类型,那么使用浅拷贝就足够了。但是,如果我们需要复制的对象包含嵌套的对象,那么就需要使用深拷贝。因为浅拷贝只是复制了引用,而深拷贝则会递归地复制整个对象树。除了copy()和deepcopy()方法外,Python还提供了其他一些复制对象的方法,如slice操作符、list()构造
函数等。这些方法也可以用于复制对象,但是它们都只能进行浅拷贝,不能进行深拷贝。-在使用深拷贝时,需要注意以下几点:1 深拷贝可能会比较耗时,因为它需要递归地复制整个对象树。2 深拷贝可能会导致循环引用的问题。如果被复制的对象中存在循环引用,那么深拷贝会进入死循环,直到Python的最大递归深度被达到为止。3 深拷贝可能会导致内存占用过高的问题。如果被复制的对象非常大,那么深拷贝会占用大量的内存。3.1 浅拷贝
"""
浅拷贝是指创建一个新对象,但是这个新对象只是原始对象的一个引用。
也就是说,在新对象中,原始对象中的所有元素都只是引用。
如果原始对象中的元素发生了变化,那么新对象中的元素也会发生变化。
"""# 1.1 使用方法
# 在Python中,可以使用copy()方法来进行浅拷贝。例如:
# 创建了一个包含一个整数和一个列表的列表,并使用copy()方法将其浅拷贝到了另一个变量中
list1 = [1, 2, [3, 4]]
list2 = list1.copy()
print(list2) # [1, 2, [3, 4]]# 浅拷贝的工作原理:
list1 = [1, 2, [3, 4]]
list2 = list1.copy()print("list1:", list1) # list1: [1, 2, [3, 4]]
print("list2:", list2) # list2: [1, 2, [3, 4]]list1[2][0] = 5 # 修改原始列表中的嵌套列表时,新列表中的相应元素也被修改了print("list1:", list1) # list1: [1, 2, [5, 4]
print("list2:", list2) # list2: [1, 2, [5, 4]]3.2 深拷贝
"""
深拷贝是指创建一个新对象,并且这个新对象与原始对象没有任何关联。
也就是说,在新对象中,原始对象中的所有元素都被复制到了新的内存地址中。
如果原始对象中的元素发生了变化,那么新对象中的元素不会受到影响。
"""
# 使用方法
# 在Python中,可以使用deepcopy()方法来进行深拷贝。例如:
# 创建了一个包含一个整数和一个列表的列表,并使用deepcopy()方法将其深拷贝到了另一个变量中。
import copylist1 = [1, 2, [3, 4]]
list2 = copy.deepcopy(list1)print(list2) # [1, 2, [3, 4]]# 深拷贝的工作原理:
import copylist1 = [1, 2, [3, 4]]
list2 = copy.deepcopy(list1)print("list1:", list1) # list1: [1, 2, [3, 4]]
print("list2:", list2) # list2: [1, 2, [3, 4]]list1[2][0] = 5 # 修改原始列表中的嵌套列表时,新列表中的相应元素没有被修改。
print("list1:", list1) # list1: [1, 2, [5, 4]]
print("list2:", list2) # list2: [1, 2, [3, 4]]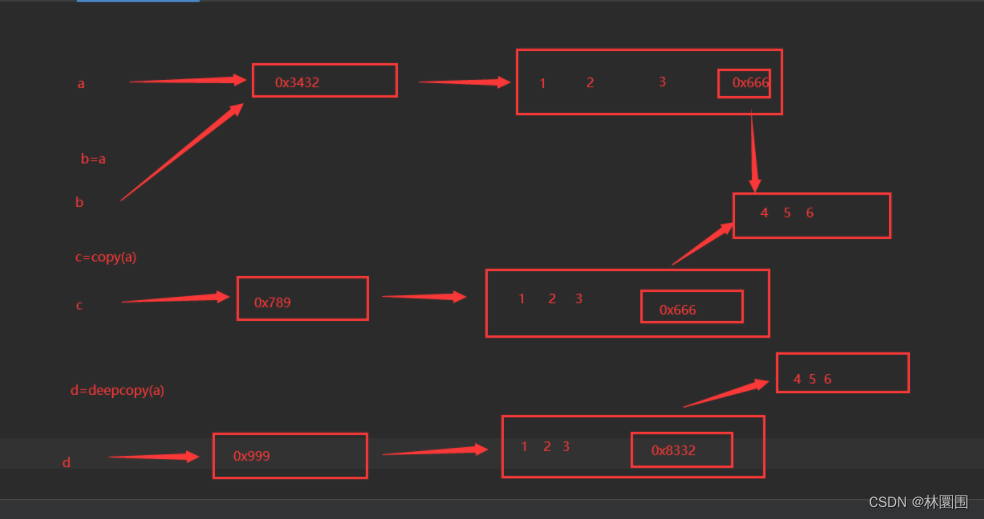
3.3 扩展(slice操作符和list构造函数)
1 slice操作符slice操作符可以用于复制列表、元组、字符串等序列类型的对象。例如:a = [1, 2, 3, 4]b = a[:]这里,b就是a的一个浅拷贝,它包含了a中所有元素的副本。由于slice操作符只进行浅拷贝,因此如果a中包含了嵌套的对象,那么b中的这些对象仍然是a中的引用。2. list()构造函数list()构造函数可以用于将其他序列类型的对象转换为列表,并且可以实现浅拷贝。例如:a = (1, 2, 3, 4)b = list(a)这里,b就是a的一个浅拷贝,它包含了a中所有元素的副本。另外,需要注意的是,Python中的一些内置类型,如int、str、tuple等是不可变类型,它们没有提供
修改自身内容的方法。因此,对这些类型进行浅拷贝和深拷贝是没有任何区别的。例如:a = 123b = copy.copy(a)c = copy.deepcopy(a)这里,b和c都是a的副本,它们的值都是123。最后,需要注意的是,在Python中,对象的复制和对象的赋值是不同的概念。
对象的赋值只是将一个变量名与一个对象关联起来,而不是复制对象本身。例如:a = [1, 2, 3]
b = a
这里,b只是a的一个别名,它们实际上指向同一个对象。因此,对a或b进行修改,都会影响到另一个变量。
如果需要复制a的副本,可以使用a.copy()或者copy模块中的函数。
3.4 深入理解赋值、浅copy、深copy
## 赋值
a = [1, 2, 3, [5, 6, 67]]
b = a # 赋值,没有涉及到copy
print(b) # [1, 2, 3, [5, 6, 67]]b[0] = 99
# 只要改b的任何位置,a都会跟着改
print(b) # [99, 2, 3, [5, 6, 67]]
print(a) # [99, 2, 3, [5, 6, 67]]## 浅copy
from copy import copya = [1, 2, 3, [5, 6, 67]]
c = copy(a)
c[0] = 999
print(c) # [999, 2, 3, [5, 6, 67]]
# 如果是不可变类型,不会影响
print(a) # [1, 2, 3, [5, 6, 67]]# 如果是可变类型
c[3][1] = 666
print(c) # [999, 2, 3, [5, 666, 67]]
print(a) # [1, 2, 3, [5, 666, 67]]## 深copy
from copy import deepcopya = [1, 2, 3, [5, 6, 67]]
d = deepcopy(a)
d[0] = 999
print(d) # [999, 2, 3, [5, 6, 67]]
# 如果是不可变类型,不会影响
print(a) # [1, 2, 3, [5, 6, 67]]# 如果是可变类型
d[3][1] = 666
print(d) # [999, 2, 3, [5, 666, 67]]
print(a) # [1, 2, 3, [5, 6, 67]]