单纯做网站的公司ui设计属于视觉传达吗
Cesium 实战 - 使用 gltf-vscode 查看、预览以及编辑 glTF 和 GLB 模型
- VScode(Visual Studio Code) 安装模型必要插件
- VScode 预览自定义关节(articulations)动作
- VScode 导入 GLB 格式模型
- VScode 导出 GLB 格式模型
模型渲染作为 Cesium 一个非常重要的功能,目前只支持 glTF 和 GLB 两种格式,其实是一种格式,GLB 是 glTF 的二进制形式。
在实际项目中,由于对模型的操作,可能会需要查看模型的属性。之前一直使用 blender 来查看、调整以及转换等操作。模型转换详见:Cesium 三维模型使用 blender 调整位置、坐标轴、比例等。
近期有需求,需要给模型增加 自定义关节(articulations)动作,然后发现 blender 对于 Cesium 开发人员不太友好,尤其是查看 glTF 的 json 数据属性。
后来发现一个开源项目,可以直接查看和操作 glTF 模型:gltf-vscode。
gltf-vscode 是由 AGI(一家美国工程仿真领域的企业) 开发和维护的,功能非常强大,比较适合 Cesium 开发人员。
gltf-vscode 可以查看编辑模型、导入 GLB 模型、GLB 与 glTF 转换等功能。
本文包含 VScode 安装模型必要插件、预览自定义关节动作、导入 GLB 格式模型、导出 GLB 格式模型 四部分。
VScode(Visual Studio Code) 安装模型必要插件
Visual Studio Code 下载于安装比较简单,也不需要破解,不过多介绍。
使用 VScode 打开 gltf-vscode 项目。
VScode 应该会自动提示安装所需插件:
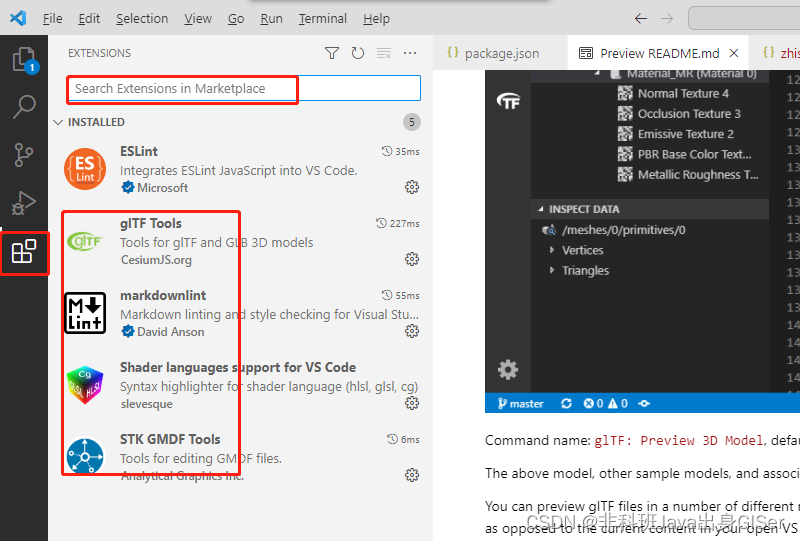
复制 glTF 模型到项目中,这里作者新建 public/model 文件夹来存放模型。
预览 glTF 模型,可以查看 glTF 文件数据以及预览模型:
注意:需要打开 glTF 模型文件之后,在文件内右键操作。
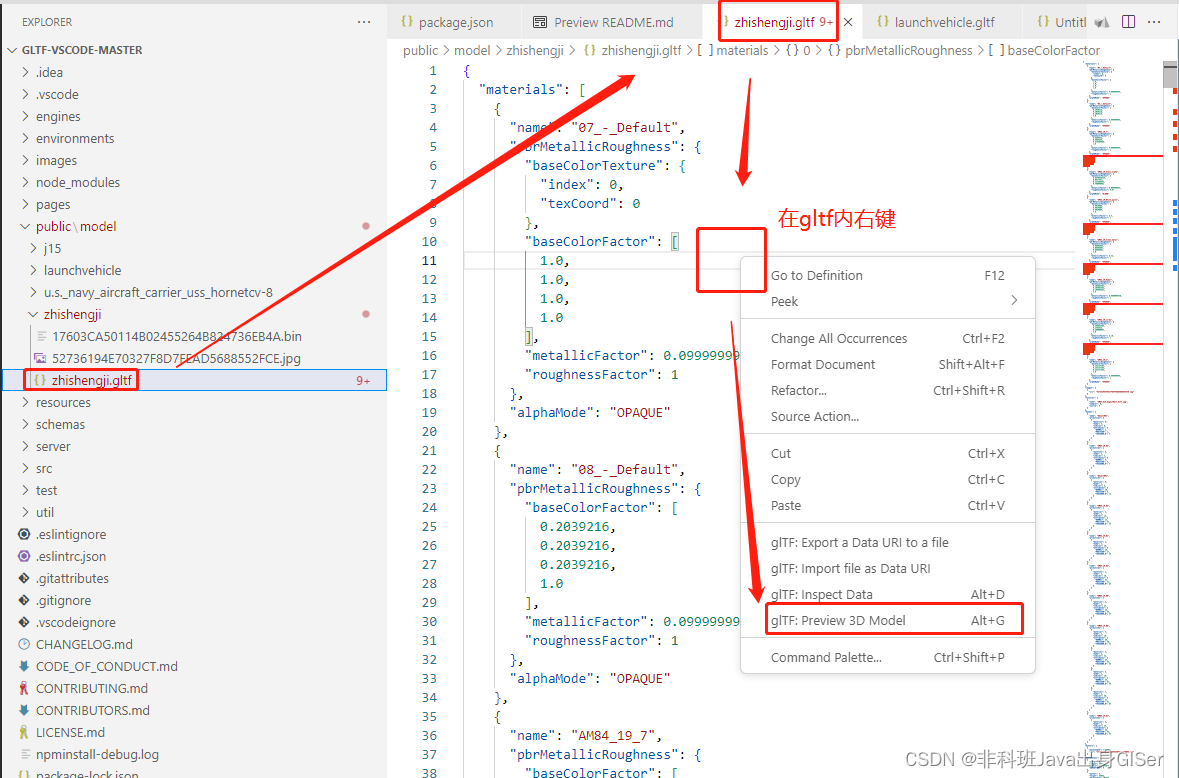
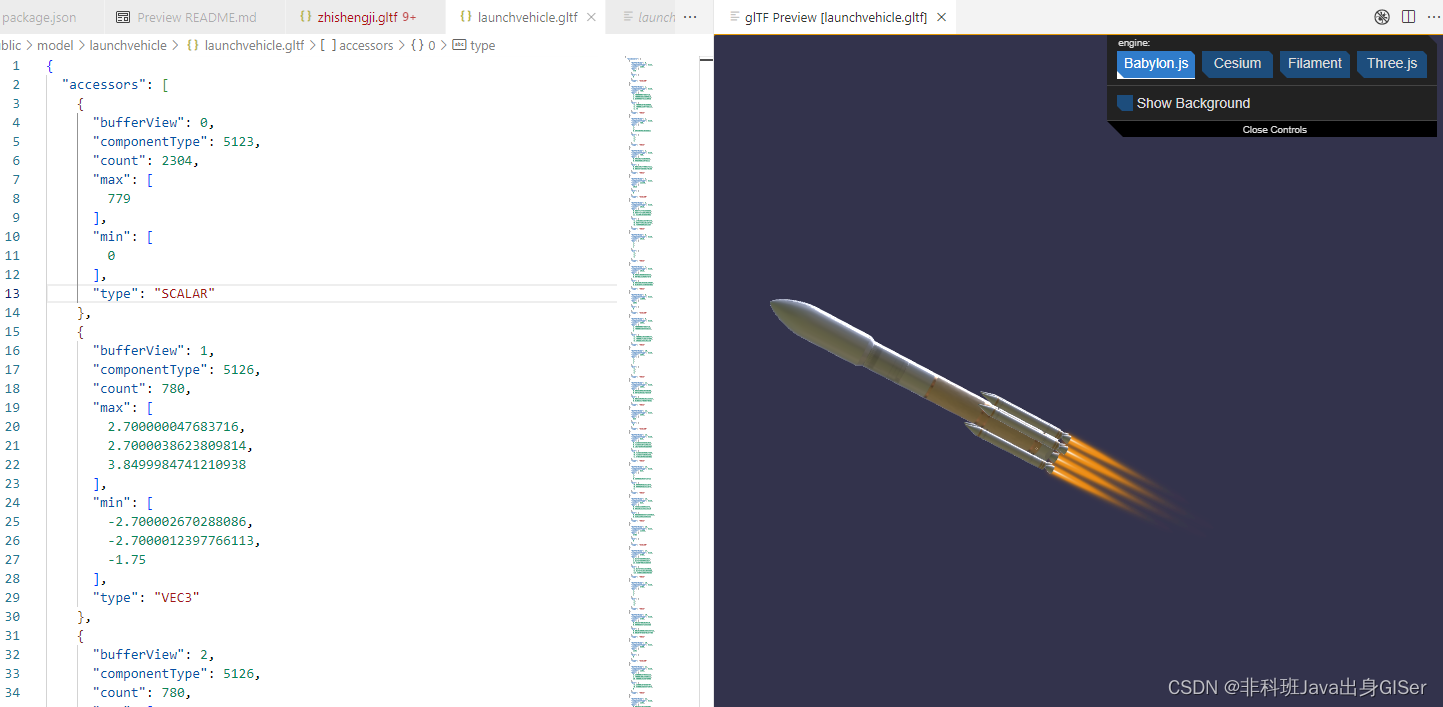
默认为 Babylon 渲染模型,这里也可以切换其他模型预览引擎:
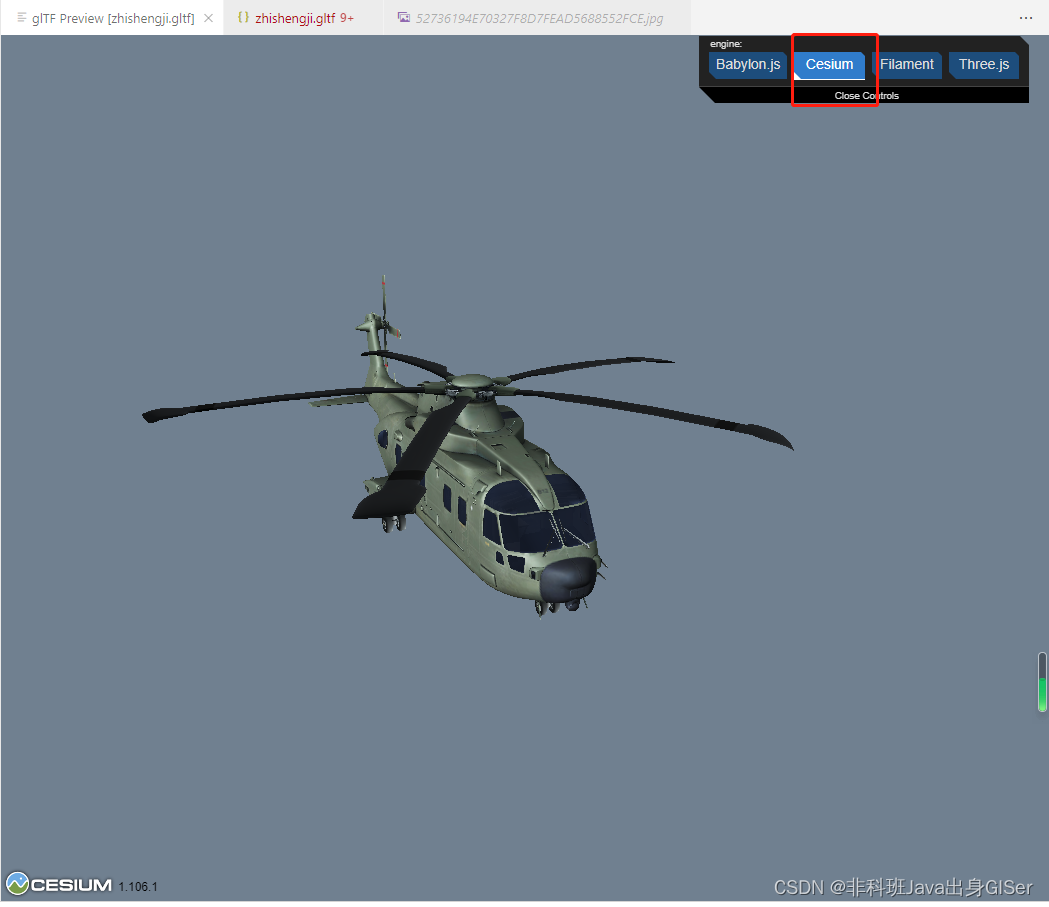
以下为 Cesium 官方火箭推进器的模型(cesium.vip 镜像源):
launchvehicle.gltf
launchvehicle.glb
VScode 预览自定义关节(articulations)动作
预览切换为 Cesium 引擎时,可以查看模型自定义的关节(articulations)动作:
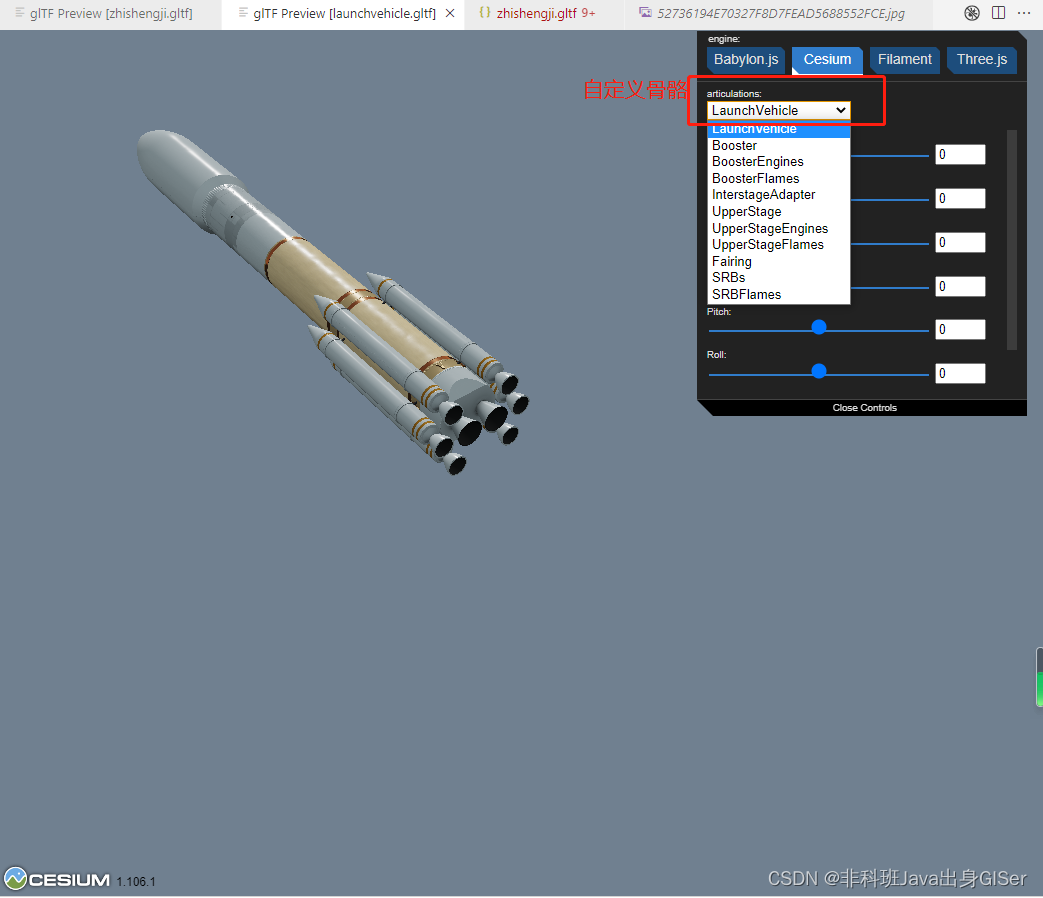
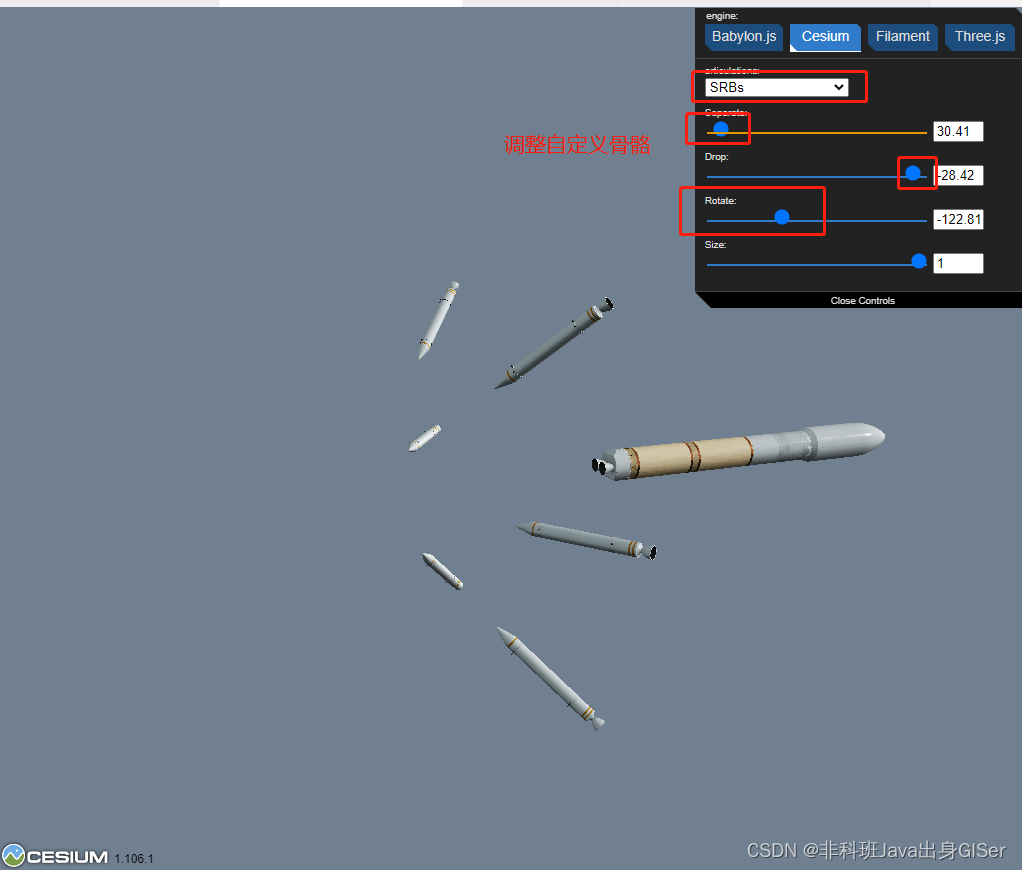
这里选择了 SRB 固体助推器模块组件,并且调整 Separate、Drop 和 Rotate 关节(articulations)参数来查看效果:
VScode 导入 GLB 格式模型
GLB 模型为二进制文件,VScode 不能直接打开,这里演示导入 GLB 格式模型:
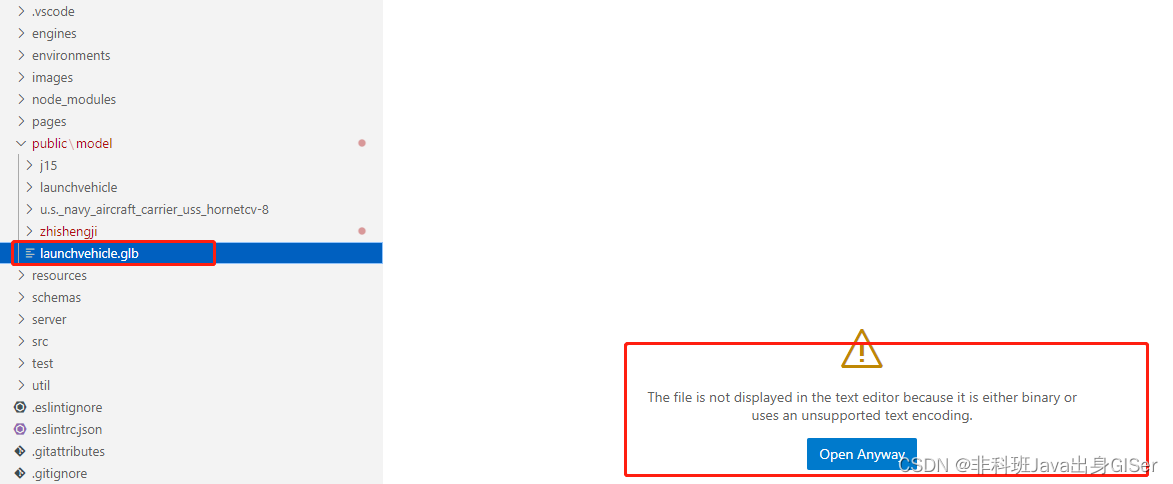
将 GLB 文件拷贝到项目中:

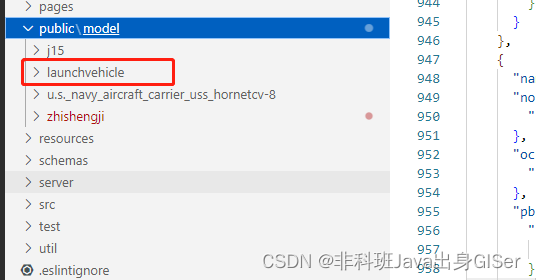
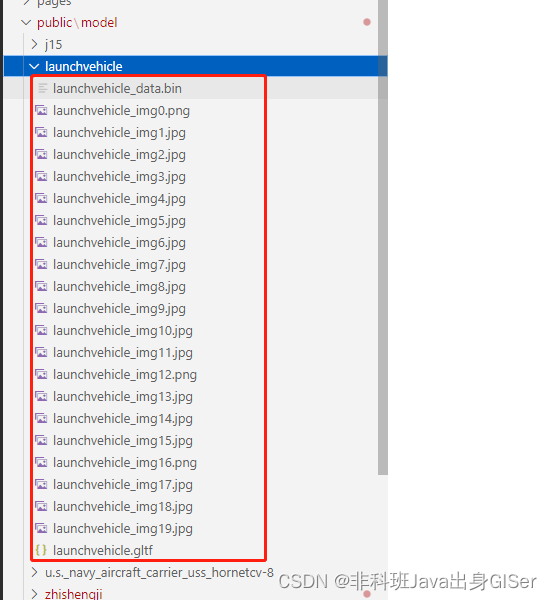
由于 GLB 模型转为 glTF 格式,会生成一系列相关文件,这里创建文件夹用于存放这些文件:
选中 GLB 模型,右键 - 导入 GLB 模型(glTF: Import from GLB):
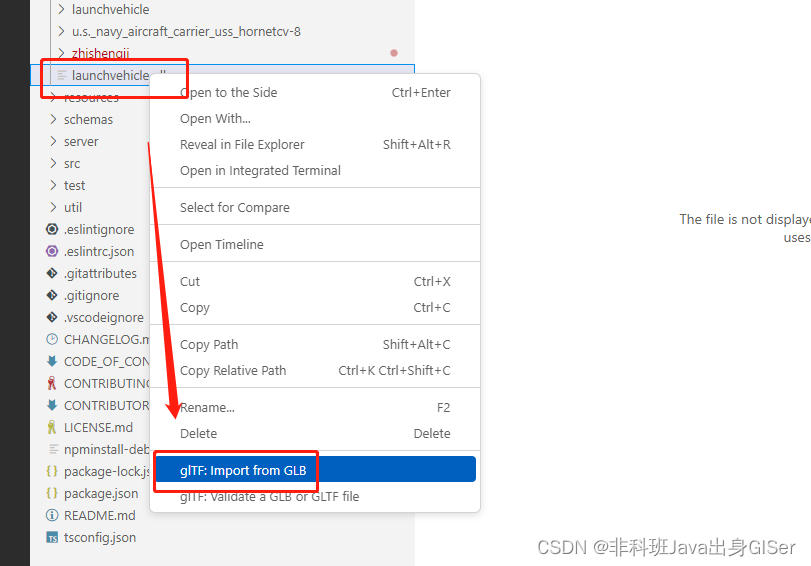
选择创建好的文件夹,这里不建议修改名字,保存:
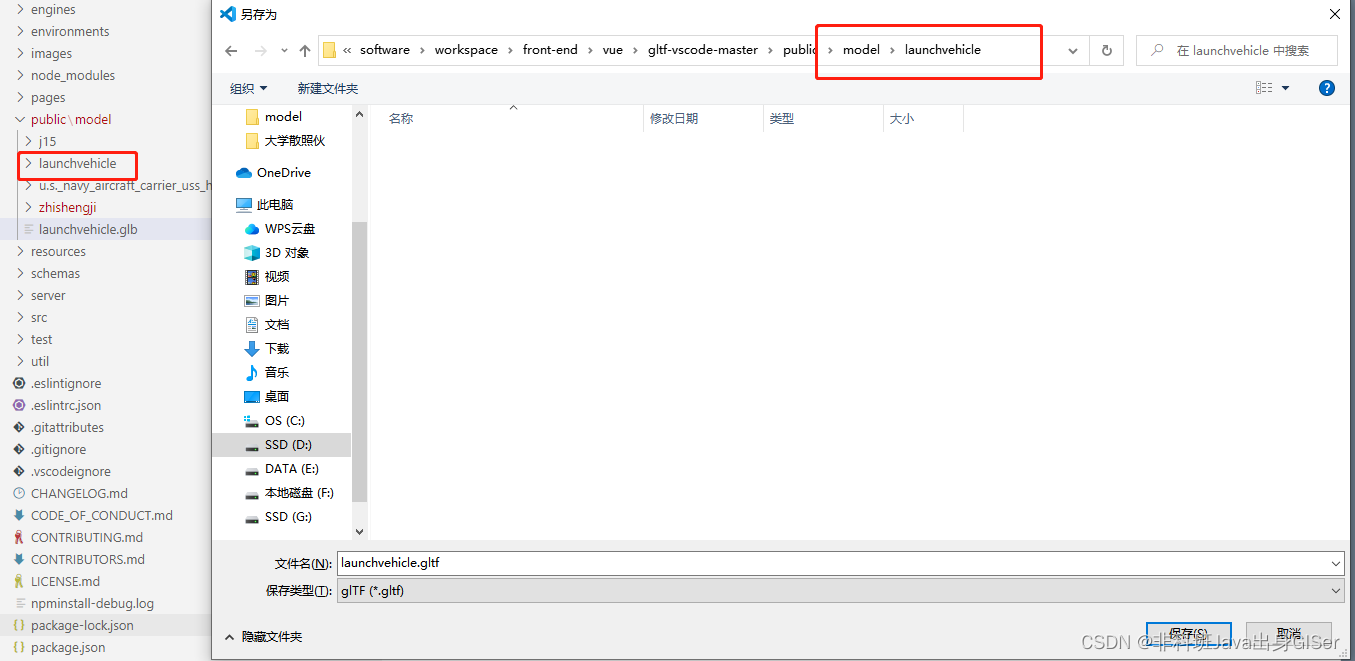
以下是生成的 glTF 模型以及相关文件(所有文件均不可删除,否则会出问题):
点击 glTF 文件,查看内容以及预览模型:
VScode 导出 GLB 格式模型
glTF 格式模型更方便编辑,但是松散的 glTF 模型(包含 .bin、.jpg 等)不容易移动使用,可以导出为 GLB 格式:
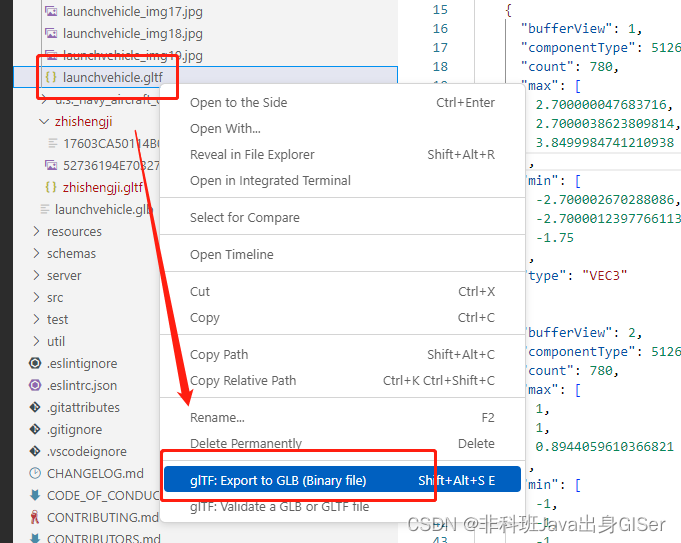
导出之后,在 Cesium 中加载使用:

参考博客:
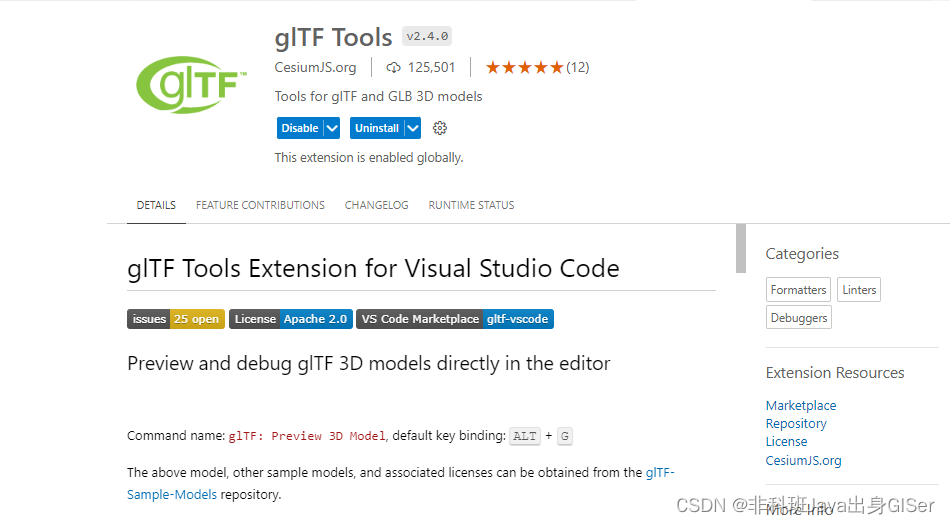
[1]: glTF Tools Extension for Visual Studio Code
[2]: VSCode查看gltf文件(glTF Tools插件)
[3]: 图形化开发(六)03-Three.js之导入模型——glTF格式文件导入,3D模型的使用 & vs code之glTF Tools插件的使用方法
[4]: 3D性能优化 | 说一说glTF文件压缩
