佛山新网站建设服务公司wordpress qq空间模板
【QT5-自我学习-线程qThread练习-两种使用方式-2:通过继承Qobject类-自己实现功能函数方式-基础样例】
- 1、前言
- 2、实验环境
- 3-1、学习链接-参考文章
- 3-2、先前了解-自我总结
- (1)线程处理逻辑事件,不能带有主窗口的事件
- (2)一般考虑使用的时候,是当你发现,主窗口会有卡顿,需要线程在后台来处理。
- (1)通过继承QOject类这种方式-特点。
- 4、实验过程
- (0)实验目标
- (1)新建工程
- (2)UI布局
- (3)线程类代码编写
- (4)编写mainwindow.cpp内容。
- 5-1、实际效果
- 5-2、代码链接
- 6、细节部分
- (1)同样的,main.cpp加入一段声明代码。
- 7、总结
1、前言
学习线程其实有一段时间了,当时只是学习,没有实际用起来,最近做的一个qt程序,发现如果不使用线程,那么就会导致界面卡死,这样才体现出线程的实际作用。
这里是第二章,第二种实现线程方式,这个还是和继承线程类的方式不太一样的,两种本身没有优劣之分,看你使用场景与习惯。
2、实验环境
实验环境还是挺重要的,因为有时候,在你电脑上能运行的东西,在别人的电脑就不一定能运行,这一部分的原因就可能是实验版本不一样。
系统环境:window环境
QT软件版本:qt 5.14.2
ST-Link命令行工具的版本号:STM32 ST-LINK CLI v3.6.0.0
3-1、学习链接-参考文章
自己也是参考他人文章,通过学习他人的文章与视频学习了qt多线程,当然要说明出处。
如下是博客地址,里面相关概念总结:https://subingwen.cn/qt/thread/
如下是B站上视频,也是通过视频,敲的代码:https://www.bilibili.com/video/BV1iN411f7dY/?spm_id_from=333.337.search-card.all.click&vd_source=631b10b31b63df323bac39281ed4aff3
3-2、先前了解-自我总结
博客文章说得已经非常好了,自己也会重新总结下。
(1)线程处理逻辑事件,不能带有主窗口的事件
线程可以在后台辅助你,对一些数据进行除了,但是对于主界面的控件等,不能直接控制,从使用来说,
以下是一个例子,不能直接使用以下方式来调用界面的控件。
ui->label->setText("data");
当然是可以通过一些信号与槽,或者全局变量的方式来传递数据。
(2)一般考虑使用的时候,是当你发现,主窗口会有卡顿,需要线程在后台来处理。
自己本次使用的时候,是因为碰到st-link烧写,并且文件很大的时候,主界面会直接卡住,才考虑使用,而不要是为了使用而使用,当你觉得主界面太卡,并且可以放在后台执行的时候,那么你就可以开一个线程。
(1)通过继承QOject类这种方式-特点。
1、对比继承线程类方式,这种一个显著特定,没有run这个函数了,你自己写自定义函数,到时候直接调用就可以了。
2、编写自定义函数内容
我们很多时候,是先学习怎么去做,然后返回来在具体了解内部细节的。
4、实验过程
(0)实验目标
采用两种不同速度排序的方式,对一个乱序的数组进行排序,这个过程中,需要生产乱序数组,使用一个线程,两种排序需要使用两个线程,所有一种有3个线程。
(1)新建工程
新建工程,是qtk开始的步骤,至少先让你的空白模块跑起来,如下,这里就不过多叙述了(这里直接使用之前图片了)。
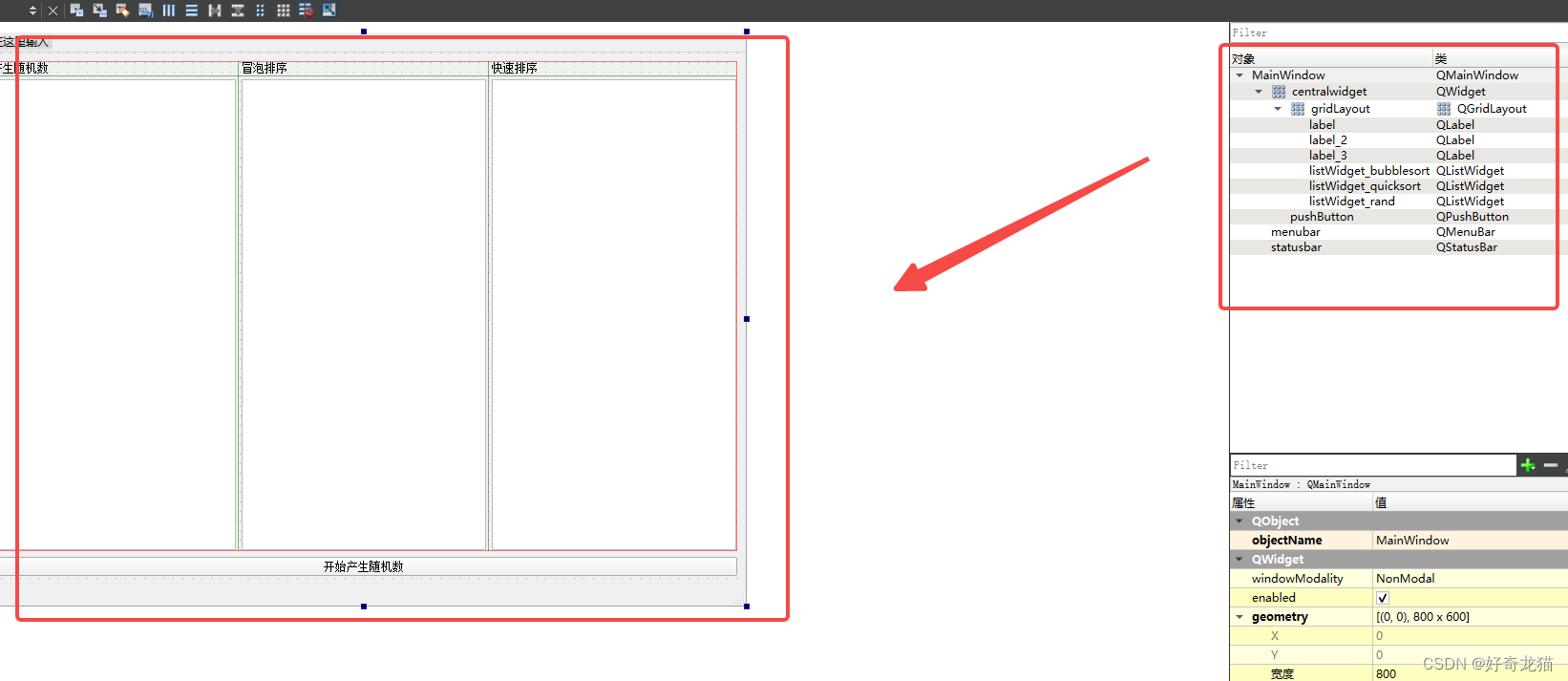
(2)UI布局
我们需要是三个框,也就是listWidget,分别放置三个数组,一个是乱序数组,另外两个是冒泡排序和快排,如下。
(3)线程类代码编写
本工程就不在分太多文件了,只是添加一个线程文件,将三个线程写在一起。
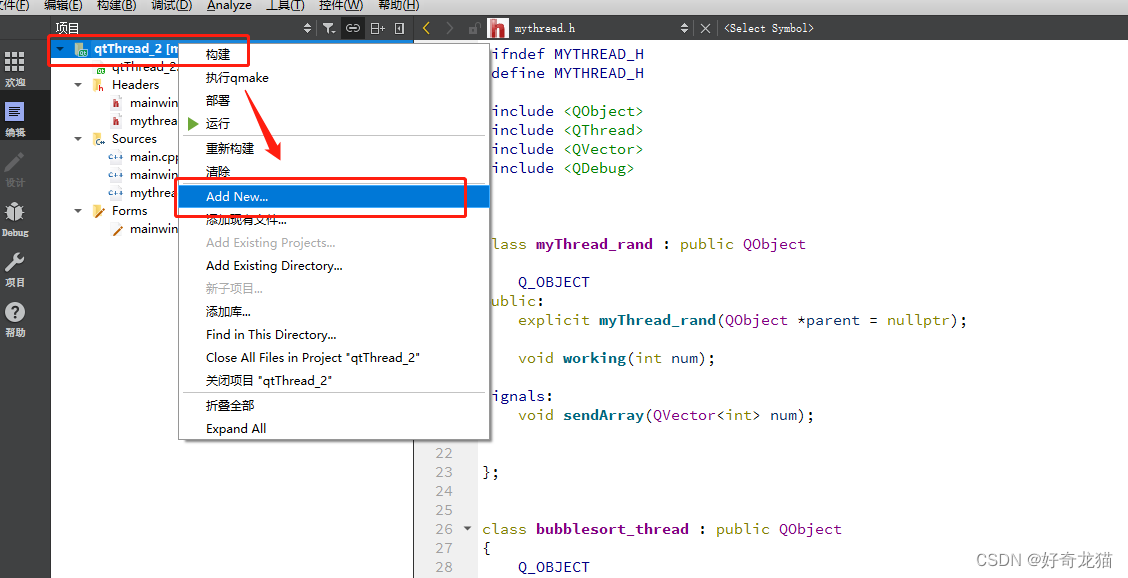
(1)添加新的文件,在项目上右键,然后选择“Add New…”
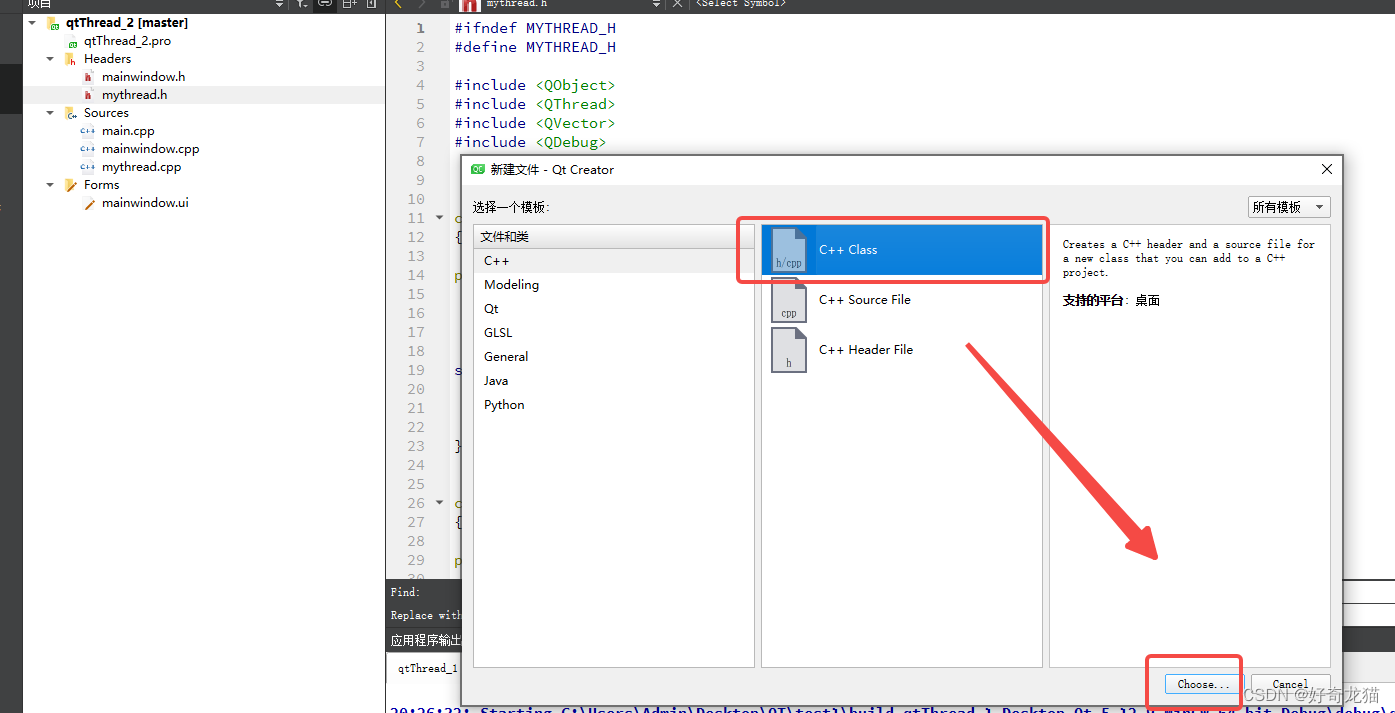
(2)添加新的C++文件,然后命名,
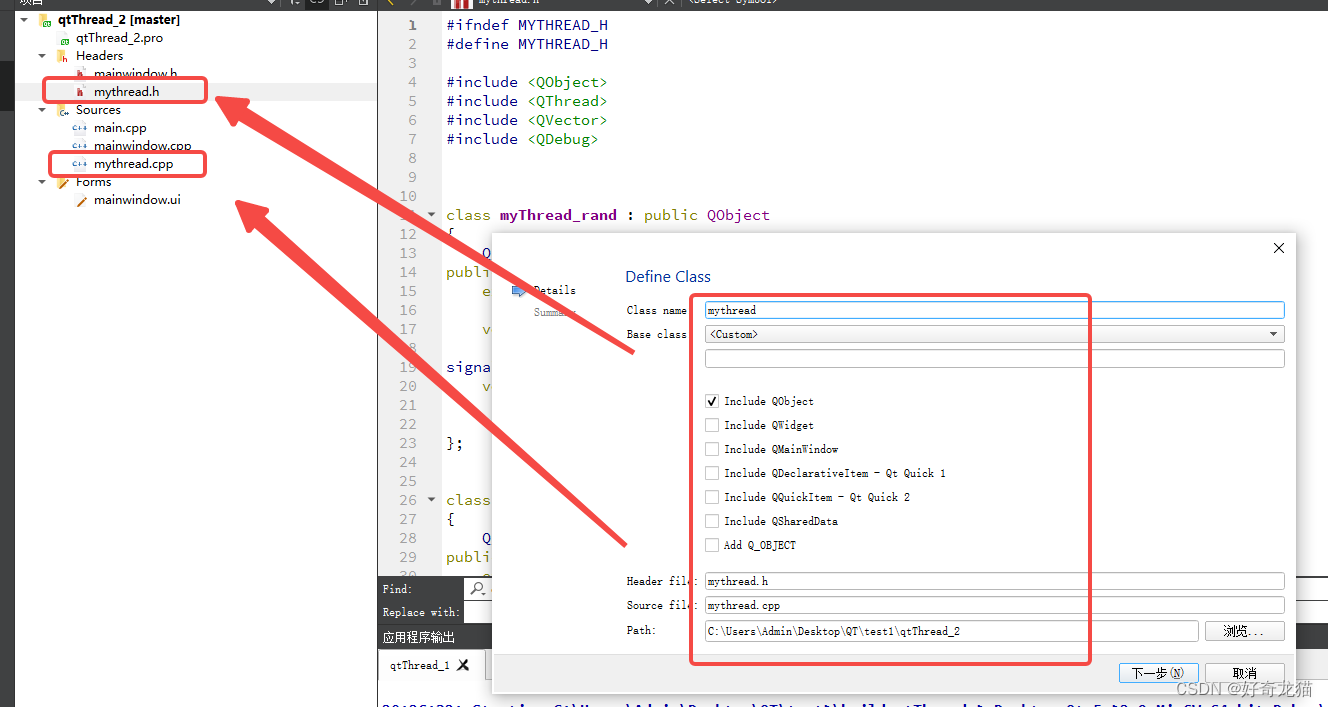
(3)这里可以先选上include QObject,细节代码,我们稍后添加。
(4)编写对于”mythread.h“和“mythread.cpp”内容。
我们需要继承QObject类,编写功能函数声明,自定义函数声明的,如下代码快,
#ifndef MYTHREAD_H
#define MYTHREAD_H#include <QObject>
#include <QThread>
#include <QVector>
#include <QDebug>class myThread_rand : public QObject
{Q_OBJECT
public:explicit myThread_rand(QObject *parent = nullptr);void working(int num);signals:void sendArray(QVector<int> num);};class bubblesort_thread : public QObject
{Q_OBJECT
public:explicit bubblesort_thread(QObject *parent = nullptr);void working(QVector<int> list);signals:void finish(QVector<int> num);};class quickSort_thread : public QObject
{Q_OBJECT
public:explicit quickSort_thread(QObject *parent = nullptr);
//任务函数void working(QVector<int> list);signals:void finish(QVector<int> num);};#endif // MYTHREAD_H“mythread.cpp”内容,主要是实现相应函数内容,具体实现内容,这里也直接给出代码块。
#include "mythread.h"
#include <QElapsedTimer>
#include <QThread>using namespace std;myThread_rand::myThread_rand(QObject *parent) : QObject(parent)
{}bubblesort_thread::bubblesort_thread(QObject *parent) : QObject(parent)
{}quickSort_thread::quickSort_thread(QObject *parent) : QObject(parent)
{}void myThread_rand::working(int num)
{qDebug() << "生成随机数的线程地址为:" << QThread::currentThread() << endl;QVector<int> list;QElapsedTimer time;time.start();for(int i=0;i<num;++i){list.push_back(qrand()%10000);}int milsec = time.elapsed();qDebug() << "生成" << num<< "个随机总数用时:"<< milsec <<"毫秒" <<endl;emit sendArray(list);
}void bubblesort_thread::working(QVector<int> list)
{qDebug() << "冒泡生成的线程地址为:" << QThread::currentThread() << endl;QElapsedTimer time;time.start();// QVector<int> list;int temp;for(int i=0;i<list.size();++i){for(int j=0;j<list.size()-i-1;++j){if(list[j]>list[j+1]){temp=list[j];list[j]=list[j+1];list[j+1]=temp;}}}int milsec = time.elapsed();qDebug() << "冒泡总数用时:"<< milsec <<"毫秒" <<endl;emit finish(list);
}void quickSort_thread::working(QVector<int> list)
{qDebug() << "快速排序的线程地址为:" << QThread::currentThread() << endl;QElapsedTimer time;time.start();// QVector<int> list;std::sort(list.begin(),list.end());int milsec = time.elapsed();qDebug() << "快速排序总数用时:"<< milsec <<"毫秒" <<endl;emit finish(list);
}(4)编写mainwindow.cpp内容。
这里的工作,主要是创建子线程,并传递数据,具体可以直接参照代码。
#include "mainwindow.h"
#include "ui_mainwindow.h"
#include <QThread>
#include "mythread.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow)
{ui->setupUi(this);//1.创建子线程QThread* t1 = new QThread;QThread* t2 = new QThread;QThread* t3 = new QThread;//2.创建任务类的对象myThread_rand* gen = new myThread_rand;bubblesort_thread* bubble = new bubblesort_thread;quickSort_thread* quick = new quickSort_thread;//3.将任务对象转移到每个子线程中gen->moveToThread(t1);bubble->moveToThread(t2);quick->moveToThread(t3);//4 按下按键 启动随机数线程connect(ui->pushButton,&QPushButton::clicked,this,[=](){emit starting(10000);t1->start();});//5 连接到产生随机数据函数,开始产生随机数据connect(this,&MainWindow::starting,gen,&myThread_rand::working);connect(gen,&myThread_rand::sendArray,bubble,&bubblesort_thread::working);connect(gen,&myThread_rand::sendArray,quick,&quickSort_thread::working);connect(gen,&myThread_rand::sendArray,this,[=](QVector<int> list){t2->start();t3->start();for(int i=0;i<list.size();++i){ui->listWidget_rand->addItem(QString::number(list.at(i)));}});connect(bubble,&bubblesort_thread::finish,this,[=](QVector<int> list){for(int i=0;i<list.size();++i){ui->listWidget_bubblesort->addItem(QString::number(list.at(i)));}});connect(quick,&quickSort_thread::finish,this,[=](QVector<int> list){for(int i=0;i<list.size();++i){ui->listWidget_quicksort->addItem(QString::number(list.at(i)));}});
}MainWindow::~MainWindow()
{delete ui;
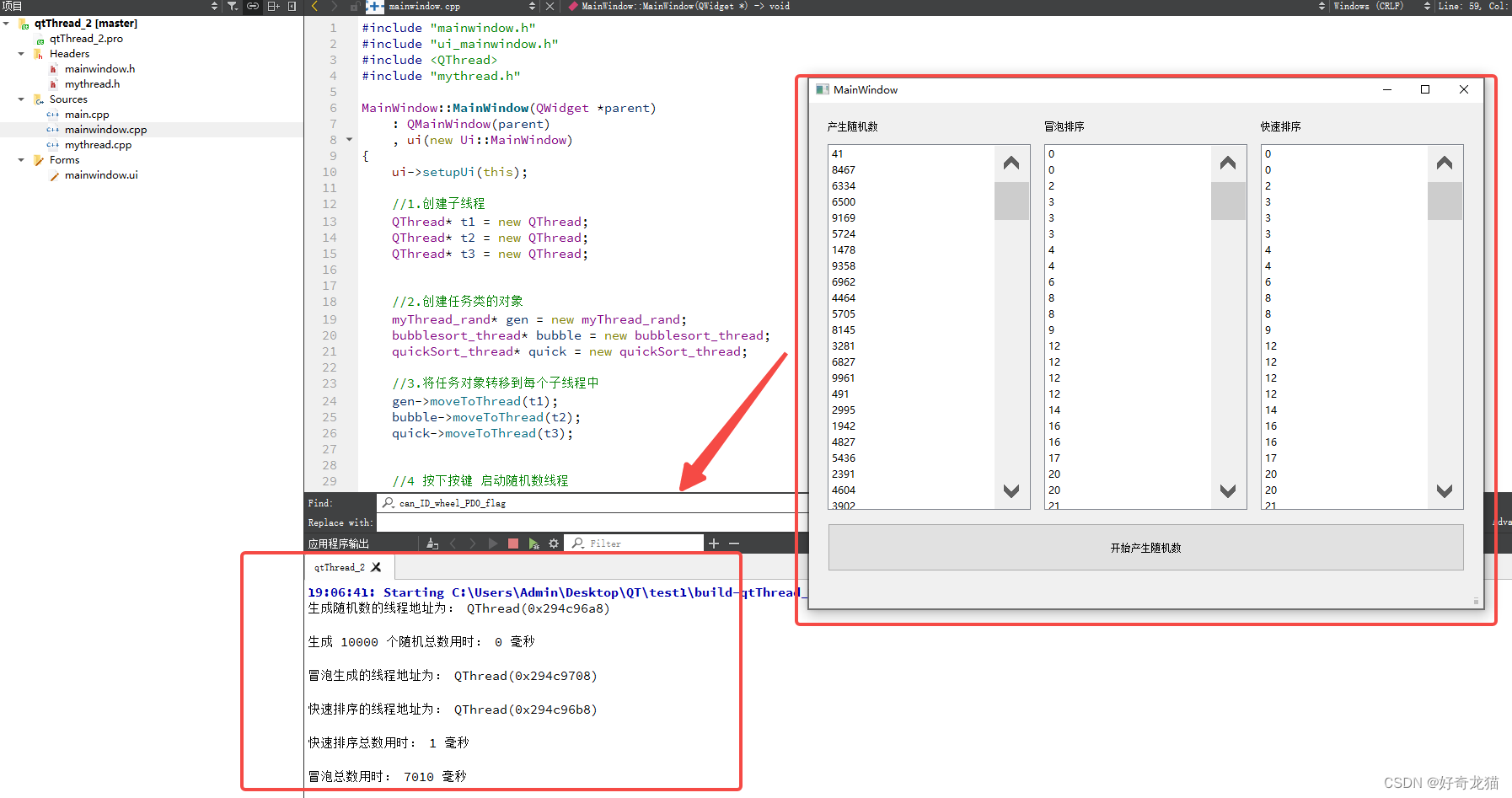
}5-1、实际效果
实际效果如下,还是可以看到,不同算法,排序实际确实不是一样的。
5-2、代码链接
代码链接:https://download.csdn.net/download/qq_22146161/88245843
6、细节部分
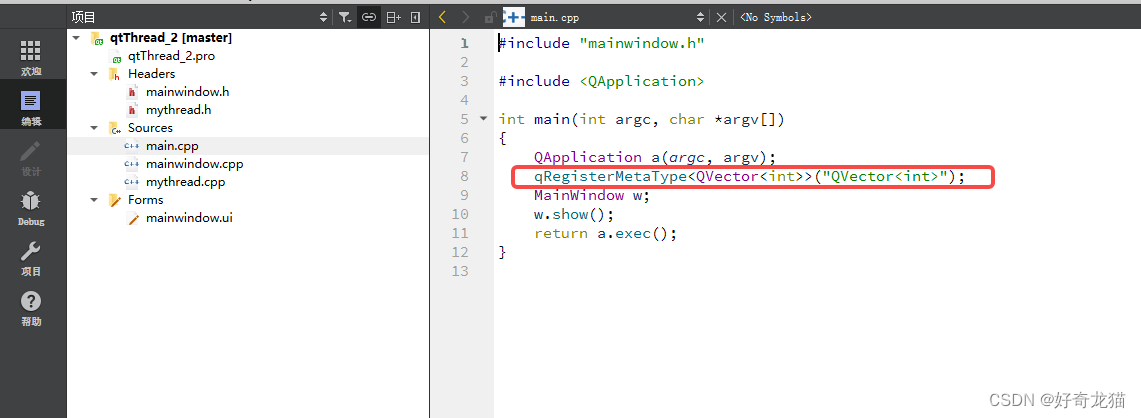
(1)同样的,main.cpp加入一段声明代码。
根据博主说明,要在main.cpp加入一段声明代码,否则会有错误。
7、总结
这里只是实现不一样,所有文章很多部分和第一篇有些类似。后续会加入一篇讲解关于移植部分。
