网站流量 seo商丘网络推广平台
前面的文章,我们描述了网络是怎样进行传输数据包的,但是网络是不安全的,对于这种流量门户网站其实还好,对于支付类场景其实容易将数据泄漏,所以安全的方式是通过加密,加密方式主要是对称加密和非对称加密。
对称加密,其实就是双方使用同样的密钥进行加解密。而非对称加密方式是会生成两对公私密钥。
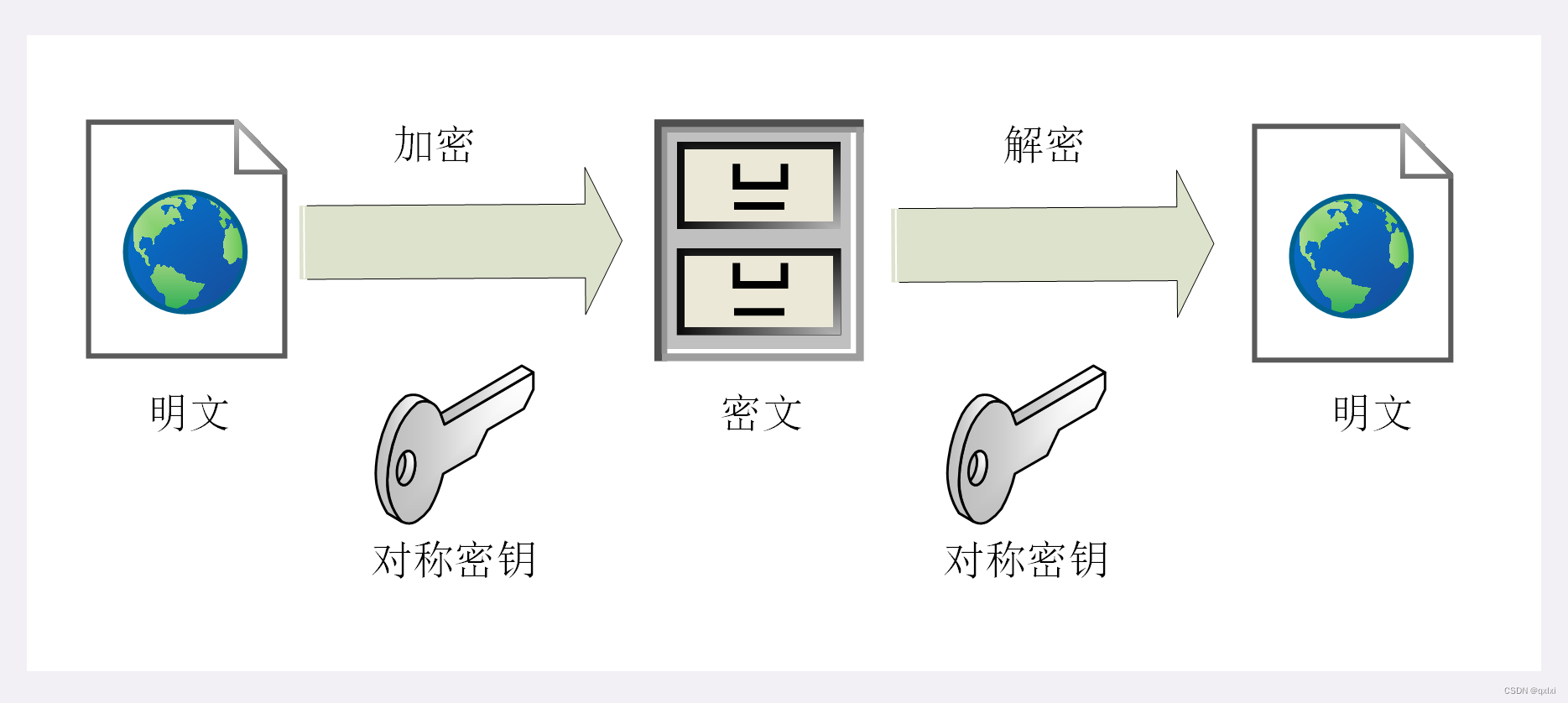
对称加密
因为对称加密,需要进行先传输密钥,所以这种如果在网络上进行其实容易泄漏,最好的方式其实就是使用线下传输,之前还经历过,一次商务拿着对方的密钥进行线下邮件传输的。但是对于互联网来说,其实是不合理的,所以最好的方式就是非对称加密。
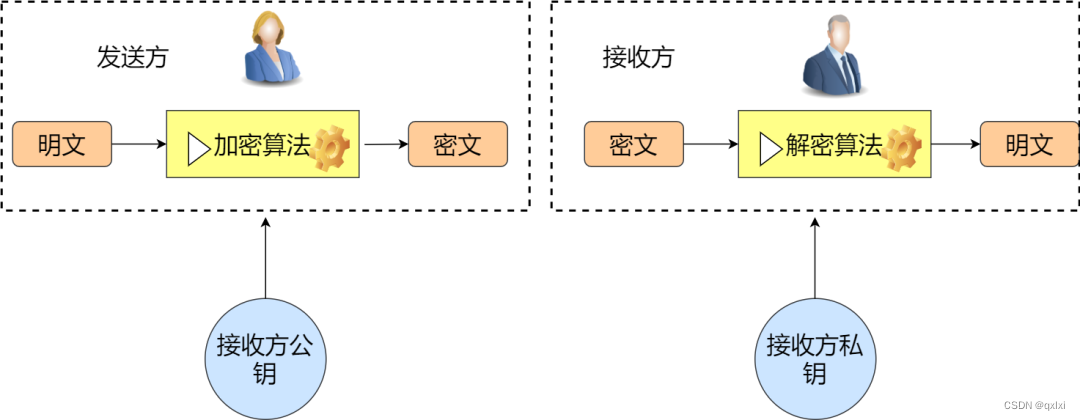
非对称加密
其实就是发送方和接收方都有自己都公钥和私钥,发送方用自己的私钥进行加密,接收方使用发送方的公钥解密。接收方使用自己的私钥进行加密,发送方使用接收方的公钥进行解密。
HTTPS 的工作模式
HTTPS 协议的总体思路 公钥私钥主要用于传输对称加密的秘钥,而真正的双方大数据量的通信都是通过对称加密进行的
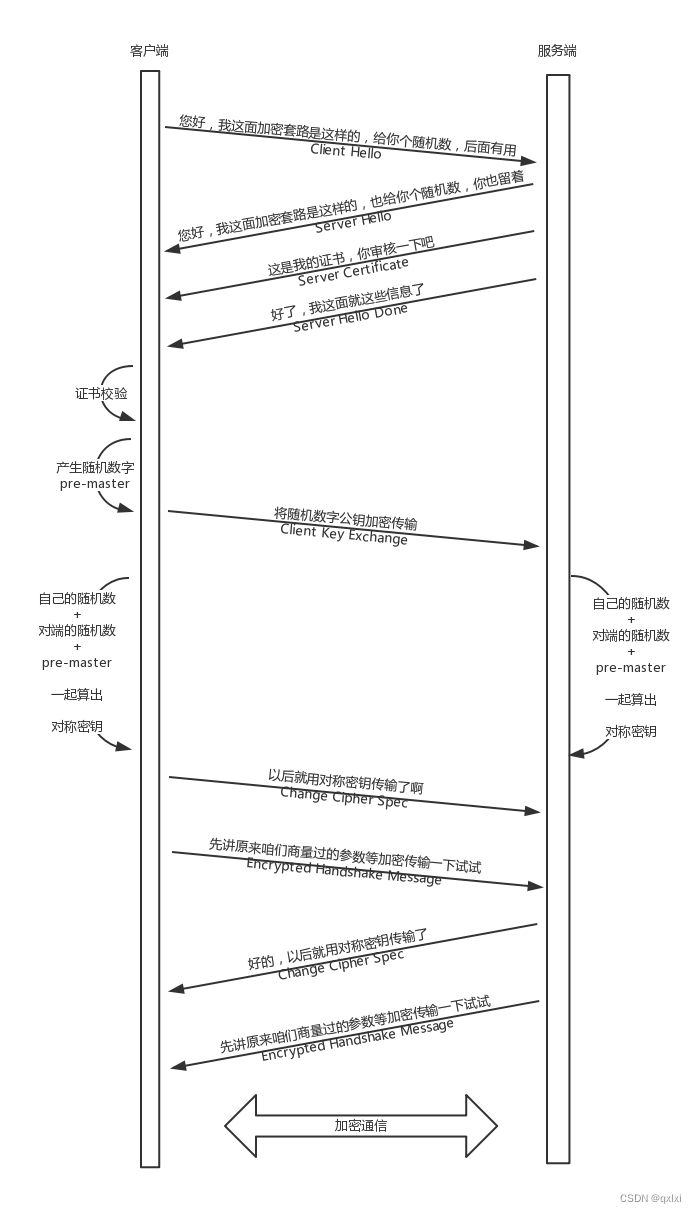
https 其实是由两部分组成:http+ssl/tls,也就是在 http 上又加了一层处理加密信息的模块,服务端和客户端的信息传输都会通过 tls 加密,传输的数据都是加密后的数据。加解密过程:
1)客户端发起 https 请求(就是用户在浏览器里输入一个 https 网址,然后连接到 server的 443 端口)
2)服务端的配置(采用 https 协议的服务器必须要有一塔数字证书,可以自己制作,也可以向组织申请,这套证书就是一对公钥和私钥)。
3)传输证书(这个证书就是公钥,只是包含了很多信息)
4)客户端解析证书(由客户端 tls 完成,首先验证公钥是否有效,若发现异常,则弹出一个警示框,提示证书存在问题,若无问题,则生成一个随机值,然后用证书对随机值进行加密)
5)传输加密信息(这里传输的是加密后的随机值,目的是让服务端得到这个随机值,以后客户端和服务端的通信就可以通过这个随机值来进行加密了)
6)服务端解密信息(服务端用私钥解密后得到了客户端传来的随机值,then 把内容通过该值进行对称加密。所谓对称加密就是,将信息和私钥通过某种算法混在一起,这样除非知道私钥,不然无法获取内容,而正好客户端和服务端都知道这个私钥,所以只要加密算法够彪悍,私钥够复杂,数据就够安全)
7)传输加密的信息
8)客户端解密信息,用随机数来解。
HTTP与HTTPS的理解 区别?
HTTP是超文本传输协议,数据明文传输,HTTPS在HTTP的基础上加入了SSL协议,实现数据的加密传输。
HTTPS需要去申请证书,一般是收费的。
HTTP默认使用80端口,HTTPS默认使用443端口。
小结
加密分对称加密和非对称加密。对称加密效率高,但是解决不了密钥传输问题;非对称加密可以解决这个问题,但是效率不高。
非对称加密需要通过证书和权威机构来验证公钥的合法性。
HTTPS 是综合了对称加密和非对称加密算法的 HTTP 协议。既保证传输安全,也保证传输效率
