徐汇制作网站哪家好华为免费企业网站建设
服务器RAID配置及功能介绍
- 一、RAID磁盘阵列详解
- 1.RAID磁盘阵列介绍
- 2.RAID 0
- 3.RAID1
- 4.RAID3
- 5.RAID5
- 6.RAID6
- 7.RAID 10
- 总结
- 阵列卡介绍
一、RAID磁盘阵列详解
1.RAID磁盘阵列介绍
-
①是Redundant Array of lndependent Disks的缩写中文简称为独立冗余磁盘阵列。
-
②把多块独立的物理硬盘按不同的方式组合起来形成一个硬盘组(逻辑硬盘),从而提供比单个硬盘更高的存储性能和提供数据备份技术。
-
③组成磁盘阵列的不同方式称为RAID级别(RAID Levels)。
-
④常用的RAID级别
-
RAID0,RAID1,RAID5,RAID6,RAID1+0等
2.RAID 0
-
①RAID 0连续以位或字节为单位分割数据,并行读/写于多个磁盘上,因此具有很高的数据传输率,但它没有数据冗余。
-
②RAID 0只是单纯地提高性能,并没有为数据的可靠性提供保证,而且其中的一个磁盘失效将影响到所有数据。
-
③RAID 0 最少需要两块磁盘。
3.RAID1
-
①通过磁盘数据镜像实现数据冗余,在成对的独立磁盘上产生互为备份的数据。
-
②当原始数据繁忙时,可直接从镜像拷贝中读取数据,因此RAID 1可以提高读取性能。
-
③RAID1 最少需要两块磁盘,安全性高,但是磁盘利用率很低
4.RAID3
- ①假如有三块1T硬盘,其中一块硬盘用于校验数据,另外剩下两块组成RAID0模式,这样三块硬盘就能有2T空间
- ②提升了硬盘速度,也不会像 RAID0那么容易坏,而且专门有一块硬盘专门用于数据校验
- ③这种模式最少需要三块硬盘,最多只能允许一个硬盘损坏,但是如果这个数据校验盘坏了,数据就全部丢失了,这种模式用的也比较少
5.RAID5
-
①N(N>=3)块盘组成阵列,一份数据产生N-1个条带,同时还有1份校验数据,共N份数据在N块盘上循环均衡存储。
-
②N块盘同时读写,读性能很高,但由于有校验机制的问题,写性能相对不高。
-
④可靠性高,允许坏1块盘,不影响所有数据。
-
是由RAID3改进来的,但是RAID5模式是每块硬盘上分出一点空间来做数据校验,这样就不怕校验盘损坏了,相对与RAID3更安全一些
6.RAID6
- 最少需要四块硬盘,优化了RAID5的校验方式,可以允许两块硬盘损坏
7.RAID 10
-
①N(偶数,N>=4)块盘两两镜像后,再组合成一个RAID 0。
-
②N/2磁盘利用率。
-
③N/2块盘同时写入,N块盘同时读取。
-
④性能高,可靠性高。
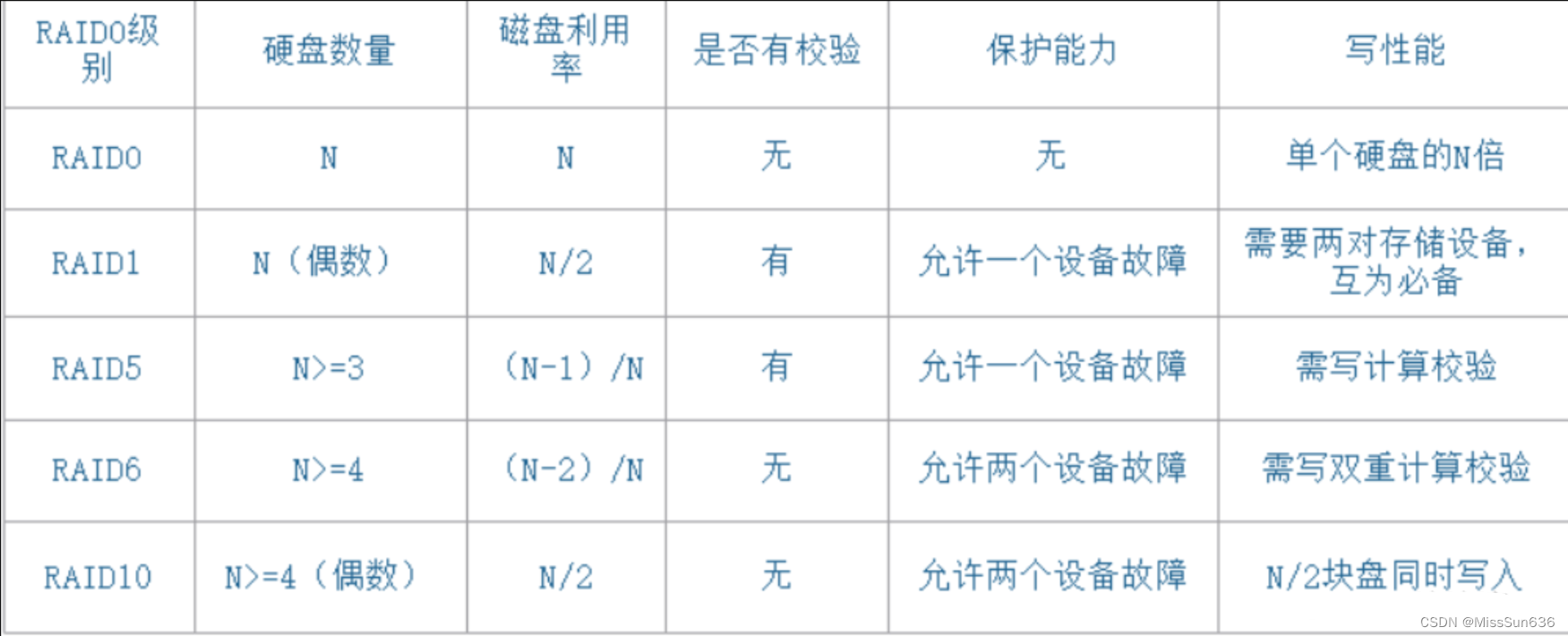
总结
- 如果只有两块硬盘建议组 RAID 1 ,三块硬盘建议组RAID 5 ,四块硬盘以上建议组RAID6
阵列卡介绍
-
①阵列卡是用来实现RAID功能的板卡。
-
②通常是由I/O处理器、硬盘控制器、硬盘连接器和缓存等一系列组件构成的。
-
③不同的RAID卡支持的RAID功能不同。
-
例如支持RAIDO、RAID1、RAID5、RAID10等。
-
④RAID卡的接口类型。
-
IDE接口、SCSI接口、SATA接口和SAS接口。
