redis 优化编码之字符串
### 字符串优化
字符串对象是redis内部最常用的数据类型。
- 所有的键是字符串对象
- 值对象除了整数之外都是使用字符串存储
lpush cache:type "redis" "tair" "memcache" "leveldb"
创建如上一个链表 需要创建一个链表对象和四个字符串对象。至少需要五个字符串对象。
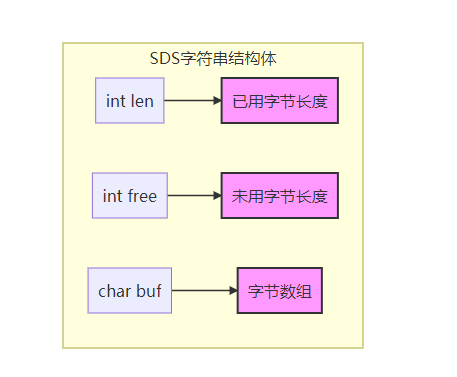
字符串结构
redis为采用原生C语言类型的字符串结构,拥有自己的字符串结构 ----内部简单动态字符串(simple dynamic string , SDS)