安全联盟可信任网站认证 网站中国十大电商公司排名
文章目录
- 更方便的部署方式
- 安装插件
- 使用插件
- 验证程序
- 常见访问出错的解决方案
- 404错误
- 405错误
- 500错误
- 空白页面
- 无法访问此网站
在文章 Tomcat+Servlet初识中,我们通过七个大的步骤才可以完成一个简单的Servlet程序,这个过程无疑是非常繁琐的,那么我们有没有什么办法可以适当的简化这样一个流程呢?答案当然是肯定的,首先一劳永逸的方法自然就是java提供给我们的SpringBoot框架,关于框架的知识我们将在后面慢慢了解,这里我们就尝试借助一些简单的插件来完成我们的需求~
更方便的部署方式
安装插件
我们的整个流程共有七大步,除去我们创建项目的前三步以及编写代码的第四步,我们可以简化的就是打包程序加部署程序的五六步,我们可以借助IDEA的一个插件来完成;
插件的安装流程如下:
点击File->Settings ;
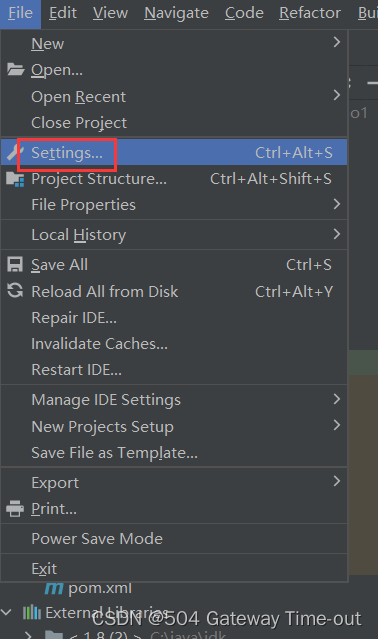
来到如下所示的界面,点击Plugins后在输入框中输入smart tomcat,就可以看到需要安装的插件 ;

下面是安装成功的界面 ;
这里安装smart tomcat插件的功能,主要就是可以直接在idea中调用tomcat,也就省去了我们打包程序和将程序部署到tomcat目录中去的这样一个过程;
使用插件
具体的使用流程如下:
点击这里的Add按钮;

点击+号,选择我们安装好的smart tomcat插件;
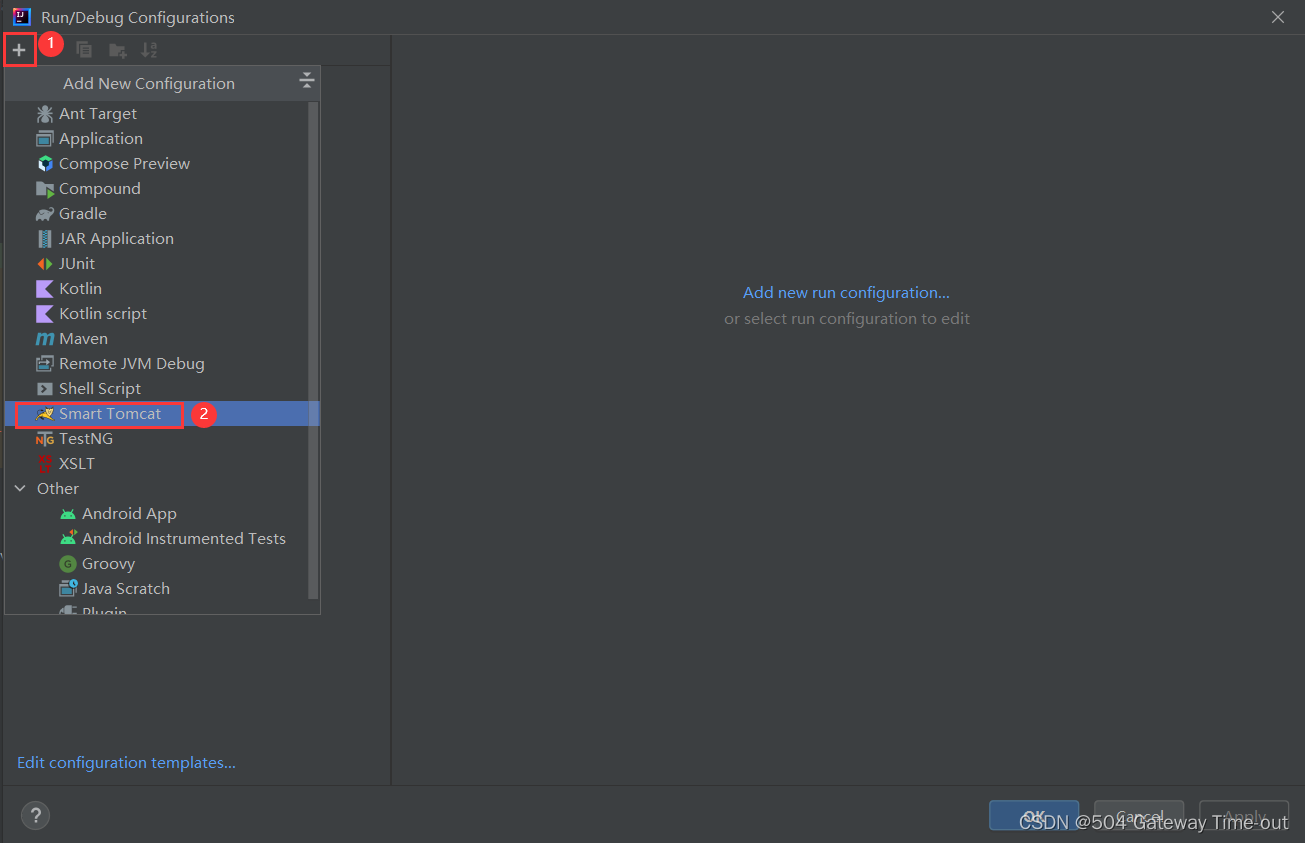
进行相关配置;
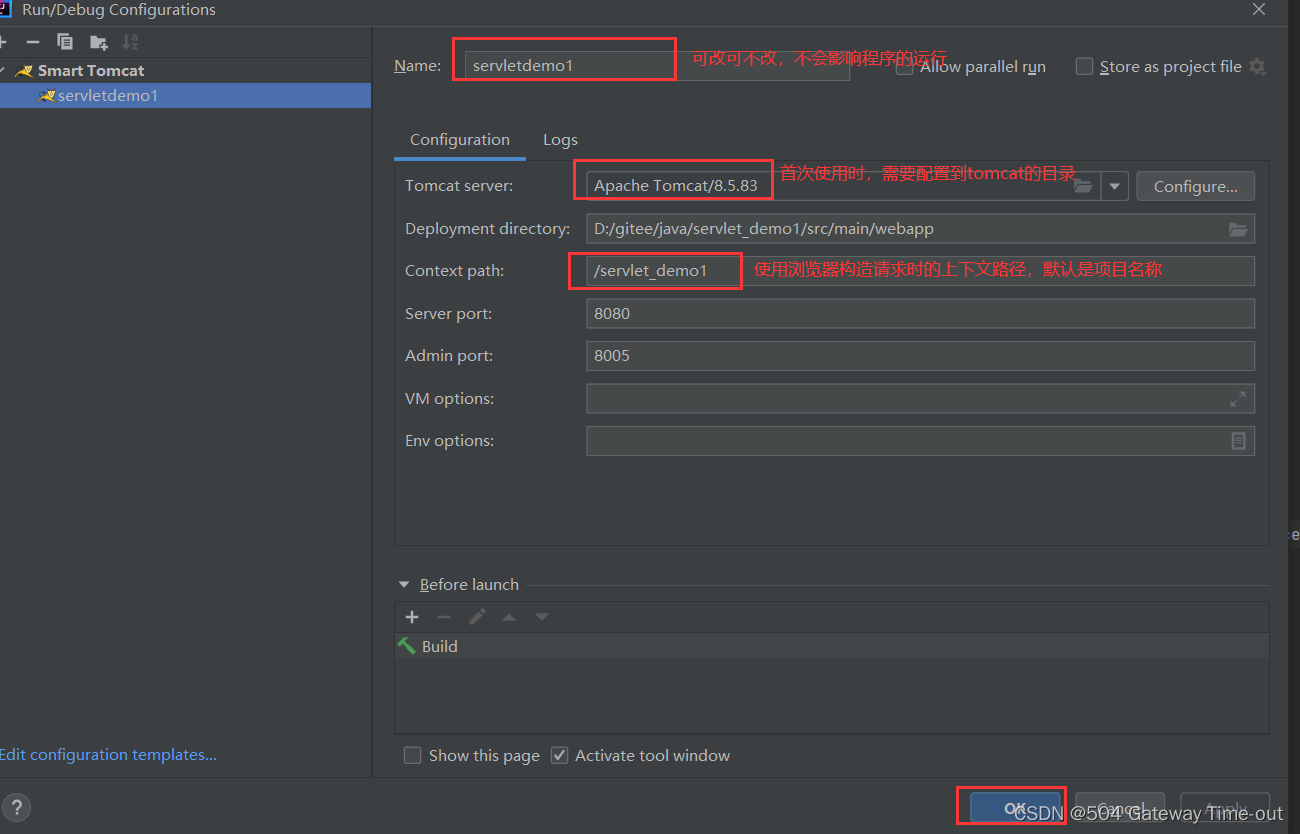
上述操作顺利完成之后,之前的Add按钮处就会如下显示:
然后,我们就可以使用插件,在IDEA中直接调用tomcat了;
验证程序
点击程序启动按钮(绿色的小三角)即可~
控制台有如下显示时,就表示tomcat启动成功:
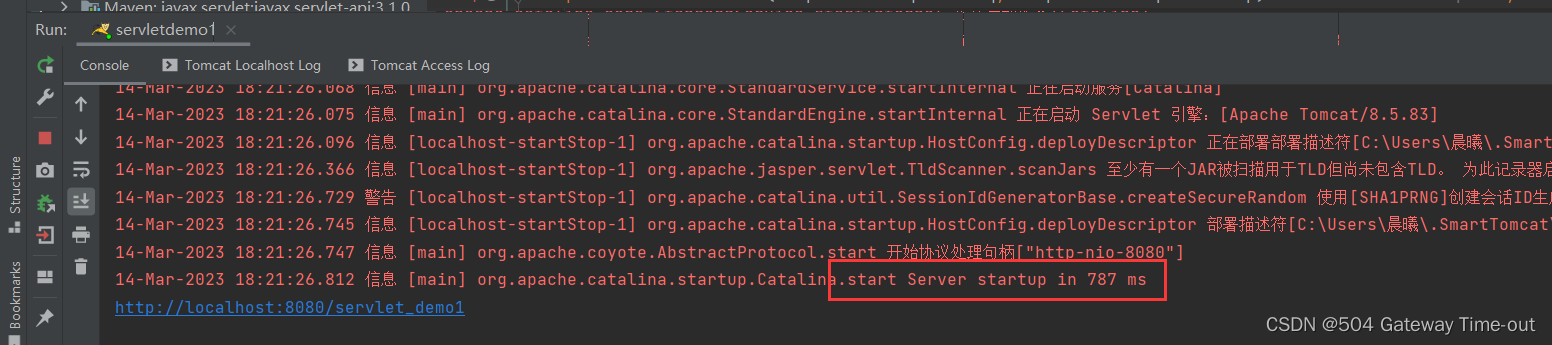
在浏览器中构造请求,验证程序:
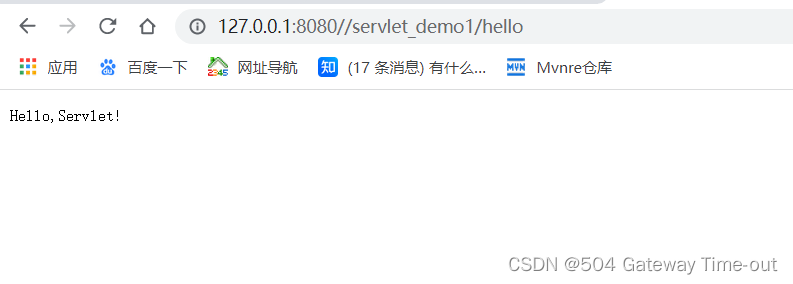
请求路径中的servlet_demo1就是前面配置时的Context Path,hello就是代码中注解的内容~
这样,我们每次修改代码之后,就不再需要重复地进行打包部署的操作,而是直接重新在idea中启动程序即可~
常见访问出错的解决方案
在使用浏览器构造请求时,可能稍不注意就会访问出错,得不到我们想要的结果,下面是一些常见的错误以及解决方法;
404错误
表示用户访问的资源不存在,大概率是请求路径的问题;
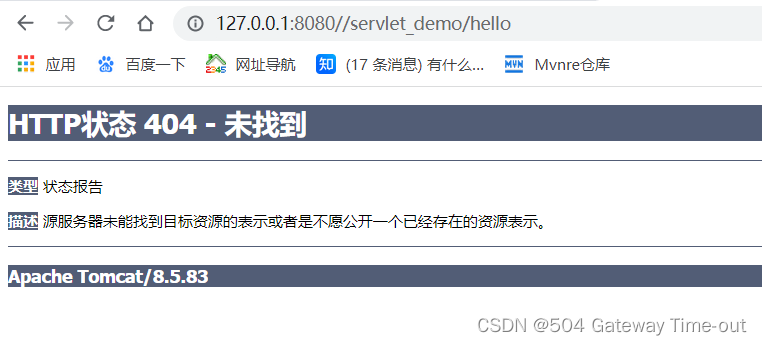
排查思路:
- 检查路径中Context Path与配置中的Context Path是否一致;
- 检查路径中servlet Path与程序中注解的内容是否对应;
- web.xml中的内容有误,检查其中的内容;
出现404的主要原因还是请求的路径有误,可以着重排查相关部分;
405错误
405错误一般指指定的请求方法不能被用于请求响应的资源,简单来说就是HTTP请求方法没有正确实现;
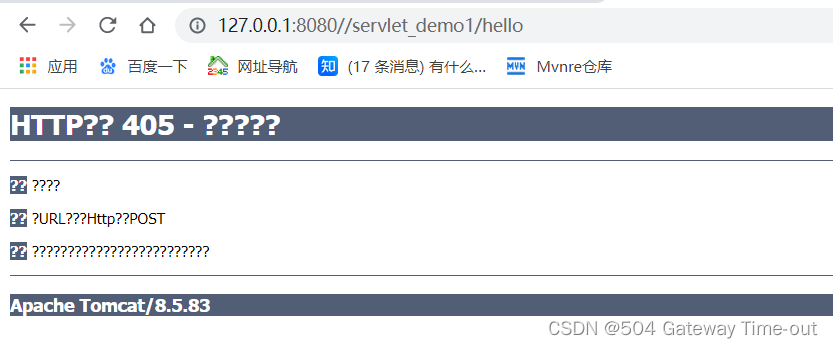
排查思路:
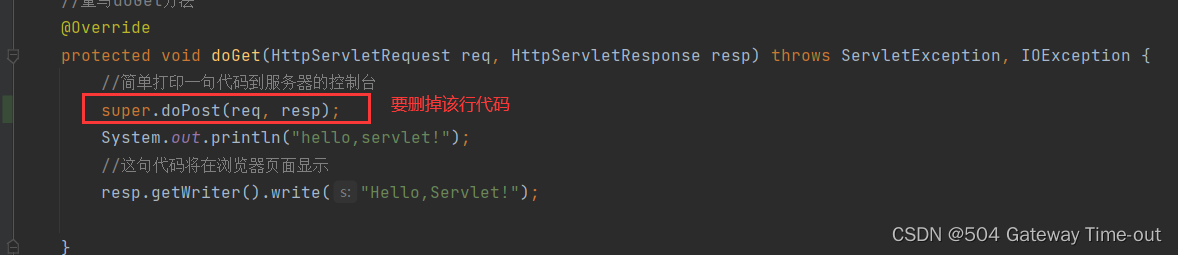
- 检查代码中是否实现了相关方法(doGet/doPost);
- 代码正确实现,但没有删掉自带的调用父类方法的代码;
500错误
500错误表示服务器内部错误,一般是代码抛出异常带来的错误;
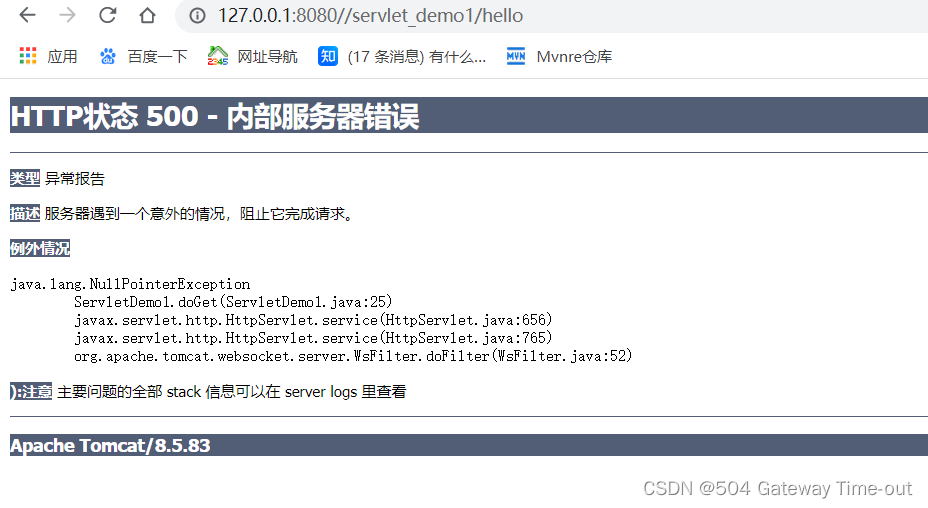
大概率是代码执行错误,程序抛出了异常,可以根据提示的错误信息检查代码逻辑~
空白页面
大概率是没有调用或者没有正确调用write()方法,返回的请求中body中数据为空~
无法访问此网站
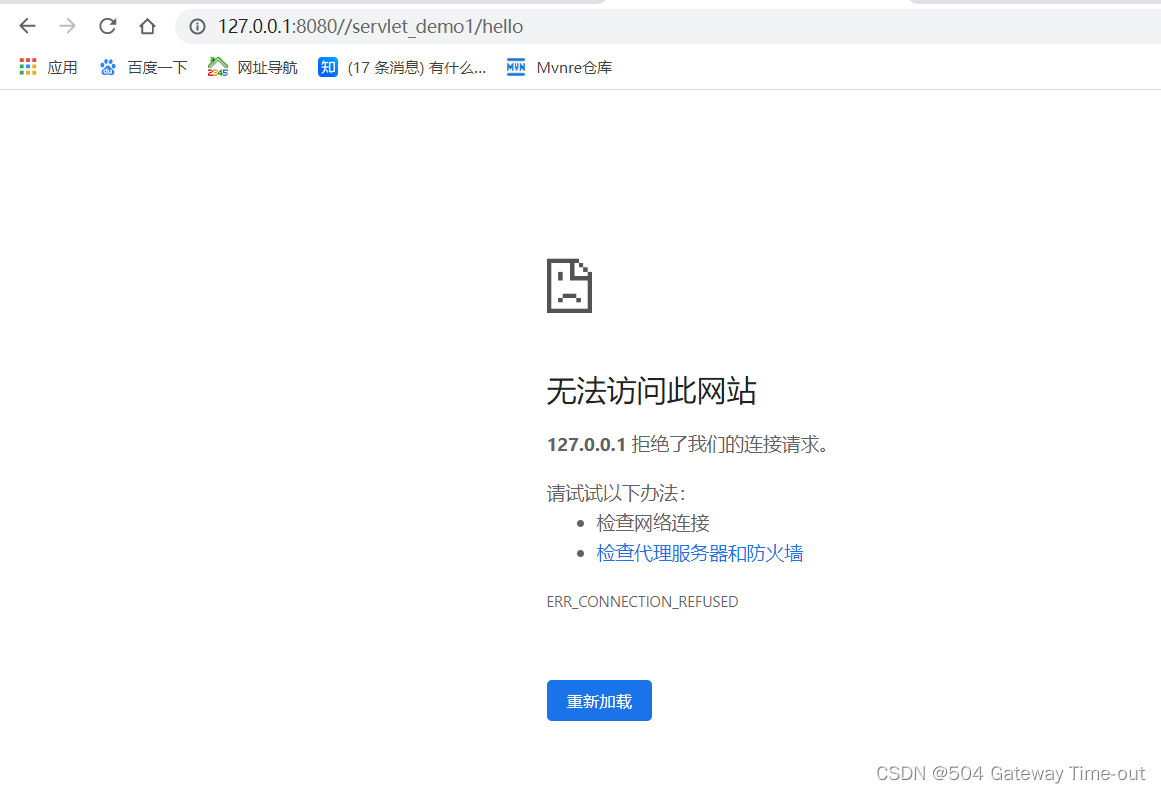
大概率是tomcat没有启动成功~
编写servlet程序容易出现的错误大致就是以上这些啦,可以根据实际情况结合日志以及抓包结果具体分析,希望我们的程序执行顺利,生活也顺利吖~
over!
